getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie

Для наблюдений y(Ti) из (3.2.3), в соответствии с (3.2.6), сформируем локальные функционалы S(cj , y j ) :

yM(cj , Ti) сводится к задаче минимизации локальных функциона-

Минимизация квадратичных функционалов S(cj , y j ) реализу-

ется по схеме, которая была предложена в разд. 2.4. С этой целью были сформированы соответствующие локальные базисные функ-

Введѐм локальные векторы сигналов y j (Ti) размерности (N, 1),

соответствующие локальному интервалу с номером j

yj (Ti) y(i N( j 1)), i 0, 1,..., N 1, j 1,..., m.

С использованием локальных векторов сигналов и локальных базисных функций вычислим локальные коэффициенты Фурье

с помощью которых находим оптимальные параметры с1j , c2 j локальных моделей для аддитивной трендовой функции

Оценка трендовой функции p2 (Ti) может быть представлена в виде суммы модельных локальных оценок yM(cj , Ti)

91

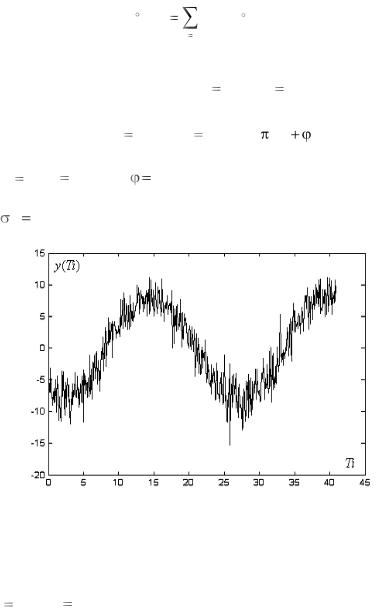
Проиллюстрируем результаты с помощью вычислений на математических моделях нестационарных сигналов. Сформируем сигнал

реализация модельных наблюдений нестационарного сигнала (3.2.5)

Рис. 3.2.3. Реализация модельных наблюдений нестационарного сигнала с аддитивной трендовой функцией

На рис. 3.2.4 изображена оценка трендовой функции в виде ку- сочно-линейных функций линии 1. Для вычисления оценки трендовой функции число локальных интервалов принято равным m 16 (N 32). Одновременно на этом же рисунке отмечена

пунктирной линией 2 модельная трендовая функция.

92

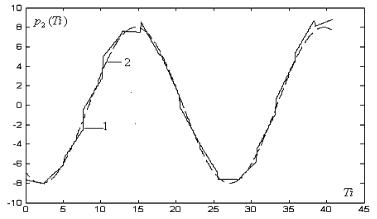
Рис. 3.2.4. Оценка аддитивной трендовой функции

3.3. Фильтрация аномальных значений в наблюдениях сигналов

3.3.1. Определение аномальных наблюдений сигналов

При решении некоторых задач ЦОС, например оценивания параметров моделей, могут возникать проблемы аномальных наблюдений. Присутствие аномальных значений в наблюдениях сигналов приводит к грубейшим погрешностям в оценках. Как правило, аномальные наблюдения имеют импульсный характер или представляются кратковременно действующими шумами большой интенсивности. Аномальные наблюдения возникают, в основном, вследствие внезапного нарушения структуры или параметров системы сбора данных.

Аномальные наблюдения определѐнным образом противопоставляются обычным наблюдениям. Предполагается, что аномальные и обычные наблюдения формируются на основе различных статистических механизмов. Следует отметить, что в практике ЦОС отсутствует общепринятое определение аномальных наблю-

дений. Так, отдельные наблюдения, которые резко выделяются по своим значениям среди ряда обычных наблюдений, можно опреде-

лить как аномальные. Бывают, как аномально большие, так и аномально малые наблюдения. Необходимо подчеркнуть, что данное определение является в значительной степени качественным и его

93

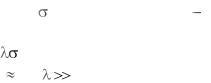
уточнение может быть осуществлено с помощью использования математических моделей возникновения аномальных наблюдений.

Рассмотрим частные примеры возникновения аномальных наблюдений. Первый пример связан с предметной областью экспертного анализа. Экспертные оценки эффективности некоторых сложных систем, выставляемых коллективом из нескольких экспертов, формируются в конечную последовательность и могут интерпретироваться как произведѐнные наблюдения эффективности. В основном, значения экспертных оценок группируются вблизи некоторого среднего с небольшим разбросом. Однако вполне возможны ситуации, когда кто-либо из экспертов по ряду причин выставляет экспертную оценку, сильно уклоняющуюся от среднего в сторону завышения или занижения. В этом случае, очевидно, последовательность таких оценок будет содержать видимые на глаз аномальные значения. Второй пример связан с предметной областью радиолокационных измерений координат движущихся объектов. Достаточно часто радиолокационные измерения происходят в условиях применения специально организованных помеховых воздействий, имеющих шумовой характер и препятствующих процессу измерения. В наблюдения координат под действием помех вносятся большие погрешности, катастрофически искажающие информацию – наблюдения становятся аномальными.

Модель статистического механизма возникновения аномальных наблюдений в значительной степени зависит от устройства конкретной системы сбора данных. Как правило, эта модель никогда не бывает точно известной, и может быть описана только приближенно, на основе дополнительных гипотез.

Разберѐм пример упрощенного модельного статистического механизма возникновения аномальных наблюдений. Пусть для дискретного момента с номером i формируется погрешность наблюдения w(i). С вероятностью q датчик случайных чисел вырабатывает числа w(i), которые подчиняются нормальному закону распределения с параметрами 2) и с вероятностью 1 q вырабатывает

числа w(i), подчиняющиеся нормальному закону распределения с

ся редкими и значительными по величине. Для q = 1 погрешности w(i) становятся обычными гауссовыми.

94

Рассматриваемый механизм формирования аномальных наблюдений может быть промоделирован, и наблюдения представятся следующим образом:

модельная последовательность y(i), состоящая из обычных и воз-

никающих отдельных аномальных наблюдений в соответствии с механизмом (3.3.1).

Рис.3.3.1. Модельные аномальные наблюдения

Ставится задача разработки алгоритмов фильтрации (обнаружения и устранения) аномальных наблюдений. Здесь будут рассмотрены пороговые и медианные алгоритмы, которые применяются на этапах предварительной обработки сигналов.

3.3.2. Пороговые алгоритмы

Достаточно распространенная группа методов фильтрации аномальных наблюдений базируется на применении пороговых алгоритмов. Пусть задана последовательность наблюдений y(i),

i 1,..., N, с возникающими отдельными (редкими) аномальными наблюдениями.

В простейшем варианте порогового алгоритма фильтрации аномальных наблюдений вычисляются скользящие оценки математи-

95

ческого ожидания и дисперсии с временным окном шириной k для i k, k 1,..., N :

который сравнивается с некоторым числом R, так называемым порогом. Достаточно часто имеет место R (2 3) (i). Если ri R, то принимается решение, что соответствующее этому номеру наблюдение y(i) относится к обычным; если ri R, то считается, что наблюдение y(i) относится к аномальным и удаляется из по-

следовательности (отбраковывается).

Описанный алгоритм, естественно, не свободен от недостатков. Он работает надѐжно для случая редких аномальных наблюдений. Эффективность порогового алгоритма зависит от назначаемого порога R : при малых значениях порога возможны ложные срабатывания – некоторые наблюдения могут приниматься за аномальные; при завышенных значениях порога возможен пропуск аномальных наблюдений.

Данный вариант порогового алгоритма должен рассматриваться всего лишь как основа для реального порогового алгоритма фильтрации аномальных наблюдений. Точная настройка пороговых алгоритмов зависит от дополнительной априорной информации.

3.3.3. Медианные фильтры

Алгоритмы фильтрации (обнаружения и устранения) аномальных наблюдений, основанные на использовании медианной фильтрации, широко применяются в многочисленных приложениях ЦОС.

Рассмотрим простейший вариант алгоритма медианного

Подвергнем элементы этой последовательности преобразованию упорядочения U( , ,..., ): образуем из элементов исходной после-

96

довательности новую последовательность, в которой элементы переставлены в порядке возрастания или убывания:

Выберем среднее по номеру в новой последовательности, которое имеет фиксированное обозначение y(n). Результатом работы ме-

дианного фильтра для последовательности y(1), y(2),..., y(k) является определѐнная выше величина y(n) :

y(n) Med (y(1), y(2),..., y(k)). .

Медианная фильтрация может реализовываться с помощью временного окна шириной k, скользящего по исходной последова-

Видно, что первые и последние n точек в отфильтрованной последовательности отбрасываются.

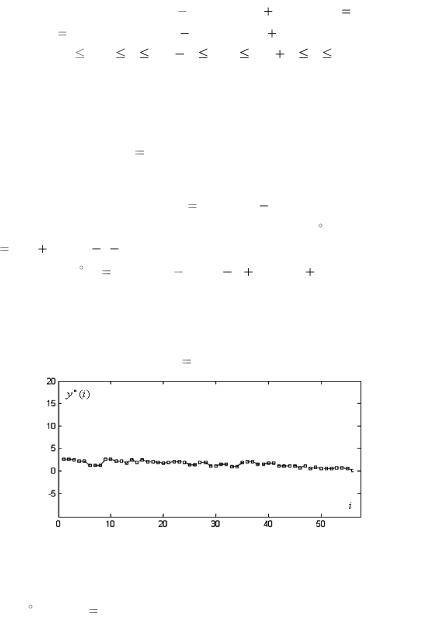
Для аномальных наблюдений, представленных на рис. 3.3.1, применена медианная фильтрация. Работа медианного фильтра с временным окном шириной k 3 проиллюстрирована на рис. 3.3.2.

Рис. 3.3.2. Результаты медианной фильтрации аномальных наблюдений

В табл. 3.3.1 помещена реализация y(i) с аномальными наблююдениями и соответствующие результаты медианной фильтра-

ции y (i) для i 2,..., 25.

97

Таблица 3.3.1

данный медианный фильтр обнаруживает и устраняет аномальные наблюдения.

В медианных фильтрах реализуется нелинейная обработка наблюдений. Применение медианной фильтрации в ряде случаев оказывается более эффективным с точки зрения точности по сравнению с применением фильтров, основанных на линейной обработке наблюдений. Линейная обработка наблюдений является оптимальной по точности для гауссовых погрешностей и совершенно неудовлетворительной по точности для сигналов с аномальными наблюдениями. В случаях с аномальными наблюдениями медианные фильтры дают лучшую точность, чем традиционные линейные фильтры.

98

Специфическая особенность медианных фильтров состоит в их слабой чувствительности к наблюдениям, которые резко выделяются на фоне обычных наблюдений, что позволяет применять медианные фильтры для фильтрации аномальных наблюдений. Функционирование алгоритмов медианной фильтрации в малой степени зависит от законов распределения случайных погрешностей, входящих в последовательность данных, подозрительных на наличие аномальных наблюдений.

Медианные фильтры обладают двумя основными достоинствами: 1) хорошим подавлением импульсных помех шириной менее половины временного окна; 2) хорошим пропусканием регулярных сигналов при малой ширине временного окна. Однако медианные фильтры по эффективности уступают линейным при подавлении обычных гауссовых погрешностей.

Повышение эффективности медианных фильтров может быть реализовано с помощью адаптивного изменения ширины временного окна в зависимости от характеристик шумовых погрешностей.

3.4.Дискретизация непрерывных сигналов. Теорема Котельникова

3.4.1.Дискретизация во времени и задача восстановления непрерывных сигналов

Положим, что задан исходный непрерывный сигнал y(t), t , который является в общем случае комплексным и определѐнным в бесконечных временных пределах. Для данного сигнала производится дискретизация во времени, где T – интервал дискретизации; y(Ti) – дискретные значения непрерывного сигна-

ла; fd 1 T – частота дискретизации, Гц; – круговая

частота дискретизации. При фиксированном временном интервале T, дискретизация осуществляется равномерно для моментов времени ti Ti. Дискретизация может производиться неравномерно для

произвольных моментов времени ti и еѐ результатом служит соответствующая последовательность дискретных значений непрерывного сигнала y(ti ). Здесь будем рассматривать только равномер-

ную дискретизацию во времени; пренебрежѐм погрешностями, возникающими из-за дискретизации по уровню.

99

Задача восстановления непрерывного сигнала y(t) по его дискретным значениям y(Ti) фактически представляет собой задачу интерполяции. Восстановление сигнала здесь состоит в том, что по

Пусть исходный сигнал y(t) принадлежит к некоторому задан-

ному классу функций; допустим, что можно подобрать, учитывая свойства этого заданного класса функций, соответствующие базисные функции i (t, T), t , i . Сформируем функ-

цию y(t, N), представляющую собой конечную взвешенную сумму базисных функций i (t, T) с весовыми коэффициентами y(Ti). В качестве восстановленного сигнала y (t) для y(t) примем предел

Задача восстановления может считаться успешно решѐнной, если будет выполнено равенство

Возможность восстановления сигнала по его дискретизованным значениям зависит от частотных свойств сигнала и выбранной частоты дискретизации. Высокая частота дискретизации, очевидно, позволит осуществить восстановление сигнала; для низкой частоты дискретизации восстановление в ряде случаев проблематично.

3.4.2. Появление «кажущихся» частот

Неправильно выбранная частота дискретизации, которая не согласована с частотными свойствами сигналов, приводит к появлению так называемых «кажущихся» частотных составляющих.

Разберѐм пример, в котором дискретизации подвергается непрерывный синусоидальный сигнал вида y(t) sin2 f0t с периодом

T0 1 f0 . На рис. 3.4.1 исходный сигнал y(t) изображен сплошной линией.

100