
getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie
.pdf
основе цифровой обработки зашумлѐнных сигналов x(t), y(t)
(4.4.12) на заданном интервале времени 0 |
t |
t f . |
|
||
Модель системы сигналов x(t), y(t) для многочастотного слу- |
|||||
чая описывается соотношениями |
|
|
|
|
|
|
L |
|
|
|
|
x(t) |
Е1l (t)cos |
1l (t) |
w1(t) , |
|
|
l |
1 |
|
|
|
|
L |
|
|
|
|
|
y(t) |
E2l (t)cos |
2l (t) |
w2 (t) . |
(4.4.13) |
|
l |
1 |
|
|
|
|
Вычисление оценок разностей фаз |
xy,l , l |
1,..., L, |
для частот- |
||
ных составляющих сигналов производится на основе цифровой обработки зашумлѐнных многочастотных сигналов x(t), y(t) (4.4.13)
на заданном интервале времени 0 t t f . |
|
Перейдѐм к дискретизованным сигналам x(i) |
x(Ti), |
y(i) y(Ti), которые определены в N точках, i 0, 1,..., N |
1. На- |
метим подход к оцениванию разностей фаз колебательных сигналов с использованием оценок функций ВСПМ. Пусть заданы два синусоидальных комплексных дискретизованных сигнала
|
|
x(i) |
A e j Wqi , |
y(i) |
A Wqi , |
i 0, 1,..., N |
1, |
(4.4.14) |
|||
|
|
|
|
|
1 |
|
2 |
|
|
|
|
где A , A – постоянные амплитуды; W |
e j2 / N ; |
T – интервал дис- |
|||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
кретизации; f |
– частота сигналов; q f /(1/NT)), |
q |
q0 |
q, q0 – |
|||||||
целое, |
|
q |
|
1. Очевидно, разность фаз между сигналами x(i), y(i) |
|||||||
|
|
||||||||||
(4.4.14), по определению, |
xy |
. |
|
|
|
|
|||||
Найдѐм оценку функции ВСПМ для сигналов (4.4.14). Вычислим коэффициенты ДПФ cx (k), cy (k) cигналов x(i), y(i), пусть
с(k) – коэффициенты ДПФ для Wqi. Тогда очевидны соотношения,
вытекающие из (4.4.14), |
|
|
|
|
|
||
c (k) A e j |
c(k), c*(k) Ae j 1c*(k), |
c |
y |
(k) |
A c(k). |
||
x |
1 |
x |
1 |
|
|
2 |
|
На основе cx (k), cy (k) запишем выражения для оценки функции ВСПМ сигналов – оценки еѐ модуля и фазового угла
P (k) P A e |
j c*(k)A c(k), |
|
P (k) |
|
P A A |
|
c(k) |
|
2 |
, |
|
(k) |
. |
|
|
|
|
|
|
||||||||||
xy |
0 1 |
x 2 |
|
xy |
|
0 1 2 |
|
|
|
|
|
xy |
|
|
|
|
|
151 |
|
|
|
|
|
|
|
|
|
|
|

Заметим, что в данном частном случае для комплексных синусоидальных сигналов фазовый угол функции ВСПМ не зависит от ин-
декса k. Будем находить оценку искомой разности фаз |
xy |
из |
|
|
оценки фазового угла ВСПМ в точке координаты максимума модуля функции ВСПМ. В данном случае эта координата равна k q0:
q |
arg{max |
|
P (k) |
|
2}, |
xy |
xy |
(q ) . |
|
|
|||||||
0 |
k |
|
xy |
|
|
0 |
||
|
|
|
|
|
|
|
|
Продолжим рассмотрение задачи оценивания разности фаз, когда два синусоидальных комплексных сигнала аддитивно смешаны с шумами:
x(i) A e j Wqi |
w (i), |
y(i) |
A Wqi |
w (i), i 0, 1,..., N 1, |
(4.4.15) |
1 |
1 |
|
2 |
2 |
|
где w1(i), w2 (i) – шумовые комплексные последовательности независимых нормальных случайных чисел с нулевым математическим ожиданием и дисперсией 2.
Коэффициенты ДПФ для синусоид x(i), y(i) (4.4.15) запишутся с учѐтом аддитивности шумов:
|
|
с (k) A e j |
c(k) c (k), с (k) A e j c(k) c (k), |
||||
|
|
x |
1 |
w |
x |
1 |
w |
|
|
|
|
1 |
|
|
1 |
где |
сw |
(k), cw (k) – |
коэффициенты ДПФ для |
w1(i), w2 (i), i 0, |
|||
|
1 |
|
2 |
|
|
|
|
1,..., N |
1. |
Для точки k q0 |
и в еѐ окрестности, соответствующей |
||||
расположению максимума модуля функции ВСПМ, должны выполняться неравенства, при условии малых 2 :
сw (q0 ) |
|
A1c(q0 ) |
, |
сw (q0 ) |
|
A2c(q0 ) |
. |
1 |
|
|
|
2 |
|
|
|
Для оценки функции ВСПМ комплексных синусоидальных сигналов (4.4.15) оказываются справедливыми приближѐнные равенства с учѐтом малости шумов:
Р (q ) |
|
P A A |
|
c(q ) |
|
2 |
, |
xy |
xy |
(q ) . |
|
|
|
||||||||
xy 0 |
|
0 1 2 |
|
0 |
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
Алгоритм оценивания разностей фаз для системы синусоидальных сигналов в шумах на основе функций ВСПМ, таким образом, состоит из этапов: 1) вычисления оценки функции ВСПМ сигналов Pxy (k), k 0, 1,..., N 1 и еѐ составляющих – функции модуля
Pxy (k) и функции фазового угла xy (k); 2) вычислении координаты максимума функции модуля ВСПМ
152

q0 |
k , k arg{ max |
Pxy (k) |
}; |
|
k 0,1,...,N 1 |
|
|
3) вычислении оценки разности фаз по функции фазового угла ВСПМ xy xy (q0). Для повышения точности оценивания раз-
ности фаз на больших временных интервалах применяется процедура усреднения. Предложенный алгоритм может быть обобщѐн на случай многочастотных сигналов.
Рассмотрим численный пример моделирования предложенного алгоритма оценивания разности фаз для системы зашумлѐнных
двухчастотных сигналов. |
|
|
|
|
|
|
|
|
Смоделируем |
систему |
предлагаемых |
сигналов |
x(i) x(Ti), |
||||
y(i) y(Ti), определѐнных в N f точках, i |
0, 1,..., N f |
1, |
||||||
x(i) A cos(2 f Ti |
11 |
) |
A cos(2 |
f Ti |
12 |
) |
w (i), |
|
11 |
1 |
|
12 |
2 |
|
1 |
||
|
y(i) A211 cos(2 f1Ti |
21) |
|
|
|
|||
|
A22 cos(2 f2Ti |
22 ) w2 (i) . |
|
|
(4.4.16) |
|||
Для (4.4.16) дискретные шумы w1(i), w2 (i) моделируются независимыми нормальными числами с нулевыми математическими ожи-
даниями и дисперсиями |
2, |
2. Модельные сигналы (4.4.16) име- |
||||||||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
ют |
следующие |
исходные параметры: |
A |
1,0; |
A |
2,0, |
||||||
|
|
|
|
|
|
|
|
|
11 |
|
12 |
|
A21 |
4,5; |
A22 5,5, |
f1 |
10,0 Гц; |
f2 |
18 Гц , |
11 |
1,5; |
12 |
4,0, |
||
21 |
3,0; |
22 |
1,0; |
1 |
1,5; |
2 |
1,5. Разности фаз, приведѐнные |
|||||
|
|
|
|
|
|
|
|
|
||||
к диапазону 2 для частотной составляющей с частотой |
f1 , со- |
|||||||||||
ставляют величину |
12,1 |
11 |
21 |
4,78, для частоты |
f2 |
– ве- |
||||||
личину |
|
12,2 |
12 |
22 |
3,0. |
|
Интервал |
|
дискретизации |
|||
|
|
|
|
|
|
|
|
|
|
|||
T |
0,01 c, |
локальный интервал состоит из N |
512 точек, |
число |
||||||||
локальных интервалов m 32.
На рис. 4.4.1а представлен график оценки модуля функции ВСПМ модельных сигналов (4.4.16) для диапазона 0 k N / 4 1. Положение максимумов может быть оценено на основе визуально-
го |
анализа |
графика |
рис. 4.4.1а или, исходя из рассмотрений |
||
разд. 4.2.1, q01 k1 |
f1NT |
10 512 0,01 52. |
Оценки разностей |
||
фаз для составляющих сигнала c частотами |
f1, f2 определяются |
||||
из |
расчѐтов |
или графика |
рис. 4.4.1б и принимают значения |
||
|
|
|
|
153 |
|
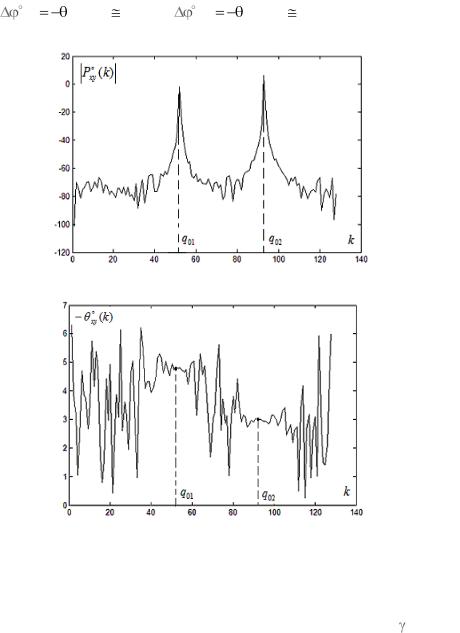
xy,1 |
xy (q01) 4,75, |
xy,2 |
xy (q02) 3,02, удовлетвори- |
тельно соответствующие исходным параметрам.
Рис.4.4.1а. Оценка модуля функции ВСПМ модельных сигналов (4.4.13)
Рис.4.4.1б. Оценка фазового угла функции ВСПМ модельных сигналов (4.4.13)
4.4.3.Применение функции ВСПМ для оценивания коэффициента когерентности колебательных сигналов
На основе ВСПМ вычисляется коэффициент когерентности xy , являющийся параметром, который служит мерой взаимосвязи двух
154

случайных сигналов x(t), y(t). Определим некоторые очевидные свойства, которыми может быть наделѐн вводимый коэффициент.
|
1. Коэффициент когерентности должен быть |
ограниченным: |
|||||||||||||||
0 |
|
xy |
1 (как один из вариантов определения). |
Если |
xy |
1, то |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
имеет |
место |
полная |
взаимосвязанность двух |
сигналов; |
если |
||||||||||||
|
xy |
0, |
то сигналы являются полностью несвязанными. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Очевидно, что для синусоидальных сигналов |
|
|
|
|
|
|||||||||||
|
|
|
y(t) |
A cos( |
t |
1 |
), |
x(t) |
A cos( t |
2 |
) |
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
||
коэффициент |
когерентности |
|
должен |
удовлетворять |
равенству |
||||||||||||
|
xy |
1. |
Для |
синусоидальных |
|
сигналов аддитивно смешанных с |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шумами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y(t) A cos( |
t |
1 |
) |
w (t), |
x(t) |
A cos( t |
2 |
) |
w (t) |
|
|||||
|
|
|
1 |
|
|
|
1 |
|
|
|
2 |
|
2 |
|
|
||
коэффициент когерентности должен быть меньше единицы |
xy |
1. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Естественно, что при увеличении интенсивности шумов коэффициент когерентности уменьшается.
3. Если два случайных сигнала статистически независимы, на-
пример x(t) w1(t), y(t) w2 (t), – |
независимые белые шумы, то |
|
должно выполняться соотношение |
xy |
0. |
|
|
|
4. Если два сигнала связаны некоторой линейной зависимостью, то, очевидно, xy 1.
Рассмотрим неравенство, позволяющее сделать обоснование для вводимого коэффициента когерентности:
с |
|
(k) c (k)e |
j |
yx (k) |
|
* |
* |
j yx (k) |
|
0. |
|
|
|
|
|||||||||
y |
|
|
|
с |
y |
(k) c (k)e |
|
|
|||
|
x |
|
|
|
|
x |
|
|
|
||
Сделаем соответствующее перемножение модулей, получим в качестве слагаемых выражения для оценок функций СПМ и ВСПМ:
2P (k) |
P (k)e j |
yx (k) |
P (k)e j |
xy (k) |
P (k) 0. |
yy |
yx |
|
xy |
|
xx |
Приведѐм соотношения, с помощью которых выведем основное неравенство, используемое для определения коэффициента когерентности:
P (k) |
|
P (k) |
|
e j yx (k) , P (k) |
|
|
P (k) |
|
e j yx (k) , |
||
|
|
|
|
||||||||
yx |
|
yx |
|
|
yx |
|
|
yx |
|
|
|
|
|
|
|
||||||||
|
|
2P (k) 2 |
P (k) |
P (k) 0. |
|||||||
|
|
yy |
|
|
yx |
|
xx |
||||
|
|
|
155 |
|
|
|
|
|
|
||

Последнее выражение можно рассматривать как квадратный полином от ; для обеспечения его положительности необходимо, чтобы его дискриминант был меньше нуля:
4 |
|
P (k) |
|
2 |
4P (k)P (k) 0, |
|
P (k) |
|
2 |
P (k)P (k). |
|
|
|
|
|||||||
|
|
xy |
|
|
xx yy |
|
xy |
|
|
xx yy |
Полученное неравенство ложится в основу эмпирического определения функции коэффициента когерентности, для которого
выполняется условие |
0 |
xy |
1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (k) |
|
2 |
|
|
|
|
|
|
|
|
||
|
|
xy (k) |
|
|
xy |
|
|
. |
|
|
|
|
|
|
|
||
|
|
|
Pxx (k)Pyy (k) |
|||||
|
|
|
|
|
||||
С использованием оценок функций СПМ и ВСПМ сигналов записывается оценка функции коэффициента когерентности в дискрет-
ных частотных точках |
k : |
|
|
|
|
||||||
xy ( |
k ) |
|
Pxy ( |
k ) |
|
2 |
, k |
2 |
k, |
k 0, 1,..., N 1. |
|
|
|
||||||||||
Pxx ( k )Pyy ( k ) |
NT |
||||||||||
|
|
|
|
|
|||||||
Рассмотрим вычисление функции коэффициента когерентности
для комплексных синусоид без шумов. Положим x(i) A e j Wqi ,
1
y(i) A Wqi , |
c (k) |
A e j |
|
c(k), |
c |
(k) |
A c(k). |
|
Здесь c(k) – коэф- |
|||||||||
2 |
x |
1 |
|
|
|
|
|
|
y |
|
2 |
|
|
|
|
|
|
|
фициенты ДПФ для Wqi. Тогда |
|
|
|
|
|
|
|
|
|
|
||||||||
P (k) P c*(K)c |
(k) P A A e j c*(k)c (k), |
|||||||||||||||||
|
xy |
0 x |
|
y |
|
|
|
|
0 1 |
2 |
|
x |
|
x |
||||
|
|
P (k) |
|
2 P2 |
(A A )2 |
|
c(k) |
|
2 , |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
xy |
|
|
0 |
|
1 2 |
|
|
|
|
|
|
|
|
|||
|
P (k) P A2 |
|
c(k) |
|
2 , |
|
P (k) P A2 |
|
c(k) |
|
2 . |
|||||||
|
|
|
|
|
|
|||||||||||||
|
xx |
0 1 |
|
|
|
|
|
|
|
yy |
0 |
2 |
|
|
|
|
||
Видно, что для рассматриваемого примера имеет место равенство
xy |
1. |
Для комплексных синусоид с малыми шумами |
|||
|
|
|
|
|
|
|
|
x(i) A e j Wqi |
w (i), y(i) A Wqi |
w (i), |
|
|
|
1 |
1 |
2 |
2 |
запишем выражения для коэффициентов ДПФ
c (k) |
A e j |
x |
1 |
Для k q0 (k |
q0 ) |
A2c(q0 )
 cw2 (q0 ) ,
cw2 (q0 ) ,
индексов xy (k q0 )
c(k) cw (k), cy (k) A2c(k) cw (k). |
|
|
||
1 |
2 |
|
|
|
в предположении, что |
A1c(q0 ) |
|
cw (q0 ) |
, |
|
|
|
1 |
|
следует, что xy (k q0 ) 1, для остальных
0.
156

На основе системы модельных сигналов (4.4.16) произведены вычисления оценки функции коэффициента когерентности xy (k).
На рис. 4.4.2а приведѐн график оценки xy (k), соответствующий m 32; 1 1,5; 2 1,5, – расчѐтный пример 1.
Рис. 4.4.2а. Оценка коэффициента когерентности модельных сигналов (4.4.16) – пример 1
На рис. 4.4.2б приведѐн график оценки xy (k), соответствующий m 32; 1 7,5; 2 7,5, – расчѐтный пример 2 с увеличен-
ной дисперсией шумов. На рис. 4.4.2в приведѐн график оценки xy (k) параметров m 64; 1 7,5; 2 7,5, – расчѐтный пример
3 с увеличенным числом локальных интервалов.
Рис.4.4.2б. Оценка коэффициента когерентности модельных сигналов (4.4.13) – пример 2
157
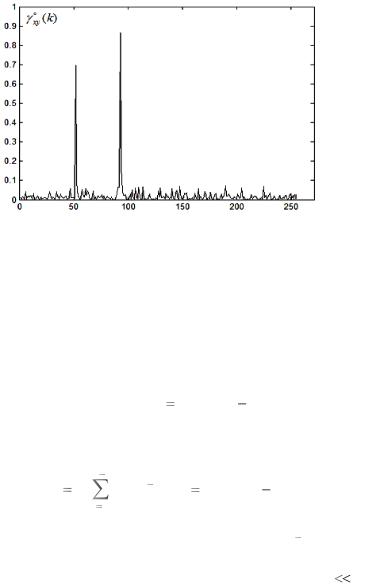
Рис.4.4.2в. Оценка коэффициента когерентности модельных сигналов (4.4.13) – пример 3
Введѐнная эмпирическим путѐм функция коэффициента когерентности является чувствительным индикатором наличия связей между сигналами.
4.5. Алгоритм быстрого преобразования Фурье
Оценим временные затраты, необходимые для вычисления коэффициентов дискретного преобразования Фурье (ДПФ) для последовательности данных y(i), i 0, 1,..., N 1, непосредственно
по формулам из определения. Запишем ещѐ раз выражение для прямого ДПФ, включающее в себя операции сложения, умножения и вычисления тригонометрических функций:
|
1 |
N 1 |
c(k) |
|
y(i)W ki , k 0, 1,..., N 1. |
|
||
|
N i 0 |
|
Если предположить, что в памяти ЭВМ заранее сформирована таблица значений базисных синусоидальных функций W ki , а также справедливо соотношение для времени выполнения операций комплексного сложения tc и умножения ty в виде неравенства tc ty ,
то время вычисления N комплексных коэффициентов ДПФ приближѐнно оценивается по формуле
158

T |
N2t |
y |
. |
(4.5.1) |
ДПФ |
|
|
|
Временные затраты вычисления коэффициентов дискретного преобразования Фурье на основании определения растут пропорцио-
нально N2 и для больших N составляют значительную величину.
Предлагаемый алгоритм быстрого преобразования Фурье (БПФ) обеспечивает существенное снижение временных затрат вычис-
ления коэффициентов ДПФ. Однако применение этого алгоритма возможно только для некоторых значений N; здесь будет рассмот-
рен вариант алгоритма БПФ для N 2r – числа наблюдений, равного целой степени двойки. В основе предлагаемого алгоритма БПФ лежит возможность сведения вычисления ДПФ для N чисел к вычислению двух ДПФ для N 2 чисел с проведением дополни-
2 чисел с проведением дополни-
тельных операций умножения.
Рассмотрим снова выражение для вычисления коэффициентов ДПФ; опустим для дальнейших удобств выкладок множитель 1 N , который можно будет учесть на последнем шаге:
N 1 |
|
|
|
|
c(k) |
y(i)W ki , |
k |
0, 1,..., N |
1. |
i |
0 |
|
|
|
Разобьѐм последовательность y(i), |
i |
0, 1,..., N |
1, на две подпос- |
|
ледовательности с чѐтными и нечѐтными номерами входных данных:
g(s) y(2s), h(s) y(2s 1), s 0, 1,..., N 2 1.
2 1.
Коэффициенты ДПФ исходной последовательности могут быть
записаны в виде двух сумм, |
k |
|
0, 1,..., N |
1: |
|
|
|
|
|
|
||||||
|
N /2 1 |
|
|
2 |
|
|
|
N /2 1 |
|
2 |
|
|
|
|
|
|
|
|
g(s)e |
j |
|
|
k 2s |
|
|
h(s)e j |
|
k(2s 1). |
|
||||
с(k) |
|
N |
|
|
N |
|
||||||||||
|
s 0 |
|
|
|
|
|
|
|
s 0 |
|
|
|
|
|
|
|
Сформируем указанные суммы в виде ДПФ размерности N 2: |
||||||||||||||||
N /2 1 |
|
j |
2 |
|
ks |
|
j 2 k |
N /2 1 |
|
|
j |
2 |
ks |
|
||
|
|
|
|
|
|
|
|
|||||||||
с(k) |
g(s)e |
|
N /2 |
|
|
e |
N |
h(s)e |
|
N /2 |
|
. |
||||
s |
0 |
|
|
|
|
|
|
|
|
s 0 |
|
|
|
|
|
|
Обозначим коэффициенты ДПФ cg (k), ch (k) для введѐнных чѐтных и нечѐтных подпоследовательностей:
159

|
|
N /2 1 |
2 |
|
|
N /2 1 |
2 |
|
|||||
с (k) |
|
|
g(s)e |
j |
|
ks , с (k) |
|
h(s)e j |
|
ks , |
|||
|
|
N /2 |
|
N /2 |
|||||||||
g |
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
s |
0 |
|
|
|
|
s |
0 |
|
|
|
|
|
|
|
k |
0, 1,...., |
N 2 1. |
|
|
|
|
|||
Запишем, |
введя |
множитель |
W k , |
первые N/2 коэффициентов |
|||||||||
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
ДПФ с(k) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e j |
2 |
|
|
|
|
|
|
|
|
|
|
|
W k |
N , |
с(k) c (k) |
W |
kc (k), |
k |
0, 1,..., N/2 1. |
|||||||
N |
|
|
|
|
g |
N |
h |
|
|
|
|
||
Eсли осуществить сдвиг индекса k на N/2, то оставшиеся коэффициенты ДПФ исходной последовательности с номерами от N/2 до
N/2 1 записываются аналогично: |
|
|
|
||
W (k N /2) |
W k , |
с(k N/2) |
c (k) |
W |
kc (k), |
N |
N |
|
g |
N |
h |
|
k |
0, 1,..., N/2 |
1. |
|
|
Из приведѐнного рассмотрения следует, что нахождение ДПФ для последовательности из N чисел свелось к вычислению двух ДПФ для двух подпоследовательностей из N/2 чисел и N/2 операций
комплексных умножений.
Вычисление ДПФ можно реализовать пошагово. На предпоследнем шаге можно осуществить переход к вычислению ДПФ для подпоследовательностей из N/2 чисел через ДПФ для подпосле-
довательностей из N/4 чисел и т.д. Общее число шагов подобного алгоритма составляет значение показателя степени двойки
r log2 N.
Проанализировав структуру формул алгоритма вычисления ДПФ из N чисел через вычисление ДПФ для подпоследовательностей из N/2 чисел, можно заметить, что алгоритм распадается на
последовательность однотипных подалгоритмов. Действительно,
выделим типовой подалгоритм |
|
|
|
||
с(k) c (k) |
W kc (k), с(k N/2) |
c (k) |
W |
kc (k), |
|
g |
N |
h |
g |
N |
h |
|
k |
0, 1,..., N/2 1. |
|
|
(4.5.2) |
Указанный подалгоритм называется «бабочка»; граф «бабочки» – схематическое изображение вычислительных операций, соответствующих (4.5.2) представлен на рис. 4.5.1.
160
