getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie

жет быть тем меньше, чем меньше рассматриваемый временной интервал. В случае, если требуется реализовать построение модели узкополосного сигнала на большом интервале времени, то в качестве такой модели может быть использована последовательность кусочно-синусоидальных модельных функций вида (2.3.4).

Возможно уточнение модели для узкополосного сигнала на малом интервале времени, учитывающее в сигнале частотную модуляцию. Примем модель yМ(c, Ti) в виде кусочно-синусоидальной

ние для модели линейно, частота и скорость частоты входят нелинейно.

Дальнейшее уточнение модели для узкополосного сигнала может быть реализовано на основе одновременного учѐта амплитудной и частотной модуляции. В этом случае примем модель yМ(c, Ti) в виде кусочно-синусоидальной функции с линейной

Иногда узкополосный сигнал может реализовываться в аддитивной смеси с низкочастотным трендом, природа которого бывает самой различной. В этом случае модель сигнала с трендом на ма-

на малом временном интервале представится в виде модельной ку- сочно-линейной функции d1

Для полигармонического сигнала, состоящего из суммы разночастотных узкополосных сигналов, на малом временном интервале для i 0, 1,..., N 1 возможно использование следующей модели

51

размерности (3L,1) . Амплитуды a1,..., aL, b1,..., bL входят в модель линейно, частоты 1,..., L нелинейно.

Следует отметить важный для дальнейших рассмотрений класс моделей сигналов, которые линейно зависят от вектора параметров

Для линейных по параметрам моделей должны быть введены базисные функции r (Ti), r 1,..., m, известного вида, зависящие от

дискретных аргументов. Модель (2.3.5) может быть представлена в виде скалярного произведения

Достаточно часто встречаются модели, линейные по части па-

m2,1 входит в модель нелинейно.

Отметим особо подкласс линейных моделей, для которых дискретные базисные функции являются ортогональными. По опреде-

лению, функции r (Ti) , r 1,..., m, составляют ортогональный базис для точек i 0,1,..., N 1, если выполняется условие

2.4. Оценивание параметров моделей сигналов

2.4.1. Оценивание параметров моделей как задача аппроксимации

Рассмотрим возможную постановку задачи оценивания параметрических модельных функций сигналов. Реализуем подход, свя-

занный с оптимальной аппроксимацией наблюдений сигналов.

Допустим, что имеется возможность замены параметрической

добранную модельную параметрическую функцию сигнала в виде функции известного вида f (c, t), зависящей от конечно-мерного

вектора параметров cT (c1,..., cm ). Будем считать, что функции f (c, t) принадлежат некоторому множеству F0, которое, в свою очередь, является подмножеством множества Р0:

ным введению ограничивающего множества для вектора парамет-

Из-за того, что вектор с является конечно-мерным, в общем случае оказывается невозможным осуществить замену p(t) на f (c, t)

с бесконечно малой погрешностью. Однако всегда можно подобрать такую функцию f (c, t), которая с некоторой заданной конеч-

ной точностью смогла бы заменить параметрическую функцию

В связи с условием (2.4.1) в качестве параметрической модели сигнала может быть принята функция вида

Примем, что функция наблюдения у(t), модель сигнала x( f (c, t), t) и погрешности наблюдений w(t) cвязаны соотношени-

ем

у(t) x( f (c, t), t) w(t).

Введѐм функционал S(c, y), являющийся мерой близости наблюдений у(t) и модельной функции x( f (c,t), t):

S(c, y) y(t) x( f (c,t), t).

Оценка p (t) исходной параметрической функции вследствие замкнутости R0m определяется на основе решения задачи опти-

мальной и аппроксимации наблюдений заданной моделью сигнала, сводящейся к применению нелинейного программирования

f (c, t) с удовлетворением условий (2.4.1), формированием соответствующей модели сигнала x( f (c, t), t) (2.4.2) и введению функционала S(c, y) предложена технология решения задачи получения оценок исходных параметрических функций p (t) на основе нели-

нейного программирования в задаче (2.4.3).

Поясним особенности выбора модельных параметрических функций f (c, t) на примере для нестационарного колебательного

сигнала x(t), рассматриваемого на некотором ограниченном ин-

тервале времени

x(t) E(t)cos (t).

Амплитудная и фазовая функции E(t), (t) служат в качестве параметрических функций для сигнала x(t), pT (t) (E(t), (t)), p1(t) E(t), p2(t) (t). Векторная параметрическая функция p(t) для сигнала имеет размерность (2, 1).

Положим, из априорных сведений, связанных с физическими особенностями сигнала и объекта, что сигнал x(t) имеет почти си-

нусоидальную амплитудную модуляцию и его несущая частота меняется почти линейно во времени. В этом случае параметрической функции p1(t) может быть поставлена в соответствие модельная

54

f (c, t) примет следующий вид

x( f (c, t)t) (c10 c11 sin(c12t c13))соs (c20 c21t c22t2 ) .

Рассмотрим возможную постановку задачи нахождения решения для задачи (2.4.3) – оценивания параметрических функций сигналов в дискретном случае.

Положим, что все переменные заданы в дискретные моменты времени Ti, i 0, 1,..., N 1, T – шаг дискретности по времени. От-

резок времени наблюдения (t0, t f ) определяется условиями: t0 0,

ванными нормально распределѐнными нормальными числами с нулевым математическим ожиданием и постоянной дисперсией. Функционал S(y, c) с учѐтом заданных свойств погрешностей за-

пишется в виде соотношения

приводит к задаче нелинейного программирования. Нахождение оптимального вектора параметров с позволяет построить оптимальную аппроксимационную модель x( f (c , t), t), оценку для па-

раметрической модельной функции и на еѐ основе определить оценку параметрической функции сигнала

55

c arg{ min S(у, c)}, p (Ti) f (c , Ti), i 0,1,..., N 1.

c R0m

2.4.2. Оценивание параметров линейных моделей для действительных сигналов

Рассмотрим решение задачи оценивания параметров линейных моделей для действительных сигналов. Пусть произведены наблю-

yM (c, Ti) cT (Ti).

Сформируем функционал S(c, y), являющийся мерой близости мо-

где Y – вектор наблюдений размерности (N,1); c – вектор параметров модели размерности (m, 1); X – матрица плана сигнала размерности (N, m). Нетрудно видеть, что разность для наблюдений и модели может быть сформирована в векторном виде

56

На основе введѐнных векторов и матриц функционал S(c, Y) запи-

сывается как скалярное произведение и представляет собой квадратичную форму

С учѐтом того, что имеет место равенство YT Xc cT XTY, можно записать

S(c, Y) YTY 2cT XTY cT XT Xc.

Нетрудно проверить, что для квадратичной формы S(c, Y) спра-

ведливо равенство

YTY 2cT XTY cT XT Xc YTY ((XT X) 1 XTY c)T (XT X ) ((XT X) 1 XTY c) YT X(XT X)XTY.

Очевидно, минимальное значение этой квадратичной формы достигается при

Последнее выражение может быть представлено в виде системы линейных уравнений

мерность (m, m); элементы этой матрицы симметричны относи-

тельно главной диагонали и определяются как скалярные произведения базисных функций

Нахождение оптимального вектора параметров c сводится к решению линейной системы уравнений

Dc b.

57

2.4.3. Оценивание параметров линейных моделей для комплексных сигналов

Рассмотрим решение задачи оценивания параметров линейных моделей для комплексных сигналов. Введѐм комплексные наблю-

пользованием суммы произведений сопряженных комплексных множителей

По аналогии с (2.4.5) введѐм комплексную разность функции наблюдения и модели Y(c) Y Xc. Воспользовавшись введѐнными

векторно-матричными переменными, но в комплексной форме, представим функционал S(Y, c) (2.4.8)

S(Y, c) Y*T (c) Y(c) (Y Xc)*Т (Y Xc).

С учѐтом равенства Y*T Xc c*T X*T Y запишем

S(Y, c) (Y Xc)*Т (Y Xc)

(2.4.9)

(Y* X *c*)T (Y Xc) Y*T Y 2Y*T Xc c*T X *T Xc.

Очевидно, справедливо равенство

Y*T Y 2Y*T Xc c*T X*T Xc Y*Т Y ((X*Т X ) 1 X*Т Y c*)T

(X*Т X) ((X*Т X) 1 X*Т Y c) YT X*(X*T X ) 1 X*T Y.

Минимальное значение этой квадратичной формы (2.4.9) достигается при

Оценка с из (2.4.10) может быть найдена с помощью решения системы линейных уравнений

58

Коэффициенты вектора b (коэффициенты Фурье) вычисляются в

Если базисные функции ортогональны, то нахождение параметров модели упрощается. Матрица D будет диагональной с элементами

drr r2 , r 1,..., m, drs 0, r s.

Оптимальные параметры модели выразятся через коэффициенты Фурье

2.5. Модели сигналов на основе рядов Фурье. Интеграл Фурье

2.5.1. Модели сигналов на основе действительного ряда Фурье

Рассмотрим построение моделей сигналов на основе действительного ряда Фурье.

Пусть наблюдения cигнала заданы в виде действительной функции y(t) на конечном интервале времени 0 t T0. Рассмот-

рим варианты условий сходимости рядов Фурье для y(t) . Первый вариант: если в некотором промежутке (t0 h, t0 h) с центром в точке t0 функция y(t) имеет ограниченное изменение, то еѐ ряд

Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 3. М.: Физматгиз. 1963. 656 с.

59

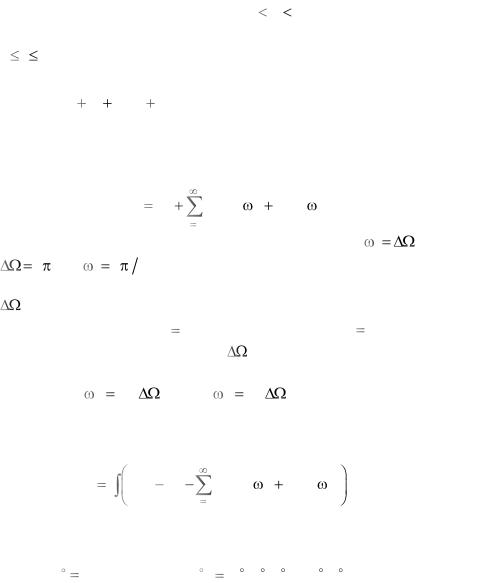
Фурье в указанном интервале для t0, 0 t0 T0, сходится к y(t0). Второй вариант: если функция y(t), определѐнная на интервале 0 t T0, имеет на нѐм не более чем конечное число точек разрыва, еѐ ряд Фурье в точке непрерывности t0 сходится к y(t0 ) или к сумме (y(t0 0) y(t0 0))/2 в каждой точке разрыва t0. Будем полагать, что для рассматриваемого сигнала y(t) выполнены

сформулированные условия сходимости.

Выбирается модель для указанного сигнала в форме действи-

дения, модельные синусоиды располагаются с шагом по частоте , который зависит от Т0. Вектор параметров модели имеет бес-

вале времени Т0 укладывает целое число периодов базисных

Нахождение вектора параметров модели сводится к минимизации указанного функционала, который, очевидно, является квадратичным по с:

Ограничимся конечным числом синусоид, составляющих модель, равным L. В этом случае вектор базисных функций для моде-

60