
getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie
.pdf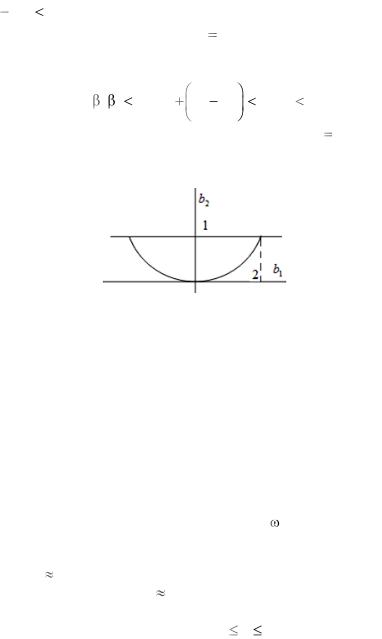
b2 |
4b 0. На рис. 6.2.2 на плоскости (b , b ) область таких па- |
|||
1 |
2 |
|
1 |
2 |
раметров лежит выше параболы b |
b2 |
/4. Чтобы полюса распола- |
||
|
2 |
1 |
|
|
гались внутри единичной окружности, необходимо выполнение неравенства
|
b2 |
|
b2 |
|
|
|
|
0 1 1, |
1 |
b2 |
1 |
1, |
b2 |
1, |
|
4 |
4 |
||||||
|
|
|
|
|
что соответствует области, лежащей ниже прямой b2 1. Параметры на плоскости (b1, b2 ), лежащие внутри луночки, обеспечивают устойчивость рассматриваемого цифрового резонатора.
Рис. 6.2.2. Область устойчивости цифрового резонатора
6.3. Задачи синтеза ЦФ
6.3.1. Классификация фильтров по типу АЧХ
Как правило, построение ЦФ начинается с выбора варианта синтезируемой передаточной функции (варианта амплитудно-фазо- частотной характеристики). Для решения этой части задачи синтеза целесообразно рассмотреть достаточно часто встречающуюся классификацию фильтров по типу АЧХ. Приведѐнные здесь варианты АЧХ являются функциями, которые зависят от нормированных цифровых частот w; разумеется, представленные АЧХ могут быть рассмотрены как функции аналоговых частот .
Низкочастотные фильтры (lowpass-фильтры) реализуют функцию пропускания сигналов с низкими частотами с коэффициентом усиления 1 и непропускания сигналов с высокими частотами с коэффициентом усиления 0. Общий вид функций АЧХ таких
|
, |
|
|
фильтров, обозначаемых как |
H1(w) |
в зависимости от нормиро- |
|
ванной частоты для диапазона 0 |
w 0,5, представлен на |
||
рис. 6.3.1а. |
|
||
191 |
|
|
|
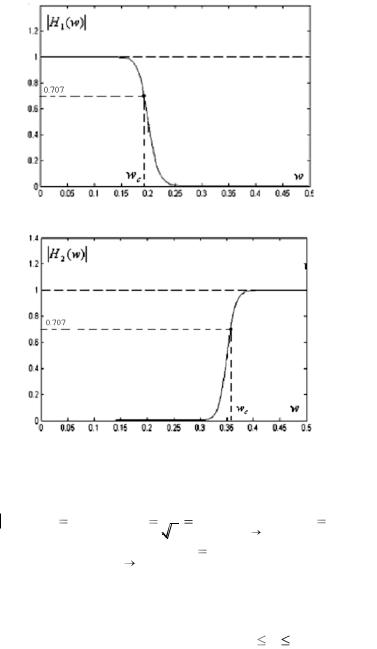
Рис. 6.3.1а. АЧХ для низкочастотных фильтров
Рис. 6.3.1б. АЧХ для высокочастотных фильтров
Для АЧХ таких фильтров могут быть справедливы следующие соотношения:
H (w ) |
|
2 |
1 , |
|
H (w ) |
|
1 |
|
0,707, |
lim |
|
H (w) |
|
1, |
|||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
1 c |
|
|
2 |
|
1 |
с |
|
2 |
|
|
|
w 0 |
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
H1(w) |
|
0, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
w |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где wс – нормированная частота среза
АЧХ рассматриваемых фильтров отличаются крутизной в окрестности wс (рис. 6.3.1б); так, для рис. 6.3.1а уменьшение АЧХ от единицы до нуля происходит в диапазоне 0,15 w 0,25, для слу-
192
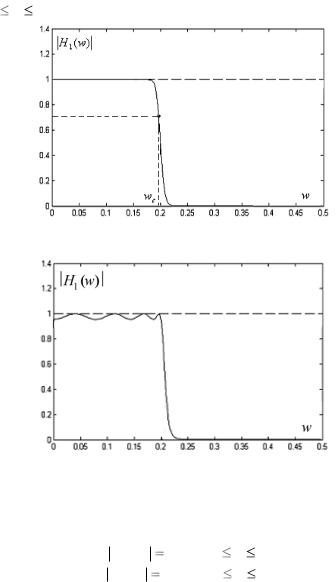
чая рис. 6.3.1в уменьшение АЧХ происходит в диапазоне
0,18 w 0,22.
Рис. 6.3.1в. АЧХ для низкочастотных фильтров с увеличенной крутизной
Рис. 6.3.1г. АЧХ с колебаниями для низкочастотных фильтров
Во втором случае АЧХ имеет большую крутизну, чем в первом. Идеальная АЧХ для низкочастотного фильтра удовлетворяет соотношениям
H1(w) 1 для 0 w w0, H1(w) 0 для w0 w 0,5,
где w0 – граничная частота, определяющая полосу пропускания.
Для некоторых типов фильтров функции АЧХ (низкочастотные и др.) допускают колебания (рис. 6.3.1г).
193
Высокочастоные фильтры (highpass-фильтры) пропускают сигналы с высокими частотами и не пропускают сигналы с низкими частотами. Общий вид АЧХ таких фильтров, обозначаемых в виде функции H2 (w) , зависящей от нормированной частоты в диапа-
зоне 0 w 0,5, изображѐн на рис. 6.3.1б. По аналогии с низкочастотными фильтрами, запишем
|
|
|
|
lim |
|
H2 (w) |
|
1. |
|
H2 |
(wc ) |
0,707; lim |
H2 (w) |
0; |
|
|
|||
|
|
w 0 |
|
|
w 0,5 |
|
|
|
|
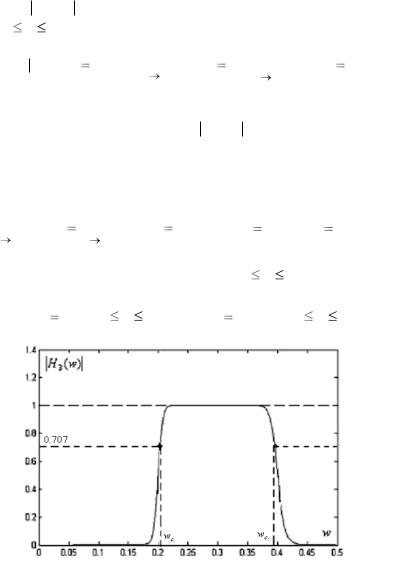
Полосовые пропускающие фильтры (bandpass-фильтры) реализуют функцию пропускания сигналов в заданной полосе частот. Возможный вариант функции АЧХ H3(w) для полосовых пропус-
кающих фильтров имеет вид, представленный на рис. 6.3.2а. Для указанных фильтров назначаются две частоты среза wc2 , wc2 , ко-
торые определяют нормированные частоты полосы пропускания. АЧХ полосовых фильтров удовлетворяет условиям
|
lim |
|
H3(w) |
|
0, |
H3 |
(wc ) |
|
H3 |
(wc ) |
0,707. |
|
lim |
H3(w) |
|
|
|||||||||
w 0 |
w 0,5 |
|
1 |
|
|
2 |
|
|||||
|
|
|
|
|
|
|||||||
Для идеальной АЧХ полосового пропускающего фильтра в области
частот, удовлетворяющих неравенству |
wс |
w |
wс , должно вы- |
|||||||
|
|
|
|
|
|
|
1 |
|
2 |
|
полняться условие |
|
|
|
|
|
|
|
|||
|
H3(w) |
|
1 для 0 w wc , |
|
H3(w) |
|
0 для |
wc |
w 0,5 . |
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
2 |
|
Рис. 6.3.2а. АЧХ для полосового пропускающего фильтра
194

Рис. 6.3.2б. АЧХ для полосового заграждающего фильтра
Полосовые заграждающие фильтры (stopbandpass-фильтры) задерживают сигналы в заданной полосе частот. Вариант АЧХ H4 (w) для полосовых задерживающих фильтров изображѐн на
рис. 6.3.2б. Так же как и для полосовых пропускающих фильтров, для указанных фильтров назначаются две частоты среза wс1, wс2 .
АЧХ полосовых заграждающих фильтров удовлетворяет условиям
|
lim |
|
H4 (w) |
|
1, |
H4 |
(wc ) |
|
H4 |
(wc ) |
0,707. |
|
lim |
H4 (w) |
|
|
|||||||||
w 0 |
w 0,5 |
|
1 |
|
|
2 |
|
|||||
|
|
|
|
|
|
|||||||
Приведѐнная классификация типов АЧХ не является полной. АЧХ, изображѐнные на рис.6.3.1а, 6.3.1б, 6.3.2а, 6.3.2б, являются базовыми. Целый ряд АЧХ для ЦФ может быть сформирован на основе рассмотренных базовых АЧХ.
6.3.2. Постановки задач синтеза ЦФ
Разберѐм некоторые варианты постановок задач синтеза ЦФ. В самом общем случае задача синтеза ЦФ интерпретируется как задача аппроксимации.
Пусть задаѐтся структура синтезируемого ЦФ – определены порядки числителя и знаменателя ПФ, что означает возможность формирования вектора с, состоящего из параметров фильтра. Задание структуры фильтра и набора параметров означает, что для любых значениях , T и вектора параметров с можно вычислить зна-
195

чения ПФ для синтезируемого ЦФ в виде модельной комплексной функции Hd (c, j T). Далее в задаче синтеза задаѐтся эталонная комплексная ПФ H0 ( j ), которая должна быть аппроксимирована с помощью модельной ПФ Hd (c, j T) синтезируемого ЦФ в заданной области частот, например для 0
состоит в подборе оптимального вектора параметров ЦФ c , который должен служить решением задачи аппроксимации эталонной комплексной функции H0 ( j ) с помощью модельной комплексной функции Hd (c, j T).
Во многих практических случаях возможны ситуации, когда
требуется |
решать задачу синтеза ЦФ, учитывая только АЧХ |
|||
|
H0 ( j ) |
|
, |
ФЧХ при этом не принимается во внимание. В более об- |
|
|
|||
щем случае синтезируются одновременно заданного вида АЧХ и ФЧХ. Иногда при синтезе учитываются дополнительные требования на передаточную функцию. Например, требование на вид ФЧХ – обеспечение линейности ( ) а ; требования к величи-
нам порядков k, m для числителя и знаменателя ПФ; требования, предъявляемые к параметрам c C0, для обеспечения
устойчивости; иногда при синтезе может возникать |
требование |
||||||||||
к |
крутизне АЧХ |
|
(Дб/Гц) в некотором заданном диапазоне частот |
||||||||
|
|
01 |
02 |
на |
основе |
обеспечения |
|
неравенства |
|||
|
|
|
|
|
|
|
|
|
|
||
|
dHd (c, j T) / d |
|
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
Рассмотрим более подробно синтез ЦФ как задачу аппроксима- |
|||||||||
ции. Пусть задан диапазон частот ( |
0, |
f ), на котором рассматри- |
|||||||||
вается построение ЦФ, определяется набор частот |
0, |
1,..., |
N 1, |
||||||||
|
|
f |
N 1, не обязательно распложенных равномерно, и в этих |
||||||||
частотных точках |
задаются значения |
эталонной |
ПФ H0 ( j |
i ), |
|||||||
i |
0, 1,..., N 1. |
|
|
|
|
|
|
|
|
||
Далее определяется модель ПФ Hd (c, j T), зависящая от век-
тора параметров c. Модель для ПФ может быть задана двумя способами: на основе соотношения (6.2.2), выведенного из разностных уравнений
196

k
ase j Ts
H |
d |
(c, j T ) |
|
s 0 |
|
, сT (a ,..., a , b ,..., b ), |
||
|
m |
|
||||||
|
|
|
0 |
k 1 |
m |
|||
|
|
|
1 |
b e j Tr |
|
|
||
|
|
|
|
|
r |
|
|
|
r1
ина основе соотношении (6.2.5), выведенного из представления ПФ на комплексной плоскости
|
|
|
|
|
|
k |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
(z |
s |
) |
|
|
|
(e j |
T |
s |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
H |
d |
(с, j Т ) |
H |
0 |
z(m k) |
s 1 |
|
|
H |
0 |
z(m k) |
s 1 |
|
|
|
, |
m |
|
|
m |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(z |
r |
) |
|
|
|
(e j |
T |
r |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
r 1 |
|
|
|
|
|
r 1 |
|
|
|
|
сT (H0, 1,..., k , 1,..., m) .
В первом и втором случаях вектор c модели Hd (c, j T) при фик-
сированных значениях порядков m, k имеет размерность m k |
1. |
||||
Требование устойчивости цифрового фильтра |
|
r |
1 |
|
, |
|
|
||||
r 1,..., m, удобно сформировать из второй модели. Это требование эквивалентно назначению ограничения на параметры c C0.
Затем формируются разности комплексных передаточных
функций H0 ( j i ), |
|
Hd (c, j |
iT) и функционал |
S(c, H0 ), |
опреде- |
||||
ляющий меру их близости |
|
|
|
|
|
|
|
||
Hd (c, j iT) |
H0 ( j |
i ) |
Hd (c, j |
iT), i |
0, 1,..., N |
1, |
|||
|
|
N 1 |
|
|
|
|
|
|
|
S(c, H |
0 |
) |
H* (c, j T) |
H |
d |
(c, j T). |
|
||
|
|
d |
i |
|
|
i |
|
||
|
|
i 0 |
|
|
|
|
|
|
|
Построение ЦФ сводится к решению задачи аппроксимации, решаемой на основе нелинейного программирования:
с arg{min S(c, H0 )}.
c C0
Отметим, что сформулированная в общем виде подобная задача синтеза ЦФ может быть решена для БИХ-фильтров только в исключительных случаях из-за того, что формируемая модель Hd (c, j T) зависит от вектора параметров c достаточно сложным
образом. Для КИХ-фильтров модельная Hd (c, j T) линейно зави-
сит от вектора c, аппроксимационная задача сводится к решению системы линейных уравнений.
197

Следует иметь в виду, что предложенная постановка является полезной для формирования правильного подхода к задачам синтеза ЦФ.
6.3.3. Метод билинейного z-преобразования
Решение задачи построения ЦФ может быть достаточно просто и эффективно осуществлено на основе метода билинейного z-преобразования с использованием аналоговых фильтров-прото- типов. Рассмотрим основные соотношения для реализации указанного метода.
Заметим, что ПФ для аналоговых фильтров, являющаяся комплексной функцией, определена в верхней полуоси комплексной
плоскости в точках p j а , ПФ для ЦФ определена на точках
единичной окружности в точках z e j dT , где |
a |
, |
d |
– частоты |
|
|
|
аналоговых и цифровых фильтров. Пусть реализуется перевод точек единичной окружности комплексной плоскости в точки верхней полуоси с помощью конформного отображения, называемого билинейным
p |
z |
1 |
, |
z |
p |
, |
(6.3.1) |
|
z |
1 |
p |
||||||
|
|
|
|
|
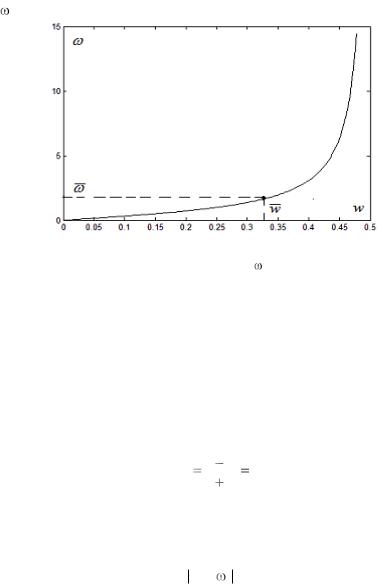
где 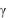 играет роль масштабирующего множителя. Найдѐм связь ана-
играет роль масштабирующего множителя. Найдѐм связь ана-
логовых |
а |
и цифровых |
d |
частот для указанного преобразования |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
j |
dT |
|
j |
dT |
|
j |
dT |
|
|
|
|
|
|
|
||
|
|
|
|
e |
2 |
|
e |
2 |
|
e |
2 |
|
|
|
|
|
|
|
|||
j a |
e j dT |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
, j a |
j |
tg |
d |
T |
. |
|
|
e j d |
1 |
|
j |
dT |
|
|
j dT |
|
|
j |
dT |
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
e |
2 |
|
e |
2 |
|
e |
2 |
|
|
|
|
|
|
|
|||
В дальнейшем будем полагать |
1. С учѐтом введѐнной нор- |
||||||||||||||||||||
мированной частоты |
w |
|
|
dT /2 |
запишем два варианта формул |
||||||||||||||||
для связи аналоговых и цифровых частот в результате билинейного преобразования переменных p и z:
a tg( dT /2), |
a tg( w) . |
(6.3.2) |
198 |
|
|
На рис. 6.3.3 изображѐн график нелинейной зависимости (6.3.2), связывающей аналоговые и цифровые нормированные частоты
и w.
Рис. 6.3.3. График нелинейной зависимости для аналоговых и цифровых частот и w
Исходя из предлагаемого перевода частот по формуле (6.3.2), вытекающей из билинейного z-преобразования (6.3.1), может быть предложен метод преобразования ПФ аналоговых фильтровпрототипов в ПФ для ЦФ. В заданной ПФ аналогового фильтрапрототипа, зависящей от оператора Лапласа p, сделаем формальную замену переменной p в ПФ аналогового фильтра с
помощью рассматриваемого билинейного преобразования. Получим ПФ цифрового фильтра Hd (c, z) , которая зависит от оператора z:
Hа |
c, p |
z |
1 |
Hd (c, z) . |
||
|
|
|
||||
z |
1 |
|||||
|
|
|
||||
Очевидно, что общий вид АЧХ ЦФ будет совпадать с АЧХ аналогового фильтра прототипа, изменится только масштаб по оси частот в соответствии с выведенными формулами (6.3.2) связи аналоговых и цифровых частот.
Рассмотрим пример АЧХ H( j ) аналогового фильтра второго порядка в виде колебательного звена H( p):
199
|
2k |
|
|
|
|
|
|
2k |
|
|||
H( p) |
0 |
0 |
|
, |
H( j ) |
|
|
|
0 |
0 |
. (6.3.3) |
|
p2 2 |
p |
2 |
( |
2 |
2 )2 |
(2 )2 |
||||||
|
|
|
|
|||||||||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
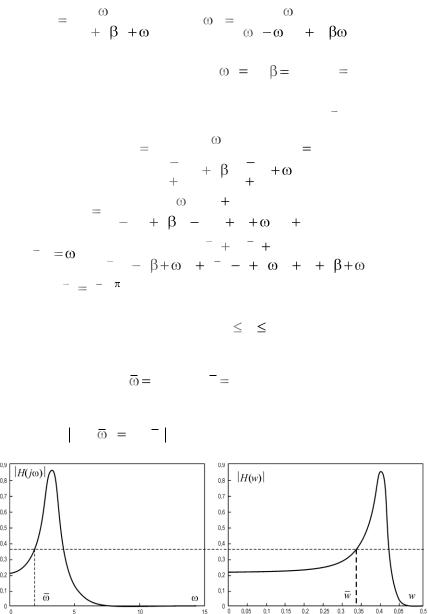
На рис. 6.3.4 изображена АЧХ для рассматриваемого аналогового фильтра для численных значений 0 5; 0,9; k0 2,6. Применим к ПФ H( p) (6.3.3) аналогового фильтра-прототипа билинейное преобразование, получим ПФ для ЦФ Н(z), H(z 1):
|
|
|
|
|
|
|
|
|
|
|
2k |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
H(z) |
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
2 |
|
z |
1 |
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
1 |
|
z |
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2k (z |
1)2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
(z 1)2 2 |
(z |
1)(z |
1) |
|
2 (z 1)2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
H(z 1) |
2k |
|
|
|
|
|
|
|
|
|
z 2 |
2z 1 |
1 |
|
|
|
|
. |
(6.3.4) |
|||
|
|
|
|
|
|
|
2 ) z 1( 2 2 |
2 ) (1 2 |
2 ) |
|||||||||||||
|
0 0 z 2 (1 2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
0 |
|
|
||
Так как z 1 |
|
e j2 w, то на основе (6.3.4) может быть вычислена |
||||||||||||||||||||
|
H(w) |
|
. На рис.6.3.4 изображѐн график |
|
H(w) |
|
|
|||||||||||||||
АЧХ для ЦФ |
|
|
|
в зави- |
||||||||||||||||||
симости от нормированных частот 0 |
w |
0,5. Процедура перевода |
||||||||||||||||||||
АЧХ аналогового фильтра-прототипа в АЧХ ЦФ с помощью билинейного преобразования иллюстрируется на рис. 6.3.4. Возьмѐм некоторые частоты 1,557 и w 0,331, которые связаны с помощью формулы (6.3.2) (см. рис. 6.3.3). Видно, что применѐнное билинейное преобразование меняет только масштаб кривых АЧХ, поскольку H( j )
 H(w) .
H(w) .
Рис. 6.3.4. Перевод АЧХ аналогового фильтра в АЧХ цифрового фильтра с помощью билинейного преобразования
200
