
getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie
.pdf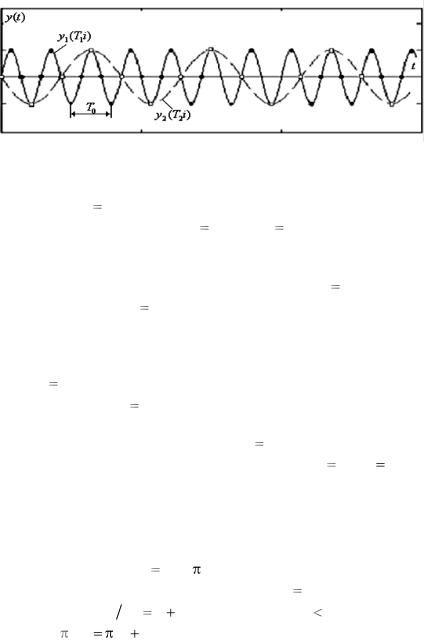
Рис. 3.4.1. Появление «кажущихся» частотных составляющих
Подвергнем исходный непрерывный сигнал y(t) дискретизации с частотой fd1 4 f0 – четыре точки дискретизации на один период T0 , интервал дискретизации T1 1/ 4 f0 , T1 T0 / 4. Дискретизованные значения исходного сигнала отмечены чѐрными жирными точками для синусоидального сигнала y1(T1i) (см. рис. 3.4.1). Уменьшим частоту дискретизации, примем еѐ равной fd 2 4 / 3 f0, период дискретизации Td 2 4 / 3T0, эти точки дискретизации на графике сигнала y2 (T2i) отмечены кругами на пунктирной линии. В пер-
вом случае частота дискретизации больше двойной частоты сигнала, дискретизованный сигнал воспринимается как сигнал с периодом Tk1 T0 и его «кажущаяся» частота совпадает с частотой ис-
ходного сигнала fk1 f0 . Во втором случае частота дискретизации меньше двойной частоты сигнала, дискретизованный сигнал вос-
принимается как сигнал с периодом Tk 2 3T0 |
и его кажущаяся час- |
тота меньше частоты исходного сигнала |
fk2 1/ Tk2 f0 / 3. |
Вследствие неудачного выбора частоты дискретизации имеет место очень сильное искажение информации, «кажущаяся» частота сигнала меньше частоты исходного сигнала, что и видно из рис. 3.4.1.
Рассмотрим более детально существо проблемы возникновения «кажущихся» частотных составляющих для дискретной синусои-
дальной функции y(i) |
sin(2 f0Ti). Введѐм |
частоту Найквиста, |
||||
равную половине частоты дискретизации, fN |
|
1/ 2T. Всегда мож- |
||||
но представить |
f0 fN |
p q, где p – целое, |
|
q |
|
1. Учитывая ра- |
|
|
|||||
венство 2 f0Ti |
( p q)i, запишем: |
|
|
|
|
|
|
|
101 |
|
|
|
|
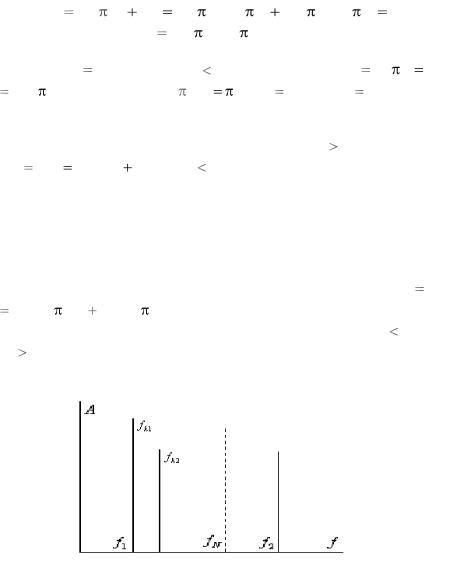
y(i) sin ( p q)i sin |
pi cos |
qi cos pi sin qi |
cos |
pi sin |
qi. |
Разберем первый пример – частота Найквиста больше частоты
сигнала – р 0, тогда f0 / fN |
1 и справедливо: |
y(i) |
sin qi |
sin 2 fk1Ti. Следует, что 2 fk1T |
q, fk1 fN q и |
fk1 |
f0 – «ка- |
жущаяся» частота совпадает с частотой исходного сигнала. Разберѐм второй пример – частота Найквиста меньше частоты сигнала –
в частном |
случае |
положим |
p четным, f0 / fN |
1, |
при этом |
fk2 fN q |
f0q / ( p |
q) и fk2 |
f0. Оказывается, |
что |
во втором |
примере «кажущаяся» частота меньше частоты исходного сигнала. Данные примеры позволяют сделать заключение, что для совпадения частоты сигнала и «кажущейся» частоты, частота Найквиста должна быть больше частоты дискретизуемого сигнала.
Вследствие неправильного выбора частоты дискретизации «кажущиеся» частоты приводят к эффекту маскировки (эффекту
наложения |
частот). Рассмотрим двухчастотный |
сигнал |
y(i) |
||||
A sin 2 |
f Ti A sin 2 f Ti. Допустим, что выбрана частота дис- |
||||||
1 |
1 |
2 |
2 |
|
|
|
|
кретизации |
таким |
образом, что |
выполнились условия |
f1 |
fN , |
||
f2 fN . |
Расположение частот |
f1, f2 и частоты |
Найквиста |
fN |
|||
проиллюстрировано на амплитудном спектре, изображѐнном на рис. 3.4.2.
Рис. 3.4.2. Амлитудный спектр двухчастотного сигнала и эффект маскировки
При такой частоте дискретизации, которая определяется положением частоты f N , первая синусоида воспринимается с «кажу-
102

щейся» частотой fk1 |
f1 , вторая синусоида |
воспринимается с |
«кажущейся» частотой |
f k2 f 2. В данном |
дискретизованном |
двухчастотном сигнале появляется ложный сигнал с низкой частотой – смещѐнный в низкочастотную область, который во многих случаях может «маскировать» исходный сигнал, так как fk 2 f1 .
Дискретизация с такими параметрами может катастрофически исказить исходный сигнал – спектр высокочастотного сигнала перемещается в низкочастотную область, и наложиться на спектр основного сигнала.
3.4.3. Теорема Котельникова
Установим возможность точного восстановления непрерывных сигналов по их дискретным значениям. В рамках теоремы Ко-
тельникова рассматриваются сигналы, принадлежащие к классу сигналов с финитным преобразованием Фурье. Сигнал y(t) имеет
финитное преобразование Фурье, обозначаемое как Сf ( j ), если: |
|||||||
1) Сf ( j ) 0 для всех частот |
|
|
|
|
; 2) С f ( j ) тождественно не |
||
|
|
||||||
равно нулю для частот |
|
, где |
– верхнее значение частоты |
||||
|
|||||||
сигнала – полоса сигнала. Теорема Котельникова утверждает, что для сигналов с финитным преобразованием Фурье возможно точное восстановление сигнала по дискретным наблюдениям, если
круговая частота дискретизации |
d удовлетворяет строгому нера- |
|
венству d 2 , где |
2 f p , |
f p – полоса сигнала, Гц, fd 2 f p. |
Представим исходный сигнал y(t) на основе обратного преобра-
зования Фурье, если С f ( j |
) – финитное преобразование Фурье: |
||||||||||||||||||||
|
|
|
|
|
|
y(t) |
C |
f |
( j )e j t d . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возьмѐм |
, разложим функцию С f ( j |
) |
в комплексный ряд |
||||||||||||||||||
Фурье на данном интервале ( |
|
, ): |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
j |
2 |
l |
|
|
|
1 |
|
|
|
|
j |
2 |
l |
|
|
С |
|
( j ) |
c |
|
e |
|
, c |
|
|
C |
|
( j |
)e |
|
d . (3.4.2) |
||||||
f |
fl |
2 |
|
fl |
|
|
|
f |
|
2 |
|
||||||||||
|
|
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |
|
|
|
|
|
|
|
|
||
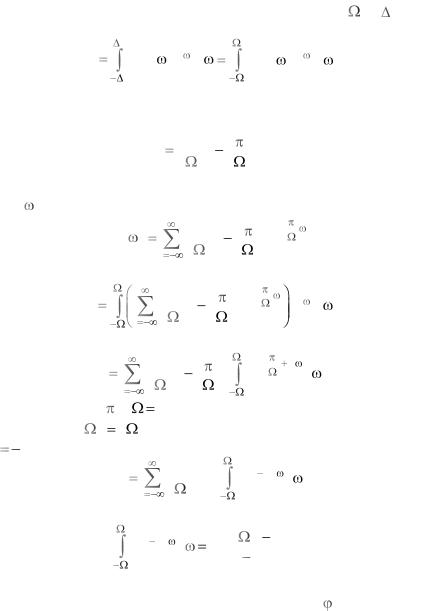
Учитывая введѐнное соотношение между величинами |
и , за- |
||||||
пишем |
|
|
|
|
|
|
|
y(t) |
C |
f |
( j )e j t d |
C |
f |
( j )e j t d . |
(3.4.3) |
|
|
|
|
|
|
||
Справедливо равенство, вытекающее из (3.4.2), (3.4.3), связывающее дискретные значения сигнала и коэффициенты фурьеразложения
cfl |
1 |
y |
2 |
l . |
|
2 |
2 |
||||
|
|
|
Подставим коэффициенты фурье-разложения c f l
С f ( j ) из (3.4.2):
|
|
|
|
1 |
|
2 |
l e j |
2 |
l |
С |
f |
( j ) |
|
y |
2 |
||||
|
2 |
2 |
|
||||||
|
|
|
|
|
|
|
|||
|
|
|
l |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
в выражение для
. (3.4.4)
Подставим выражение (3.4.4) в ( 3.4.3)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
y(t) |
|
|
|
1 |
y |
|
2 |
l e j |
|
|
l |
|
e j t d . |
|
||||||||
|
|
|
2 |
|
|
|
||||||||||||||||
l |
|
2 |
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переменим порядок интегрирования и суммирования |
|
|||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
e j |
2 |
|
l t |
|
|
||||
|
y(t) |
|
|
|
y |
|
l |
|
2 |
|
d . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
l |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сделаем замену 2 |
/ 2 |
|
T, при этом частота дискретизации ока- |
|||||||||||||||||||
жется равной |
d |
2 , |
|
и переобозначим индексы суммирования |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l i : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t) |
|
|
|
|
1 |
y(Ti) |
e j(t |
Ti) |
d |
. |
(3.4.5) |
||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
i |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интеграл в (3.4.5) легко вычислить |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
e j(t |
Ti) d |
|
|
2sin |
(t |
|
Ti) |
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t |
Ti) |
|
|
|
|
|||
В результате сигнал y(t) на основании (3.4.5) может быть представлен в виде разложения по базисным функциям i (t, T) с весовыми коэффициентами y(Ti) :
104

y(t) |
y(Ti) i (t, T), i (t,T) |
sin (t |
Ti) |
. |
(t |
|
|||
|
i |
Ti) |
||
|
|
|
|
|
Таким образом, в соответствии с теоремой Котельникова сигнал с финитным преобразованием Фурье с полосой при выборе час-
тоты дискретизации d 2 допускает точное восстановле-
ние – выполнение равенства (3.4.1).
Теорема Котельникова имеет чрезвычайно большое значение для практики задач ЦОС.
3.4.4. Противомаскировочные фильтры
Устранение эффекта маскировки (наложения) может быть реализовано двумя способами.
Во-первых, устранение может быть осуществлено с помощью назначения высокой частоты дискретизации, которую необходимо выбрать таким образом, чтобы еѐ величина была бы более чем в два раза больше, чем значение полосы сигнала.
Во-вторых, если по некоторым техническим причинам нельзя назначить высокую частоту дискретизации, то исходный непрерывный сигнал, прежде чем подвергнуть дискретизации, следует пропустить через аналоговый низкочастотный фильтр с частотой среза с 2 fс и с АЧХ, изображенной на рис. 1.3.6. В отфиль-
трованном сигнале не должны содержаться составляющие с частотой выше, чем указанная частота среза c. Низкочастотный фильтр
должен отсечь неинформативные (помеховые) высокочастотные составляющие сигнала. Для частоты дискретизации подобным образом отфильтрованного сигнала необходимо выполнение неравенства fd 2 fc.
Указанная фильтрация называется противомаскировочной, а используемые аналоговые фильтры – противомаскировочными.
Список вопросов для самопроверки к гл. 3
1.Какое определение для функций законов распределения для случайных сигналов приведено в разд. 3.1?
2.Какое определение для функций плотностей вероятностей для случайных сигналов приведено в разд. 3.1?
105
3.Какое определение для моментных характеристик случайных сигналов приведено в разд. 3.1?
4.В чѐм состоит алгоритм вычисления оценок плотностей вероятностей и моментных характеристик на множестве реализаций случайных сигналов?
5.Какие варианты определений для стационарных случайных сигналов используются в задачах ЦОС?
6.Какое определение для эргодических случайных сигналов используется в задачах ЦОС?
7.В чѐм состоит алгоритм вычисления оценок моментных характеристик для стационарных эргодических случайных сигналов в дискретном случае?
8.Какие определения для нестационарных случайных сигналов используются в задачах ЦОС?
9.Какие определения для локальных интервалов используются в задачах ЦОС?
10.В чѐм состоит алгоритм вычисления локальных оценок статистических характеристик нестационарных случайных сигналов?
11.В чѐм состоят причины возникновения аддитивных и мультипликативных трендов в сигналах?
12.В чѐм состоит методика устранения трендов для нестационарных случайных сигналов?
13.В чѐм состоят причины возникновения аномальных значений
внаблюдениях случайных сигналов?
14.В чѐм состоит методика устранения аномальных значений в наблюдениях сигналов?
15.Какие варианты и характеристики процедур дискретизации непрерывных сигналов приведены в разд. 3.4?
16.В чѐм состоит формулировка и описание основных этапов вывода теоремы Котельникова?
17.В чѐм состоят причины возникновения «кажущихся частот»
вдискретизованных сигналах?
18.В чѐм состоит методика устранения «кажущихся частот» в дискретизованных сигналах?
106

Глава 4. ЭЛЕМЕНТЫ СПЕКТРАЛЬНОГО АНАЛИЗА ДИСКРЕТНЫХ СИГНАЛОВ
4.1.Дискретное преобразование Фурье
4.1.1.Оценивание параметров полигармонических моделей и задачи спектрального анализа
Пусть y(i) y(Ti) – наблюдения действительного дискретизо-
ванного сигнала, представляющего собой сумму гармонических (узкополосных) составляющих, i 0, 1,..., N 1, N – число наблюдений, T – интервал дискретизации. Рассмотрим для подобного сигнала на ограниченном временном интервале модельную полигармоническую функцию вида
|
|
L |
|
|
|
|
|
yM (c, Ti) |
(al cos |
lTi bl sin lTi), |
i |
0, 1,..., N |
1. |
(4.1.1) |
|
|
l |
1 |
|
|
|
|
|
Вектор |
параметров для |
этой модели |
сТ |
(a ,..., a , b ,..., b , |
|||
|
|
|
|
|
1 |
L 1 |
L |
1,..., |
L ) имеет размерность 3L. Будем полагать, что имеет место |
||||||
случай, когда L – число составляющих в сигнале – известно из априорных сведений.
Для решения задачи оценивания параметров модели (4.1.1) необходимо сформировать функционал S(c, y) , являющийся мерой
близости наблюдений и модели, который записывается известным образом:
N 1 |
|
L |
2 |
|
|
|
|
||
S(c, y) |
y(i) |
al cos lTi bl sin lTi |
. |
(4.1.2) |
i 0 |
l |
1 |
|
|
Оценивание оптимального вектора параметров полигармонической модели с сводится к решению задачи минимизации сформированного функционала
с |
arg{min S(c, y)}, |
с T (a ,..., a , b ,..., |
b , |
1 |
,..., |
L |
). |
|
|
c |
1 |
L 1 |
L |
|
|
||
|
|
|
|
|
|
|
|
|
Нахождение оптимального вектора параметров с |
осуществляет- |
|||||||
ся на основе решения достаточно сложной задачи поиска минимума функционала S(c, y). Проблемы определения минимума функцио-
нала (4.1.2) обусловлены спецификой модели (4.1.1), представляю-
107

щей собой сумму синусоидальных функций, нелинейно зависящих от частотных параметров L . В силу указанных особенностей модели функционал S(c, y) является многоэкстремальным.
Применим технологическое упрощение в задаче минимизации рассматриваемого функционала, заключающееся в разделении параметров, входящих в модель (4.1.1) линейно и нелинейно. Нелинейные параметры фиксируются и находятся частично оптимальные линейные параметры с помощью решения соответствующей системы линейных уравнений. Вычисляется значение частично оптимального функционала при фиксированных нелинейных параметрах и частично оптимальных линейных параметрах. Далее производится поиск минимума частично оптимального функционала по нелинейным параметрам, позволяющий получить окончательное решение.
Поясним методику реализации предлагаемого технологического
упрощения. Положим, что |
Т |
( |
1,..., 2L ) (a1,..., aL , b1,..., bL ) - |
||
|
|||||
вектор размерности (2L, 1), состоящий из параметров, входящих в |
|||||
модель линейно; |
T |
( 1,..., |
|
L) |
– вектор размерности (L, 1), со- |
|
|
||||
стоящий из нелинейных параметров. Введѐм векторную базисную функцию ( , Ti) размерности (2L, 1), состоящую из синусои-
дальных функций
T ( , Ti) (cos 1Ti,..., cos LTi, sin 1,..., sin LTi).
Модель полигармонического сигнала в таком случае можно будет записать в виде скалярного произведения
|
y ( , |
, Ti) |
T |
( , Ti). |
|
|
|
M |
|
|
|
|
|
Оптимизируемый |
функционал |
S( |
, |
, y) оказывается |
квадра- |
|
тичной формой от линейных параметров |
: |
|
||||
|
|
N 1 |
|
T |
( , Ti))2. |
|
S( , |
, y) |
(y(i) |
(4.1.3) |
|||
|
|
i 0 |
|
|
|
|
Фиксируем частотные параметры |
|
сonst для функционала (4.1.3) |
||||
и на первом этапе оптимизации находим частично оптимальные линейные параметры ( ) из решения системы линейных уравнений
( ) arg{ min S( , , y}.
,const
Записываем выражение для вычисления значений частично оптимального функционала
108
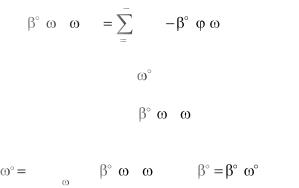
|
N 1 |
T ( , Ti))2 |
S( ( ), , y) |
(y(i) |
i0
ина втором этапе оптимизации на его основе находим оптимальные
нелинейные частотные параметры путѐм подпоиска по частотным параметрам для частично оптимального функционала. Необхо-
димо отметить, что функционал S( ( ), , y) является многоэкс-
тремальным. Оптимальные линейные параметры являются функциями оптимальных частотных параметров
arg{min S( ( ), , y)}, ( ).
Описанное технологическое упрощение, очевидно, эффективно лишь при малой размерности вектора нелинейных параметров.
Вычислительные трудности оптимизации сформированного функционала происходят от того, что для достижения достаточно высокой точности подгонки модели к наблюдениям осуществляется подпоиск многоэкстремального функционала по частотным нелинейным параметрам. Проблемы решения задачи оценивания параметров полигармонической модели многократно увеличиваются, если оказывается неизвестным число гармонических (узкополосных) составляющих в наблюдениях сигнала.
Оценивание параметров полигармонических моделей применяется для решения одного из вариантов задачи спектрального анализа – определения оценок амплитуд и частот составляющих в наблюдениях.
4.1.2. Дискретное преобразование Фурье для действительных сигналов
Один из возможных путей, радикально упрощающий задачу оценивания параметров для полигармонических моделей, состоит в подмене исходной задачи на видоизменѐнную задачу с линейной моделью, в которой используются синусоидальные базисные функции с фиксированными частотами. Частоты базисных функций располагаются равномерно на частотной оси с достаточно мелким шагом; как правило, число синусоидальных базисных функций в модели должно быть много больше числа частотных составляющих в наблюдениях.
109

Перейдѐм к рассмотрению дискретного преобразования Фурье (ДПФ) для действительных сигналов. Так же как и в разд. 4.1.1, y(i) y(Ti) являются наблюдениями действительного дискретизо-
ванного сигнала, i 0, 1,..., N 1, N – число наблюдений, T – интервал дискретизации. В самом общем случае для ДПФ не выдвигается никаких специальных требований к наблюдениям сигнала.
Полигармоническую модель с фиксированными частотами для ДПФ в действительном случае примем в следующем виде:
|
|
|
|
|
a0 |
N 1 |
|
|
|
|
|
|
|
|
||
|
yM (c, Ti) |
|
|
(ak cos |
kTi |
bk sin |
|
kTi). |
(4.1.4) |
|||||||
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Указанные частоты |
k |
для модели (4.1.4) подчиняются соотноше- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ниям: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
k, |
k |
|
1, 2,..., N 1, |
|
2 |
|
, |
|
|
k. |
||||
k |
|
|
|
|
|
|
|
|
k |
|||||||
|
NT |
|
|
|
|
|
|
|
|
NT |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вектор параметров |
модели |
cT (a , |
a ,..., |
a |
, b ,..., b |
) имеет |
||||||||||
|
|
|
|
|
|
|
|
0 |
1 |
|
N 1 |
1 |
N 1 |
|
||
размерность (2N 1, 1). |
|
Оптимизируемый |
|
квадратичный |
по с |
|||||||||||
функционал S(c, y) записывается по аналогии с (4.1.2):
|
|
|
N 1 |
|
|
|
|
a0 |
|
N 1 |
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
S(c, y) |
y(i) |
|
|
|
|
ak cos kTi |
bk sin |
kTi |
. |
(4.1.5) |
|||||||||||
|
|
2 |
|
|
|||||||||||||||||
|
|
|
i 0 |
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Оценки параметров c |
|
для модели (4.1.4) находятся из решения за- |
|||||||||||||||||||
дачи минимизации функционала |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
с |
|
|
arg{min S(c, y)}. |
|
|
|
|
|
(4.1.6) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
Для |
модели (4.1.4) |
|
введѐм векторную |
базисную |
функцию |
||||||||||||||||
( , Ti) размерности (2N |
|
1, 1): |
|
|
|
|
|
|
|
|
|
||||||||||
|
Т ( |
, Ti) |
( |
1 |
( |
, |
Ti), |
2 |
( , Ti),..., |
2N 1 |
( |
, Ti)) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 , |
cos |
2 |
1Ti,..., |
|
cos |
2 |
|
(N |
1)Ti, sin |
2 |
|
1Ti,..., sin |
2 |
(N |
1)Ti . |
||||||
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
NT |
|
|
|
|
|
|
NT |
|
|
|
NT |
|
|
|
NT |
|
|
||
Обратим внимание на то, что благодаря выбранным частотам данная векторная базисная функция не зависит от интервала дискретизации T:
T ( , i) |
1 |
, cos |
2 |
1i,..., cos |
2 |
|
(N |
1)i, sin |
2 |
1i,..., sin |
2 |
(N 1)i . |
|
2 |
N |
N |
N |
N |
|||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
110 |
|
|
|
|
|
||
