
getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie
.pdf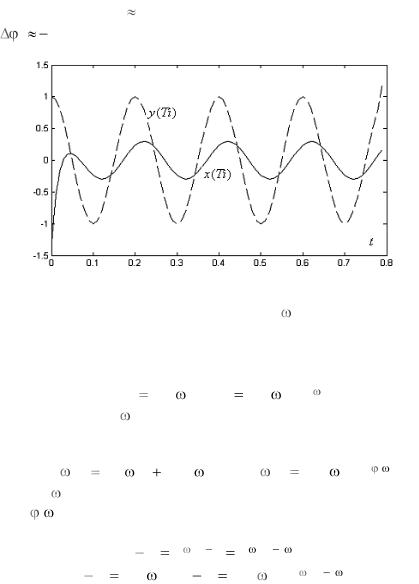
сделать приближѐнные оценки для искажѐнной амплитуды, которая равняется А0 0,25 и фазового запаздывания, равного
0 |
0,55. |
|
Рис. 6.2.1. Моделирование установившегося режима для ЦФ
Введѐм комплексный коэффициент H( j T), не зависящий от дискретного индекса i и позволяющий связать входной y(Ti) и вы-
ходной x(Ti) |
комплексные синусоидальные сигналы в устано- |
вившемся режиме: |
|
|
x(Ti) H( j T)y(Ti) H( j T) ej Ti. |
Коэффициент |
H( j T) по определению является передаточной |
функцией. Отметим, что ПФ является комплексной функцией частоты и может быть представлено в показательной форме
|
|
H( j T) |
H ( T) |
jH |
2 |
( T), |
H( j T) |
|
H( j T) |
|
e j ( T) , |
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
где |
|
H( j T) |
|
– амплитудно-частотная характеристика (АЧХ) для |
||||||||
|
|
|||||||||||
ЦФ; |
|
( T) – его фазочастотная характеристика (ФЧХ). |
||||||||||
Произведѐм вычисления для сдвинутых комплексных синусоид |
||||||||||||
|
|
|
|
y(i s) e j T(i s) |
e j Tie j Ts , |
|||||||
x(i r) H( j T)y(i r) H( j T) e j Tie j Tr .
Подставив эти выражения в разностное уравнение для ЦФ, получим формулу для передаточной функции ЦФ
181

|
m |
|
|
|
|
|
|
k |
|
H( j T)e j Ti |
b |
H( j T) e j Tie |
j Tr |
a |
e j Tie j Ts , |
||||
|
r |
|
|
|
|
|
|
s |
|
|
r 1 |
|
|
|
|
|
s |
0 |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
a e j |
Ts |
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
H( j |
T ) |
|
s |
0 |
|
. |
|
(6.2.2) |
|
|
|
m |
|
|
||||
|
|
|
|
|
j Tr |
|
|
||
|
|
|
1 |
b e |
|
|
|||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
r 1 |
|
|
|
|
АЧХ и ФЧХ, которые вычисляются на основе ПФ (6.2.2), позволяют определить амплитудные и фазовые искажения для выходного синусоидального сигнала.
Любому разностному уравнению ЦФ вида (6.1.1) может быть поставлена в соответствие передаточная функция вида (6.2.2). К примеру, для разностного уравнения
x(i) 2x(i 1) 3x(i 2) 4x(i 3) 5y(i) 6y(i 1)
передаточная функция для фиксированного значения интервала дискретизации T будет иметь вид
|
5 |
6e j T |
|
H( j T) |
|
|
. |
1 2e j T |
3e j 2T 4e j 3T |
||
Приведѐм выражения передаточных функций для ЦФ первого и второго порядка вида (6.1.3), (6.1.4)
H( j T) |
a0 |
, H( j T) |
a0 |
|
. (6.2.3) |
1 b e j T |
1 b e j T |
b e j 2T |
|||
|
1 |
|
1 |
2 |
|
Очевидно, ПФ является периодической функцией частоты с периодом 2 T . В самом деле
|
j |
2 |
Ts |
|
|
|
|
|
|
|
|
|
2 |
|
e |
T |
e |
j Ts |
e |
j2 s |
e |
j |
Ts |
, |
H( j T) H j |
T . |
|||
|
|
|
|
|
|
|
T |
Для действительных параметров ЦФ a0, a1,...,ak , , b1,..., bm
АЧХ |
симметрична |
|
относительно |
|
частоты |
Найквиста |
|||
N |
2 fN 2 / 2T. Представим ПФ в виде суммы косинусных и |
||||||||
синусных членов, положим b0 1 |
|
|
|
|
|
|
|||
|
|
|
k |
|
|
|
k |
|
|
|
|
|
as cos |
Ts |
j |
|
as sin |
Ts |
|
|
H( j T) |
s |
0 |
|
|
s |
0 |
|
. |
|
|
m |
|
|
m |
|
|||
|
|
|
|
|
|
|
|||
|
|
|
br cos |
Tr |
j |
|
br sin |
Tr |
|
|
|
r |
0 |
|
|
r |
0 |
|
|
|
|
|
182 |
|
|
|
|
|
|

Рассмотрим |
частоты, |
симметричные |
относительно |
N , |
|||
1 |
Т |
, |
2 |
Т |
. Заметим, что |
|
|
|
|
|
|
||||
|
|
|
cos |
1Ts |
cos 2Ts, sin 1Ts |
sin 2Ts. |
|
Введѐм функции частоты A( ), B( ) для действительной и мни- |
|||||||
мой части числителя ПФ, ( ), ( ) – для действительной и мни-
мой части знаменателя ПФ. С учѐтом того, что все параметры являются действительными, получим следующие соотношения
H( j T) |
A( 1) |
jB( 1) |
, H( j T) |
A( 2 ) |
jB( 2 ) |
, |
1 |
( 1) |
j ( 1) |
2 |
( 2 ) |
j ( 2 ) |
|
|
|
|||||
H( j 1T) H*( j 2T).
Из последнего равенства вытекает свойство симметрии АЧХ (ФЧХ)
H( j 1T)
 H( j 2T) , ( 1) ( 2 ).
H( j 2T) , ( 1) ( 2 ).
Как следует из свойств периодичности, ПФ имеет смысл рассматривать для частотного диапазона, удовлетворяющего неравенству 0 Т 2 . Иногда целесообразно введение нормированной частоты w T/2 , и определение ПФ H(w) в виде функции вве-
дѐнной нормированной частоты с учѐтом ограничения 0 w 1. Для действительных параметров ПФ можно ограничиться диапазоном 0 w 0,5. В том случае, если значения АЧХ изменяются в широких пределах, удобно для графических рассмотрений применять логарифмический масштаб LH(w) 20log10 H(w) . Измене-
ние АЧХ H(w) в десять раз соответствует изменениям АЧХ в ло-
гарифмическом масштабе на 20 Дб. Пользуясь таким масштабом, на одном графике можно изобразить значения АЧХ для большого динамического диапазона по амплитуде.
|
|
|
|
T) |
|
и ФЧХ ( Т) для цифрового аперио- |
||||||||||||
Вычислим АЧХ |
H( j |
|
||||||||||||||||
дического звена, сделав необходимые преобразования в (6.2.3): |
||||||||||||||||||
H( j T) |
|
|
|
a0 |
|
|
|
|
|
|
a0 |
|
|
|
|
|||
1 |
b e j |
|
T |
1 |
b cos |
T |
jb sin T |
|
|
|||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
a0 (1 |
b1 cos |
T) |
ja0b1 sin |
T |
|
|
|||||||||
|
|
|
|
|
|
|
|
, |
|
|
||||||||
|
|
|
|
(1 b cos T)2 |
(b cos |
T)2 |
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
H1( T) |
a0 (1 |
b1 cos |
|
T) |
, H2 ( T) |
|
|
a0b1 sin |
T |
, |
||||||||
1 2b cos |
T |
|
b2 |
1 |
2b cos |
T b2 |
||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
183 |
|
|
|
|
|
|
|
|
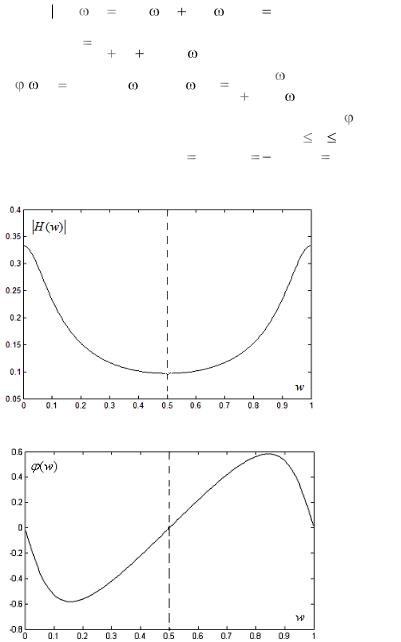
H( j T |
|
(H2 |
( T) |
H2 |
( T))1/2 |
|
|||||
|
|
1 |
|
2 |
|
|
|
a0 |
|
, |
|
|
|
(6.2.4) |
|
2 |
2b cos |
1/2 |
|
|
|
||||
|
(1 b |
T) |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
( Т) arctg(H2 ( |
T) / H1( |
T)) |
|
|
b1 sin |
T |
. |
||
1 |
|
b1 cos |
T |
||||||
|
|
|
|
|
|
||||
На рис. 6.2.2 представлено изображение АЧХ |
|
H(w) |
и ФЧХ (w) |
||||||
из (6.2.4) для нормированной частоты w в диапазоне 0 |
w 1. Па- |
||||||||
раметры ЦФ принимали значения a0 |
0,15; b1 |
0,55, |
T 0,01 c. |
||||||
Действительный полюс данного ЦФ располагается на правой полуоси.
Рис. 6.2.2а. АЧХ для цифрового апериодического звена
Рис. 6.2.2б. ФЧХ для цифрового апериодического звена
184

Видно, что АЧХ симметрична и ФЧХ антисимметрична относи-
тельно w |
0,5. Оценка амплитудного искажения может быть оце- |
|||||||
нена |
на основе рис. 6.2.2а; |
для |
f |
5 Гц и частоте |
Найквиста |
|||
fN |
1/ 2T |
50 Гц |
вычислим |
|
нормированную |
частоту |
||
w |
f / fN |
0,1 и |
H(0,1) |
0,25. |
Оценка фазового запаздывания |
|||
определяется из рис. 6.2.2б – |
(0,1) |
0,55. |
|
|||||
Многие практические задачи, связанные с анализом и построением ЦФ, решаются с помощью представлений ПФ на комплексной плоскости. Вводится переменная с обозначением z 1
z e j T , которая представляет собой при фиксированной частоте некоторую точку единичной окружности на комплексной плоскости. Тогда запишем ПФ как функцию отношения полиномов от введѐнных переменных 
k
as z s
H(z 1) |
s 0 |
m |
1 |
b z r |
|
r |
r |
1 |
H(z) H0zm k H0
, H(z)
(z), H0
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
(z |
s ) |
||
H |
0 |
z(m k) |
s 1 |
|
, |
|||
m |
|
|||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
(z |
r ) |
||
|
|
|
|
r |
1 |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
(z |
s ) |
|
|
||
(z) |
|
s |
1 |
|
|
, |
(6.2.5) |
|
|
m |
|
||||||
|
|
|
|
|
|
|||
|
|
|
(z |
r ) |
|
|
||
|
|
r |
1 |
|
|
|
|
|
где |
комплексные числа |
s , |
s 1,.., k, являются нулями; r , |
r |
1,..., m, – полюсами ПФ; |
H0 |
может трактоваться как комплекс- |
ный коэффициент усиления.
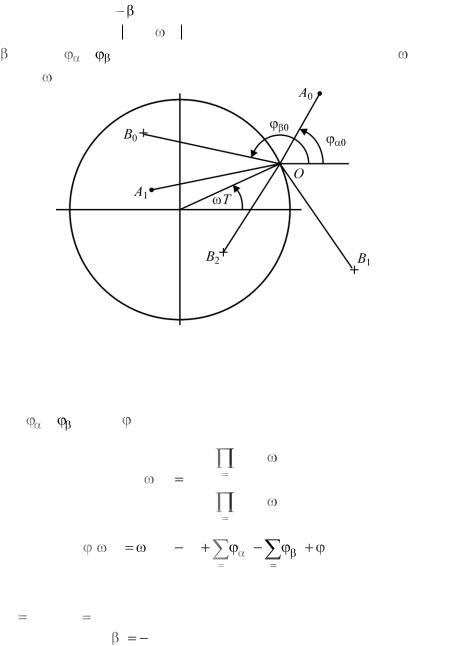
Крайне полезно для задач ЦОС рассмотреть геометрическую интерпретацию ПФ. На рис. 6.2.3 изображена единичная окружность на комплексной плоскости. Угол Т задаѐт положение переменной z на единичной окружности – точку O, стрелкой обозначено направление положительного вращения. Точки с кружками соответствуют обозначению нулей ПФ (А0, А1,...), звѐздочки обо-
значают положение полюсов (В0 , В2,...). Модули z s числителя ПФ H(z) определяются длинами векторов OAs ( T) , соединяющих точку O с нулями s. Аналогичным образом вводятся мо-
185
|
|
|
|
дули векторов |
z |
r |
знаменателя ПФ, которые определяются |
длинами векторов OBr ( T) , соединяющих точку O с полюсами к . Углы s , r определяют угловой наклон векторов OAs ( T)
и OBr ( T).
Рис.6.2.3. Геометрическая интерпретация ПФ на комплексной плоскости
Модуль ПФ АЧХ представится как отношение произведений длин указанных векторов. ФЧХ для ЦФ, исходя из геометрической картины рис. 6.2.3, определится соответствующей угловой суммой
для s , r , угол |
0 задаѐтся параметром H0: |
|
|||||||||
|
|
|
|
|
k |
|
|
|
|
||
|
|
|
|
|
|
|
OAs ( T) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
H( j T) |
|
H0 |
s |
1 |
|
|
|
, |
|
|
|
|
|
|
|
|||||||
|
|
m |
|
|
|||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
OBr ( T) |
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
r |
1 |
|
|
|
|
|
|
|
|
|
|
k |
|
|
m |
|
||
( Т) |
T(m |
k) |
|
s |
|
|
r 0 . |
(6.2.6) |
|||
|
|
|
|
s |
1 |
|
r 1 |
|
|||
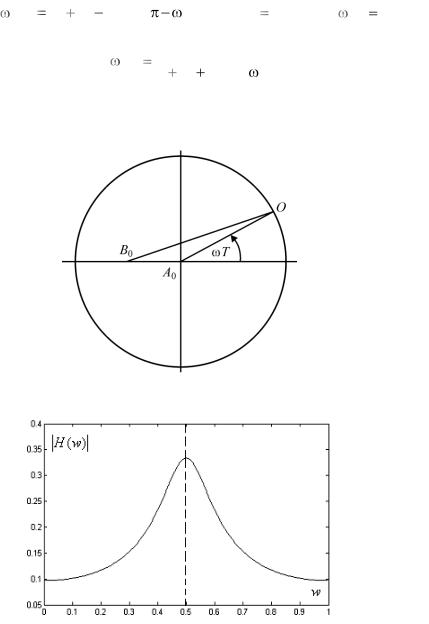
Рассмотрим пример построения АЧХ с использованием (6.2.6) для ЦФ в виде апериодического звена (6.1.3) с параметрами
а0 0,15, b1 0,55, с расположением действительного полюса на
левой полуоси, |
1 |
0,55 (рис. 6.2.4а). Нетрудно видеть, что |
|
|
|
|
|
186 |
|
ОВ ( Т) |
|
(1 b2 |
2b cos( |
|
T))1/2, |
H |
a , |
|
ОA ( Т) |
|
1. |
|||||
|
|
|
|
|
|||||||||||||
|
0 |
|
1 |
1 |
|
|
|
|
|
0 |
0 |
|
|
0 |
|
|
|
Легко записать формулу для ПФ |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
H( j T) |
|
|
|
|
a0 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
(1 |
b |
2 |
2b cos |
1/2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
T) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
На рис. 6.2.4б представлена рассматриваемая АЧХ. Отметим существенную особенность данной АЧХ из-за расположения полюса – при возрастании частоты АЧХ возрастает.
Рис. 6.2.4а. Геометрическая интерпретация ПФ для апериодического звена на комплексной плоскости
Рис. 6.2.4б. АЧХ для цифрового апериодического звена с действительным полюсом на левой полуоси
187

Учитывая возможность рассмотрения ПФ на комплексной плоскости с введѐнной переменной z, найдѐм связь между ПФ, как функции z, и импульсно-переходной функцией.
Запишем реакцию линейного фильтра с помощью импульснопереходной функции, для простоты рассмотрения примем начальные условия нулевыми
i
x(i) |
h(i s)y(s), i 0, 1,..., . |
s 0
На основании материалов разд. 2.6 можно сразу записать z-пре- образования для выходной последовательности на основе произведения z-преобразований входной и весовой последовательностей
X(z) H(z)Y(z).
Ясно, каким образом связывается импульсно-переходная функция и передаточная функция: ПФ на комплексной плоскости для принятой переменной z является z-преобразованием для импульснопереходной функции.
6.2.2. Устойчивость ЦФ
Устойчивость ЦФ является исключительно важной характеристикой, которую необходимо принимать во внимание в задачах синтеза ПФ. Разберѐм определение устойчивости для ЦФ. Один из вариантов определения состоит в том, что ЦФ является устойчи-
вым, если для любого ограниченного входного сигнала, поступающего на фильтр, выходной сигнал также является ограниченным.
Это означает, что для входной последовательности с ограничением Y , для которого выполняется неравенство y(i) Y при любых i, ЦФ является устойчивым, если для выходной последовательности существует значение ограничения X , которое обеспечивает для любых i неравенство x(i) X.
Очевидно, что КИХ-фильтры всегда являются устойчивыми с точки зрения сделанного определения. Действительно, из разностного уравнения КИХ-фильтра при ограниченном входном сигнале и конечном числе ограниченных коэффициентов фильтра
|
k |
x(i) |
s y(i s) |
s0
188

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при |
|
y(i) |
|
|
Y i |
0, 1,..., |
и |
|
as |
|
A, s 0, 1,..., k, |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
следует, что выходной сигнал также ограничен |
|||||||||||||||||||||||||||||||
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x(i) |
|
|
|
as |
|
y(i s) |
A |
y(i) |
|
A(k 1)Y , X A(k 1)Y. |
||||||||||||||||||||
|
|
s |
0 |
|
|
|
|
|
|
|
|
|
s 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При синтезе ПФ для БИХ-фильтров следует иметь в виду, что одна и та же структура БИХ-фильтра при одних значениях параметров может быть устойчивой, при других значениях – неустойчивой. Приведѐм здесь достаточные условия устойчивости БИХфильтров. Разберѐм простой пример, позволяющий прояснить существо подхода.
Пусть рассматривается БИХ-фильтр первого порядка с параметрами b1, a0, которые в общем случае являются комплексными. За-
пишем разностное уравнение и выражение для передаточной функции:
x(n) b x(n 1) a y(n), |
H(z 1) |
|
|
a0 |
, H(z) |
a0 z |
. |
|
|
|
|
||||||
|
|
|
|
|||||
1 |
0 |
|
1 |
b z 1 |
z b |
|||
|
|
|
|
|
1 |
|
1 |
|
Полюс фильтра H0 (z) является единственным и может быть легко
найден: 1 |
b1. Воспользуемся уже выведенной формулой (6.1.8) |
||||||||||||||||
для связи выходного и входного сигнала |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
x(i) ( 1)i 1bi 1x( 1) |
( 1)i s bi sa y(s). |
||||||||||||
|
|
|
|
|
|
|
1 |
1 |
0 |
||||||||
|
|
|
|
|
|
|
|
|
s 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 и ограниченном |
||||||
Из анализа этой формулы следует, что при |
b1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
входном сигнале |
y(s) |
|
Y, s 0, 1,..., |
, всегда можно подобрать |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
X , |
обеспечивающее |
|
неравенство |
|
x(i) |
|
X для любых |
||||||||||
i |
0, 1,..., |
. Таким образом, для того, чтобы БИХфильтр первого |
|||||||||||||||
порядка оказался устойчивым, достаточно выполнение условия:
модуль полюса ПФ должен быть меньше единицы |
|
1 |
|
1 – лежать |
|
|
|||
внутри единичной окружности комплексной плоскости. |
|
|||
Разобранный пример позволяет сделать обобщение. Обратимся к выражению для ПФ произвольного БИХ-фильтра (6.2.5), рас-
смотрим формулу для H0 (z), сомножитель H0zm k не влияет на устойчивость. Положим, что у ПФ для H0 (z) нет кратных полюсов
189

и k m. Тогда можно записать разложение исходной ПФ в виде суммы ПФ-составляющих
m |
|
|
|
|
Br |
|
|
H0 (z) Bm 1 |
H0r (z), H0r (z) |
|
|
, |
|||
z |
|
|
|||||
r 1 |
|
|
|
|
r |
||
|
|
|
|
|
|||
|
m |
Br |
|
|
|
|
|
H0 (z) |
Bm 1 |
|
|
|
|
||
|
|
|
|
|
|
||
|
r 1 z r |
|
|
|
|
||
и выразить z-преобразование для выходного сигнала через сумму произведений z-преобразований входного сигнала и ПФ-со- ставляющих
|
m |
X0 (z) Bm 1Y(z) |
H0r (z)Y(z). |
|
r 0 |
Видно, что для обеспечения устойчивости рассматриваемого БИХфильтра достаточно выполнения условия: все модули полюсов для
ПФ-составляющих должны быть меньше единицы |
|
r |
|
1, |
|
|
 должны лежать внутри единичной окружности комплексной плоскости.
должны лежать внутри единичной окружности комплексной плоскости.
Сформулированное достаточное условие не позволяет определить устойчивость в критическом случае для полюсов, лежащих на единичной окружности.
Проделаем анализ на устойчивость БИХ-фильтра второго порядка, рассмотрим пример цифрового резонатора (колебательного звена). Воспользуемся разностным уравнением из (6.1.4)
x(i) b1x(i 1) b2x(i 2) a0 y(i).
Передаточная функция представляется следующим образом:
|
H(z |
1) |
|
|
|
|
a0 |
|
|
, |
|
|
|
||
|
1 |
b z |
1 |
b z 2 |
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
a z2 |
|
|
|
|
a z2 |
|
|
|
||||
H(z) |
|
|
0 |
|
|
|
|
= |
|
0 |
|
|
|
. |
|
|
z2 |
b z b z2 |
(z |
0 |
)(z |
1 |
) |
||||||||
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
||
Полюса этого БИХ-фильтра находятся из квадратного уравнения
2 |
b1 |
b2 |
0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
b1 |
1 |
|
|
|
|
|
|
|
0,1 |
b2 |
4b . |
||||
|
|
|
|
|
|||||
|
|
|
2 |
2 |
1 |
2 |
|
||
|
|
|
|
|
|
|
|
||
Чтобы фильтр был резонатором, необходима комплексная сопряжѐнность полюсов, которая достигается при выполнении условия
190
