
getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie
.pdf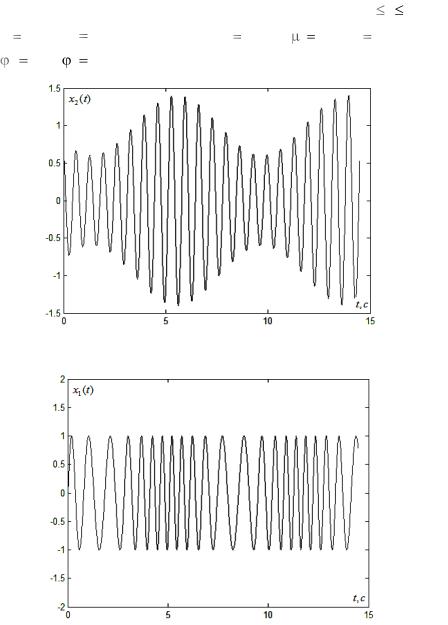
На рис. 2.1.3а изображена реализация сигнала с амплитудной
модуляцией, определѐнного на |
отрезке |
времени |
0 t t f , |
|||
t f 14,5 c, |
E 1, несущая частота f0 |
1,5 Гц, |
1 0,4, f1 |
0,12 Гц, |
||
0 |
0,5, |
1 |
2,1. |
|
|
|
|
|
|
|
|
||
Рис. 2.1.3а. Реализация сигнала с синусоидальной амплитудной модуляцией
Рис. 2.1.3б. Реализация сигнала с синусоидальной частотной модуляцией
41
Сигнал (2.1.5) может быть разложен на сумму трѐх гармониче-
ских составляющих сигналов с частотами |
0 , |
0 |
, |
0 |
, где |
||||||
0 2 f0 , |
2 f1. Положим для удобств выкладок, |
что |
0 0, |
||||||||
0, разложим произведение косинусов в сумму |
|
|
|
||||||||
x (t) |
E cos t |
E |
cos(( |
|
)t) |
|
E |
cos(( |
|
|
)t). |
|
0 |
|
|
0 |
|
||||||
1 |
0 |
2 |
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
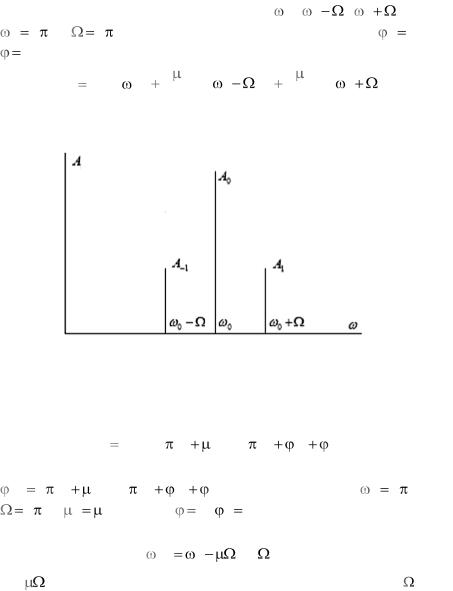
Амплитудный спектр сигнала с синусоидальной амплитудной модуляцией, изображѐн на рис. 2.1.4.
Рис. 2.1.4. Амплитудный спектр сигнала с синусоидальной амплитудной модуляцией
Гармонический сигнал с фазовой (частотной) синусоидальной модуляцией описывается выражением
|
|
x2 (t) Ecos(2 |
f0t |
|
2 sin(2 f2t |
2 ) 0 ). |
(2.1.6) |
||
Для |
(2.1.6) |
модулированная |
|
фазовая |
функция имеет |
вид |
|||
(t) |
2 f0t |
2 sin(2 f2t |
2 ) |
|
0 . Введѐм обозначения |
0 2 |
f0 , |
||
2 |
f2 , 2 |
, положим |
|
0, 0 0. |
Для сигнала (2.1.6) часто- |
||||
та модулируется по гармоническому закону |
|
|
|
||||||
|
|
(t) |
0 |
cos |
t, |
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
определяет амплитуду функции частотной модуляции; |
– |
|||||||
частота частотной модуляции. На рис. 2.1.3б представлен пример реализации модельного сигнала с частотной модуляцией,
42
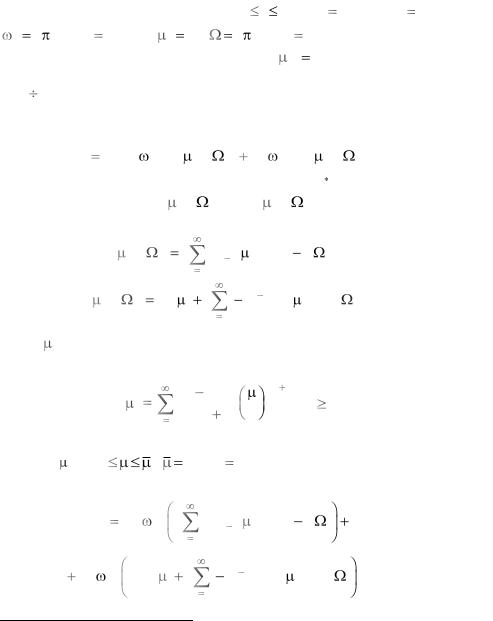
определѐнный |
на |
отрезке |
времени 0 |
t |
t f , |
t f |
14,5 c, |
E 1, |
||
0 2 |
f0 , f0 |
1,5 Гц, 2 |
4, |
2 |
f2 , |
f2 |
0,15. |
Глубина час- |
||
тотной |
модуляции |
составляет |
величину |
f2 |
0,6 Гц и |
частота |
||||
данного частотно-модулированного сигнала колеблется в пределах
(0,9 2,1) Гц.
Сигнал (2.1.6) может быть представлен в виде бесконечной суммы гармонических составляющих. Запишем (2.1.6) в виде
x2 (t) E(cos 0t sin( sin t) sin 0t cos( sin t). |
(2.1.7) |
Воспользовавшись работой Г.М. Фихтенгольца , разложим пе-
риодические функции sin( |
sin |
t) и cos( sin |
t) в ряд по синусам |
|||
и косинусам кратных дуг |
|
|
|
|
||
sin( |
sin |
t) |
2 |
J2l 1( )sin(2l |
1) t, |
|
|
|
|
l |
1 |
|
(2.1.8) |
|
|
|
|
|
|
|
cos( sin |
t) |
J0 ( |
) |
2 |
( 1)l 1 J2l ( |
)cos2l t, |
|
|
|
|
l |
1 |
|
где Jl ( ) – функции Бесселя первого рода порядка l, для которой справедливо разложение в степенной ряд
|
|
( 1)m |
|
|
2m l |
|
|
Jl ( ) |
|
|
, |
l 0. |
|||
m 0 m!(m l)! |
2 |
||||||
|
|
|
|||||
На рис. 2.1.5 представлены графики функции Бесселя в зависимости от для 0 , 15 и l 0, 1, 2.
Подставим в (2.1.7) выражения разложений (2.1.8), получим
x2 (t) сos 0t 2 |
ЕJ2l 1( )sin(2l 1) t |
l |
1 |
sin |
t ЕJ |
0 |
( ) 2 |
( 1)l 1ЕJ |
2k |
( )cos2l t . |
0 |
|
|
|
|
||
|
|
|
|
l 1 |
|
|
 Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.3. М.: Физматгиз. 1963. 656 с.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.3. М.: Физматгиз. 1963. 656 с.
43
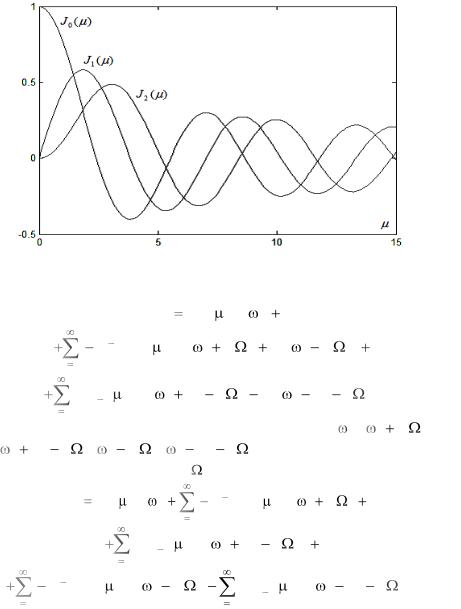
Рис. 2.1.5. Графики функций Бесселя первого рода
Сделаем очевидные преобразования
x2 (t) ЕJ0 ( )sin 0t
( 1)l 1ЕJ2l ( )[sin( 0 2l )t sin( 0 2l )t]
l 1
|
|
ЕJ2l 1( |
|
)[sin( 0 |
|
(2l |
|
1) |
)t |
|
sin( |
0 (2l |
1) |
)t] |
|
|||||
|
l |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и соберѐм гармонические составляющие с частотами |
0 , |
0 |
2l , |
|||||||||||||||||
0 |
(2l |
1) , |
0 |
|
2l |
, |
0 |
(2l |
1) , |
которые располагаются с |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дискретным шагом по частоте |
относительно несущей частоты |
|||||||||||||||||||
|
|
x (t) ЕJ |
0 |
( |
)sin |
t |
|
( |
1)l |
1ЕJ |
2l |
( )sin( |
0 |
2l |
)t |
|
|
|||
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
l |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЕJ2l 1( )sin( |
0 |
(2l |
1) |
)t) |
|
|
(2.1.9) |
|||||||
|
|
|
|
|
l |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1)l 1 ЕJ2l ( |
|
)sin( |
0 |
2l |
)t |
|
|
ЕJ2l 1( |
)sin( |
0 |
(2l |
1) |
)t). |
||||||
|
l 1 |
|
|
|
|
|
|
|
|
|
l |
1 |
|
|
|
|
|
|
|
|
Из (2.1.9) видно, что амплитуды гармонических составляющих определяются значениями функций Бесселя.
44
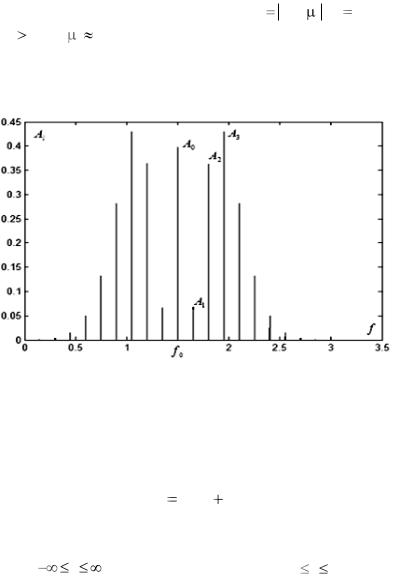
На рис. 2.1.6 представлен пример амплитудного спектра час- тотно-модулированного по синусоидальному закону сигнала вида (2.1.9), симметричного относительно f0, Al ЕJl ( ) , l 0, 1,..., 8;
для l 8, Jl ( ) 0. Из (2.1.9) можно заключить, что данный час-
тотно-модулированный сигнал допускает представление в виде полигармонического сигнала с достаточно широким спектром, который в данном случае состоит из 15 гармонических составляющих.
2.1.6. Амплитудный спектр сигнала с синусоидальной частотной модуляцией
2.2. Комплексные сигналы. Энергетические характеристики сигналов
Комплексные сигналы являются естественным обобщением действительных сигналов и записываются в виде
x(t) x1 (t) jx2 (t) ,
где x1(t), x2 (t) – действительная и мнимая составляющие комплексного сигнала x(t), которые определены на бесконечном ин-
тервале |
t |
или конечном интервале t0 t t f времени. |
Комплексные сигналы могут быть представлены в показательной форме
45

x(t) E(t)e j (t) , |
E2 (t) x2 |
(t) |
x2 |
(t), |
(t) arctg(x (t) / x (t)). |
|
|
1 |
|
2 |
|
2 |
1 |
В качестве примера комплексного сигнала приведѐм выражение для комплексной синусоиды с параметрами A, 0, 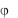
x(t) Ae |
j( |
0t |
) |
Acos( 0t ) j Asin( 0t ) . |
|
|
|
Для любого момента времени t значения комплексных сигналов x(t) представляют собой комплексные числа, над которыми можно
производить все операции комплексной арифметики. Использование комплексных сигналов доставляет определѐн-
ные математические удобства; в том числе основные соотношения ЦОС записываются в комплексной форме с целью обеспечения компактности формул. Многие распространѐнные программы вычислений, используемые для задач ЦОС, работают с комплексными входными и выходными данными.
Энергия E комплексного сигнала x(t), по определению, записывается в виде интеграла
E |
x*(t)x(t)dt |
(x2 |
(t) x2 |
(t))dt, |
|
|
1 |
2 |
|
где звѐздочка наверху * является знаком комплексного сопряжения. Данное определение энергии сформулировано в соответствии с аналогией из электротехники – величиной энергии, выделяемой на активном сопротивлении R при действии комплексного тока I(t)
E I*(t)I (t)Rdt.
Очевидно, что сигналы x(t), которые фигурируют в ЦОС, должны обладать конечной энергией
E |
x*(t)x(t)dt |
. |
Однако необходимо иметь в виду, что не все сигналы, фигурирующие в ЦОС, обладают конечной энергией; например, у периодических сигналов, очевидно, энергия бесконечна.
Средняя мощность P(T0, t) сигнала x(t) определяется энергией,
отнесѐнной к заданному интервалу времени Т0 :
46

1 t T0
P(T0, t) T0 t x*( )x( )d .
Мгновенная мощность сигнала P0 (t) в момент времени t определяется как предел
|
|
|
1 |
t |
T0 |
x*(t)x(t). |
P (t) lim |
|
x*( )x( )d |
||||
|
|
|||||
0 |
T0 |
0 |
T |
|
|
|
|
|
t |
|
|||
|
|
|
0 |
|
|
|
Средняя мощность действительного гармонического сигнала, определѐнного в разд. 2.1
x(t) Acos( 0t )
на интервале времени, который соответствует периоду T0 |
2 / 0, |
|
не зависит от начального момента времени t, частоты |
0 |
и началь- |
|
|
|
ной фазы , поскольку на таком интервале времени укладывается в точности одно колебание рассматриваемого гармонического сигнала. В самом деле, величина средней мощности гармонического сигнала может быть вычислена с помощью следующего интеграла
|
|
t |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
2 |
|
A2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 |
|
A2 cos2 ( 0 |
|
0 |
A2 |
|
1 sin 2( |
|
0 |
|
|||||
P |
|
|
|
)d |
|
|
) |
. |
||||||||
2 |
|
2 |
|
0 |
|
|||||||||||
|
|
t |
|
|
2 4 |
|
t |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Средняя мощность действительного полигармонического сигнала
|
L |
x(t) |
(al cos lt bl sin lt) |
l |
1 |
на отрезке времени Т0 должна представиться в виде интеграла
|
|
1 |
t |
T0 |
L |
2 |
P(T0 |
, t) |
|
|
(al cos l |
bl sin l d , |
|
|
|
|
||||
T0 |
|
|
||||
|
|
|
t |
l 1 |
|
который вычисляется достаточно сложным образом для произ-
вольных значений t, T0 |
и частот |
1,..., L. Рассмотрим частный |
|||||||
случай, |
когда |
частоты сигнала |
являются упорядоченными |
||||||
1 < 2 <...< |
L, |
kl и |
2,..., |
L кратны наименьшей частоте |
1. |
||||
Последнее означает, что существуют целые числа kl , |
l |
1,..., L, |
|||||||
k1 1 и |
kl 1 |
kl , которые |
обеспечивают равенства |
l |
kl |
1, |
|||
|
|
|
|
|
47 |
|
|
|
|
l 1,..., L, являющееся условием кратности для частот. Рассмотрим интервал интегрирования T0 2 / 1, равный наибольшему периоду для частот 1,..., L, составляющих полигармонического сигнала. Кратность указанных частот означает, что все составляющие
укладываются в точности целое число раз на времени Т0 |
и выпол- |
||||||
няются следующие равенства |
|
|
|
|
|
||
t T0 |
|
|
t T0 |
|
|
|
|
cos l |
cos l |
d 0, |
sin |
l |
sin l |
d 0, |
l1 l2; |
1 |
2 |
|
|
1 |
2 |
|
|
t |
|
|
t |
|
|
|
|
|
t |
T0 |
|
|
|
|
|
|
|
cos l |
sin l |
d |
0. |
|
|
|
|
1 |
2 |
|
|
|
|
t
Благодаря указанным равенствам для полигармонических составляющих следует, что средняя мощность P такого полигармониче-
ского сигнала равняется сумме средних мощностей P гармониче-
l
ских составляющих |
|
|
|
|
|
A2 |
|
|
L |
P |
l |
, l 1,..., L, |
P |
P . |
|
||||
l |
2 |
|
|
l |
|
|
|
l 1 |
|
|
|
|
|
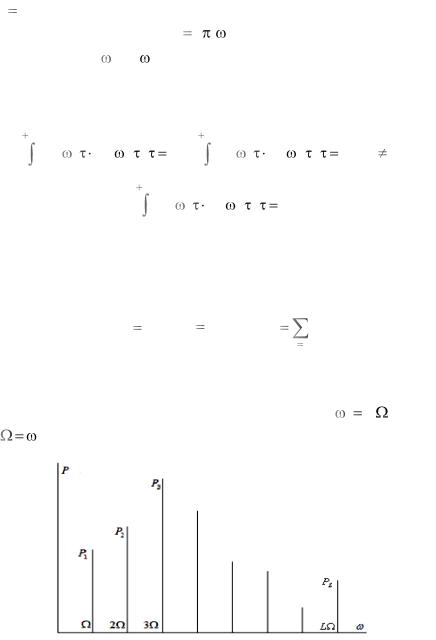
Для полигармонических сигналов с кратными частотами возможно наглядное представление дискретного спектра мощности сигнала в виде набора дискретных значений отдельных мощностей
Pl , соответствующих частотам составляющих |
1 kl , где |
1 (рис. 2.2.1).
Рис. 2.2.1. Дискретный спектр мощности
48

2.3. Наблюдения и модели сигналов |
|
|
||
Из |
разд. 1.1 |
(см. рис. 1.1.1) следует, |
что исходный |
сигнал |
x(t) |
x( p(t), t) |
определяется фазовыми |
координатами |
объекта |
управления и зависит от параметрической функции p(t). В параметрической функции p(t) содержится вся полезная информация
об объекте. Обычно должно выполняться соотношение |
p(t) P |
, |
|
0 |
|
где P0 – заданное множество, к которому принадлежат параметрические функции. Будем полагать, что наблюдаемый сигнал y(t)
связан с исходным сигналом x(t) |
x( p(t), t) и случайным помехо- |
||
вым возмущением |
w(t) через модельную функцию |
наблюдения |
|
h( , ) известного вида |
|
|
|
y(t) |
h(x(t), w(t)) |
h(x( p(t), t), w(t)). |
(2.3.1) |
В частном случае модельная функция наблюдения может быть аддитивной и представится выражением
y(t) x(t) w(t) x( p(t), t) w(t), |
(2.3.2) |
где w(t) – случайная погрешность наблюдения с заданными стати-
стическими характеристиками. Выражения (2.3.1), (2.3.2) являются моделями, по которым формируются наблюдения y(t). Для задач
ЦОС необходимо располагать видом функций h( , ), х( ,t) и статистическими характеристиками w(t), чтобы по наблюдениям y(t) осуществить определение оценок фазовых координат x (t) и параметрических функций p (t).
Наблюдения для задач цифровой обработки сигналов, как правило, задаются на конечном интервале времени в виде набора дискретных данных y(i), i 0, 1,..., N 1, N – число наблюдений. Ча-
ще всего наблюдения осуществляются через равные промежутки времени, y(i) y(Ti), T – интервал дискретизации; однако вполне
возможны ситуации, когда наблюдения производятся неравномерно во времени. Наблюдения, в общем случае, могут быть комплексными y(i) y1(i) jy2(i).
Математические модели сигналов должны соответствовать физическим сигналам, для описания которых они предназначены.
Выбор моделей зависит от объѐма и характера априорной инфор-
49

мации о физических сигналах. Будем рассматривать модели сигна-
лов двух типов – функциональные и параметрические.
Функциональная модель сигнала представляется соотношением вида
x |
( p,t) x |
( p(t), t), p(t) |
P . |
(2.3.3) |
M |
M |
|
0 |
|
Для модели (2.3.3) |
должна |
быть задана |
функция |
известного |
вида х( ,t), в которую осуществляется подстановка функций
p p(t) P . |
|
|
|
0 |
|
|
|
Параметрическая модель сигнала определяется функцией из- |
|||
вестного вида yМ (c, Ti), |
определѐнной на заданном конечном вре- |
||
менном интервале в точках i 0, 1,..., N |
1 и зависящей от вектора |
||
параметров cT (c ,..., c |
) размерности |
(m,1), служит в качестве |
|
1 |
m |
|
|
модели сигнала. Будем считать, что вектор с в общем случае при-
надлежит некоторому |
ограничивающему множеству |
Rm , |
||
|
|
|
|
0 |
c Rm |
Rm, иногда |
Rm |
Rm. Выбор вида функции модели про- |
|
0 |
|
0 |
|
|
изводится на основе априорных сведений о природе сигнала и объекта управления. Вектор параметров модели с назначается таким образом, чтобы модель на заданном временном интерва-
ле описывала с заданной точностью исходный сигнал x(Ti). Определение вектора с для модели yМ (c,Ti) реализуется на основе решения задачи аппроксимации наблюдений y(Ti) (приближения
наблюдений).
Рассмотрим некоторые примеры моделей, которые могут использоваться для задач цифровой обработки сигналов.
Узкополосному сигналу на малом интервале времени может быть поставлена в соответствие модель в виде кусочносинусоидальной функции
yM (c, Ti) acos Ti bsin Ti, i 0, 1,..., N 1, (2.3.4)
где сТ (a, b, ) – вектор параметров модели, имеющий размерность (3,1). Амплитуды a, b входят в выражение для модели линейно, частота нелинейно. Данная модельная функция имеет постоянную амплитуду и частоту. Разумеется, модельная функция (2.3.4) не в полной мере соответствует исходному узкополосному сигналу с переменной амплитудой и частотой; однако несоответствие мо-
50
