Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белгородский университет кооперации, экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie

.pdf

Скачиваний:

Добавлен:

18.03.2016

Размер:

6.41 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2412 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Модель (4.1.4) и функционал (4.1.5) могут быть представлены с использованием скалярных произведений

		N 1
y (c, Ti)	сТ	( , i), S(c, y)	(y(i) сТ ( , i))2. (4.1.7)
M
		i	0

Введем на основе материалов разд. 2.4 векторно-матричные обозначения для вектора наблюдений Y размерности (N, 1), вектора

параметров с размерности (2N												1, 1) и матрицы плана сигнала X
размерности (N, 2N 1) :
							y(0)				a0						T (		,0)


											a1
											a1						T (
				Y			y(1)	,					,		X		T (		,1)
				Y				,	c		aN 1		,		X
									c		aN 1
						y(N 1)					b1						T ( , N 1)
											bN 1
		1	,	cos	2		1 0,...,		cos	0	0,	sin			2	1 1,...,		sin		0	0
		1			2										2
		2				N									N
		2				N									N
		1	,	cos	2		1 1,...,		cos	0	1,	sin		2		1 1,...,		sin		0	1			,
		2	,	cos		N	1 1,...,		cos	0	1,	sin		N		1 1,...,		sin		0	1			,
		2				N								N
		1	,	cos	0		1,..., cos 0			(N 1),				sin		0	1,...,	sin		0		(N	1)
		2
где	0		2	(N		1) N.
	0
	Оптимизируемый квадратичный по															с	функционал S(c, Y) за-

пишется с помощью векторно-матричных обозначений в виде скалярного произведения, тождественно совпадающего с функциона-

лом (4.1.5), (4.1.7)

S(c, Y) (Y Xc)T (Y Xc).

Оценки параметров модели с , соответствующие задаче минимизации (4.1.6), могут быть вычислены с помощью формулы (2.4.7)

с(XT X) 1 XTY.

Рассмотрим скалярные произведения синусоидальных базисных функций l ( , Ti), l 0,..., 2N 1. Благодаря предложенному рас-

111

положению частот в модели введѐнные базисные функции являются ортогональными

N 1
	l	( , Ti)	l2 ( , Ti) 0, l1, l2 1,..., 2N 1 и	l1 l2.
i 0	1
i 0

В этом можно убедиться, если произвести вычисления скалярных произведений для базисных функций на основе использования табличных формул для тригонометрических сумм. В самом деле, вычислим скалярные произведения базисных функций для разных индексов

N 1 1

N 1

0, r

1,..., N

cos

sin

0 2

i 0

N 1

cos

ricos

si 0,

sin

risin

cos

risin

si 0

i 0

для r, s 1,..., N 1, r s.

Вычислим скалярные произведения базисных функций для одинаковых индексов:

	N 1										2
			l	(	, Ti)	l	(	, Ti)			2		,		l	1,..., 2N				1,
			l			l						l
	i	0
N 1	1 1		N		2	N 1				2				2				N
2				,	2			cos				licos				li			, l	1,...., N 1,
0	2 2	4		,	l			cos		N		licos			N	li	2		, l	1,...., N 1,
0					l
i 0						i	0
				N 1		2			2				N
	2				sin	2	lisin		2		li		N		,	l	1,...., N			1.
	2
	l N					N				N			2
	l N
				i	0
				i	0

Вследствие ортогональности введѐнных синусоидальных базисных функций матрица D ХТ Х размерности (2N 1, 2N 1) является диагональной:

	N	0			0			4	0			0
	N							4

	4							N
	4							N
	0		N		0			0	2			0
D							, D 1						.
D		2					, D 1			N			.
					0							0
	0	0		0	N			0	0		0	2
	0	0		0	2			0	0		0	N
					2							N
						112

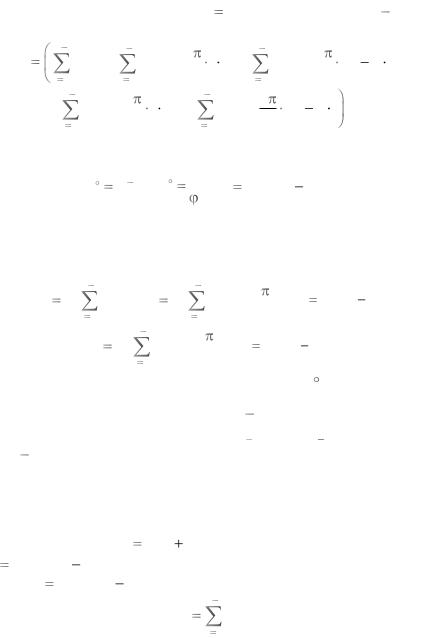
Вектор коэффициентов Фурье b XTY размерности (2N 1, 1) представляет собой набор скалярных произведений вида

N 1	1	N 1
bT		y(i),
i 0 2		i 0

	2	N 1		2
y(i)cos		1 i,...,	y(i)cos		(N 1) i ,
	N			N
		i	0

N 1

i 0

	2	N 1
y(i)sin		1 i ,…,
	N
		i 0

y(i)sin 2N (N 1) i .

Оптимальные параметры модели для ДПФ выразятся через коэффициенты Фурье

с D 1b,	c	bl	,	l 0,...,2N 1.	(4.1.8)
		2
	l

Основываясь на (4.1.8), запишем формулы, определяющие оптимальные параметры для модели (4.1.4) и являющиеся коэффициентами ДПФ для случая действительных наблюдений и действительной модели:

N 1

y(i),

2 N 1

y(i)cos

ki,

k 1,..., N

N i 0

N i

N 1

y(i)sin

ki,

1,..., N

(4.1.9)

N i 0

В формулах (4.1.9) опущен знак оптимальности

« ». В соответст-

вии с (4.1.9)

ДПФ осуществляет линейное преобразование вектора

наблюдений

сигнала

(y(0), y(1),..., y(N

1)) размерности

(N, 1) в

вектор параметров модели (a0, a1,..., aN 1, b1,..., bN 1) размерности

(2N 1, 1).

4.1.3. Дискретное преобразование Фурье для комплексных сигналов

Обобщим ДПФ, предложенное в разд. 4.1.2, для комплексных

сигналов.	Пусть	y(i) y1(i) jy2 (i)	– комплексные наблюдения,
i 0, 1,..., N 1.		Введѐм комплексную модель для наблюдений в
точках i	0, 1,..., N 1
		N 1	c(k)W ki .
		y (c, Ti)	c(k)W ki .
		M
		k 0
		113

Для этой модели c(k) c1(k) jc2 (k) – комплексные параметры, W – корень N-й степени из единицы, Wki – комплексные базисные

функции,

0, 1,..., N

1, i

0, 1,..., N

e j

cos

j sin

Wki

cos

j sin

ki,

k, i

0, 1,..., N

Функционал

S(c, Y) – мера близости комплексных наблюдений и

модели, запишется с помощью суммы комплексно-сопряженных сомножителей

N 1	N 1		*	N 1
N 1	N 1			N 1
S(c, Y)	y(i)	c(k)W ki		y(i)	c(k)W ki . (4.1.10)
i 0	k	0		k	0

Введѐм комплексные векторно-матричные переменные – вектор комплексных наблюдений Y размерности (N, 1), вектор c комплексных параметров модели размерности (N, 1) и комплексную матрицу плана сигнала X размерности (N, N):

		y(0)					c(0)
		y(0)					c(0)
	Y	y(1)			,	c	c(1)	,
	Y				,	c		,
		y(N		1)			c(N 1)
	W 0 0			W1 0			W (N 1) 0
	W 0 0			W1 0			W (N 1) 0
X	W1 0			W11			W (N 1) 1
X									.
									.
	W 0 (N 1)		W1 (N 1)				W(N 1)(N 1)

С учѐтом сопряжѐнности, основываясь на (2.4.9), запишем выражение для оптимальных оценок параметров

с(X*Т X) 1 X*Т Y.

Матрица D X*T X и вектор коэффициентов Фурье b X*T Y выразятся с использованием комплексных сопряжений. Коэффициенты ДПФ находятся из системы Dc b, с D 1b.

Базисные комплексные синусоидальные функции Wki ортогональны, и поэтому матрица D диагональна. Вычислим коэффициенты этой матрицы, сформировав тригонометрические суммы, являю-

114

щиеся скалярными произведениями для столбцов комплексной матрицы плана сигнала:

N 1

(Wki )*W si

W(s k)i ,

k, s

0,..., N

i 0

Для индексов s

k имеем dkk

для s

k следует,

что dks 0.

Тогда нетрудно видеть, что

N 1

y(i)W 0 i

N 1

y(i)W

D 1

X* Y

N 1

y(i)W (N 1)i

i 0

c (k) dkk bk , k 0, 1,..., N 1.

Коэффициенты ДПФ для случая комплексных наблюдений и комплексной модели запишутся следующим образом:

	1 N 1
c(k)		y(i)W ki , k 0, 1,..., N 1,.	(4.1.11)
	N i
		0

где так же, как и в (4.1.9), опущен знак оптимальности.

Вычислим остаточную сумму для оптимальных коэффициентов комплексного ДПФ. Подставим под знак суммы (4.1.10) полученные выражения для коэффициентов с(k) :

	N 1	N 1	1 N 1		*
	N 1	N 1	1 N 1
S(c, Y)	y(i)			y(s)W si W ki
S(c, Y)	y(i)			y(s)W si W ki
	i 0	k 0	N s 0
	N 1	1 N 1	y(s)W si W ki .
	y(i)
	y(i)	N s 0
	k 0	N s 0

Рассмотрим отдельно выражение в скобках под знаком суммы, переставим порядки суммирования, учитывая, что

N 1	N 1
W k(i s) N для s i,	W k(i s) 0 для s i,
k 0	k 0

115

N 1	1	N 1			1 N 1	N 1
y(i)		y(s)W ksW ki		y(i)		y(s) W k(i s)
y(i)		y(s)W ksW ki		y(i)		y(s) W k(i s)
k 0	N s 0				N s 0	k 0
		y(i)	1	y(i) N 0.
		y(i)	N	y(i) N 0.
			N

Нетрудно видеть, что имеет место равенство S(c , Y) 0. Остаточ-

ная сумма для функционала (4.1.10) на оптимальных коэффициентах ДПФ равняется нулю – предлагаемая тригонометрическая модель с нулевой погрешностью аппроксимирует наблюдения. Благодаря этому обстоятельству можно записать формулы прямого и обратного дискретного преобразования Фурье, физический смысл которых очевиден

	1 N 1		N 1
c(k)		y(i)W ki , k	0, 1,..., N 1, y(i)	c(k)Wki ,
c(k)	N i	y(i)W ki , k	0, 1,..., N 1, y(i)	c(k)Wki ,
	N i	0	k	0
		i	0, 1,..., N 1.

Приведѐм показательную форму для комплексного ДПФ. Опре-

делим амплитуды

с(k)

и фазы

(k) составляющих ДПФ в зависи-

мости от дискретного номера k:

c(k) c (k)

jc (k),

c(k)

e j k ,

с(k)

(c2(k)

(k))1/2,

(k) arctg(c (k)/c (k)), k 0, 1,..., N 1.

Результаты вычисления составляющих ДПФ можно графически изображать в виде амплитудного и фазового спектров. Для удобств изображений амплитудных спектров применяется логарифмический масштаб:

L с(k) 20log10 c(k) .

Вполне правомерно введение зависимости от частоты для составляющих спектра ДПФ. Шаг дискретности по частоте для составляющих определяется интервалом наблюдения NT, 2 /NT,

f 1/NT. Составляющие спектра – амплитуды и фазы модельных комплексных синусоид – располагаются равномерно по оси частот,

с(k)

c( k )

с(k)

c( fk )

(k)

(

k ),

(k)

( fk ) , где так

же, как и разд. 4.1.2, k

f k,

0, 1,..., N 1.

Рассмотрим пример вычисления амплитудного и фазового спектра ДПФ для сигнала в виде единичного прямоугольного импульса:

116

y(i) 1 для 0 i N0 1, y(i) 0 для N0 i N 1. (4.1.12)

Нахождение ДПФ для данного сигнала сводится к суммированию комплексной геометрической прогрессии со знаменателем W k :

N0 1

1 1 W kN0

kN0

KN0

1 W

W 2

c(k)

1 W ki

1 W k

i 0

W 2

0, 1,..., N

Cделаем необходимые выкладки, чтобы получить формулы для значений амплитудного и фазового спектров

kN0

sin

N0k

1 W

W 2

sin

W 2

sin

N0k

с(k)

(k)

kN0

(1 N0 )k ,

sin

0, 1,..., N

(4.1.13)

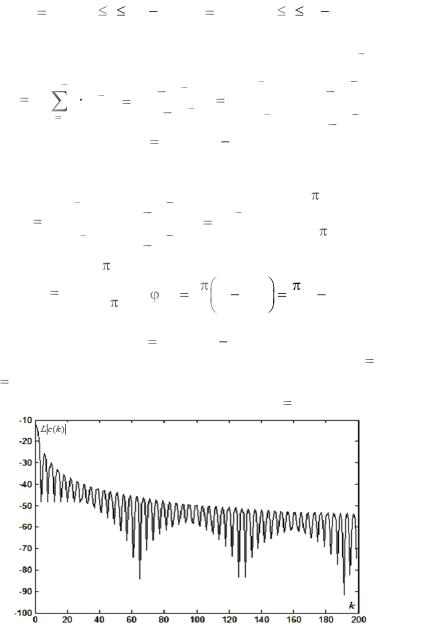
Для расчѐтов c(k)

по формулам (4.1.13)

взяты значения N 512,

N0 126. На рис. 4.1.1 изображен логарифмический амплитудный

сигнала (4.1.12) для точек k

0, 1,..., 199.

спектр ДПФ L

c(k)

Рис. 4.1.1. Логарифмический амплитудный спектр ДПФ для прямоугольного импульса

117

В практике обработки дискретных наблюдений, как правило, приходится иметь дело с действительными сигналами. Однако многие программы алгоритмов вычисления коэффициентов ДПФ ввиду определѐнных удобств записываются в комплексной форме. Чтобы можно было воспользоваться этими программами для вычисления ДПФ действительных сигналов, необходимо положить в комплексных наблюдениях мнимую составляющую, равную нулю:

y(i) y1(i) j 0, y2 (i) 0, i 0, 1,..., N 1.

Для комплексного сигнала с нулевой мнимой составляющей проведѐм вычисления коэффициентов ДПФ, получим

	1 N 1		2		1	N 1	2
c (k)		y (i)cos		ki, c (k)		y (i)sin		ki,
c (k)		y (i)cos		ki, c (k)		y (i)sin		ki,
1	N i 0	1		2		1
	N i 0		N		N i 0		N

k 0, 1,..., N 1.

Коэффициенты комплексного и действительного ДПФ связаны простыми соотношениями, которые следует применять для пересчѐта:

a k 2c1 (k) , k 0,1,...,N 1, bk

2c2 (k) , k 1,...,N 1.

4.2. Свойства дискретного преобразования Фурье

4.2.1. ДПФ для комплексной экспоненциальной функции

Необходимость вычисления дискретного преобразования Фурье для комплексной экспоненциальной функции может возникать для многих задач ЦОС.

Комплексная экспоненциальная функция определяется в дис-

кретных точках i 0, 1,..., N	1 с помощью формулы
y(i)	Ae j(2	fTi ) ,	(4.2.1)
где A – амплитуда; f – частота, Гц;		– начальная фаза; T – интервал

дискретизации; NT – длительность интервала наблюдения. Величина T0 1 f является периодом рассматриваемой функции. Возможно представление (4.2.1) в эквивалентном виде:

y(i) Acos(2 fTi ) jsin(2 fTi ), i 0, 1,..., N 1.

Вычисление ДПФ для (4.2.1) может быть реализовано на основе суммирования с применением табличных тригонометрических формул

118

c(k) c1(k) jc2 (k)

=	1 N 1	(Acos(2 f Ti ) jAsin 2 f Ti	cos	2	ki	j sin	2	ki ,

	N i 0			N			N

c (k)

1 N 1

Acos(2

fTi

)cos

Asin(2

fTi

)sin

ki ,

N i 0

c (k)

1 N 1

Acos(2

fTi

)sin

Asin(2

fTi

)cos

ki .

N i 0

Вычисление ДПФ для комплексной экспоненциальной функции может быть произведено с помощью суммирования специально сформированной геометрической прогрессии. Введѐм параметр q, равный числу периодов функции (4.2.1), укладывающихся на интервале наблюдения, и приведѐм очевидные равенства

q	NT	NT	f NT, fT	q	, 2 fTi	2	qi,	e j2 fTi	Wqi.
	T0	1/ f		N		N

Функция (4.2.1) может быть записана с учѐтом последнего равенства следующим образом:

y(i) Ae j(2 fTi ) Ae j e j2 fTi Ae j W qi , i 0, 1,..., N 1.(4.2.2)

Для y(i) в форме (4.2.2) нахождение коэффициентов с(k) ДПФ сводится к вычислению суммы N членов комплексной геометриче-

ской прогрессии со знаменателем Wq k
	1		N 1				1		N 1
с(k)			Ae j WqiW			ki			Ae j	W(q k)i

	N i 0							N	i 0
	1		Ae j	1	W (q k)N		, k 0, 1,..., N			1.
		N		1	W q k

Воспользуемся приѐмом, который был ранее использован в (4.1.12), сделаем необходимые преобразования для с(k) :

(q k)N

с(k)

1 Ae j 1 W

(q k)N

1 Ae j

1 W q k

q k

W 2

Получим амплитудные

с(k)

и фазовые (k) зависимости для дан-

ного ДПФ, k

0, 1,..., N

119

(q k)N

c(k)

q k

W 2

k)N

sin N

sin

(4.2.3)

sin 2

sin

k)N

2 (q k)N 2 (q k)

(k)

arg

W 2

(4.2.4)

Вычисление

модулей

нормированных

коэффициентов

ДПФ

c0(k)

c(k)

N удобно проиллюстрировать с помощью аппарат-

ной функции u(

q, q0,

k), которая образуется на основе (4.2.3):

q, q0 ,

sin

(q0

0, 1,..., N

sin

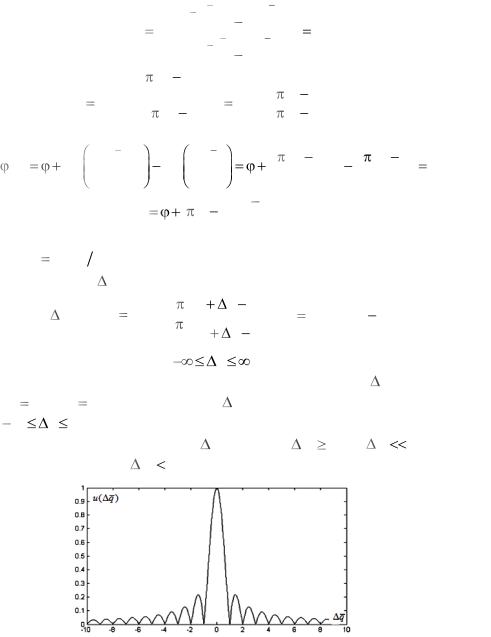
На рис. 4.2.1 изображѐн график

аппаратной функции u( q) при

q0 k,

512

и переменная

удовлетворяет неравенству

10. Нетрудно убедиться в том,

что аппаратная функция

быстро уменьшается с ростом q; так,

при

10 и

значения функции u( q)

0,05 становятся существенно малыми.

Рис. 4.2.1. График аппаратной функции

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2412 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>