
getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie
.pdf
i 0, i N2. Апериодическая свѐртка определяется следующим выражением
|
i |
|
x(i) |
h(i s)y(s), i 0, 1,..., N1 N2 2. |
(5.3.1) |
s |
0 |
|
На рис. 5.3.1 схематически изображена процедура вычисления апериодической свѐртки, основанный на движении вправо графика функции h(i s) за счѐт увеличения индекса i.
Рис. 5.3.1. Процедура вычисления апериодической свѐртки
Последовательность x(i) определена в N1 N2 1 точках. Если раскрыть выражение для апериодической свѐртки, то из представ-
ления суммы x(i) h(i)y(0) |
h(i |
1)y(1) ... h(0)y(i) |
следует воз- |
||
можность следующей записи: |
|
|
|
|
|
|
i |
|
|
|
|
x(i) |
|
h(s)y(i s). |
|
|
|
|
s |
0 |
|
|
|
Апериодические свѐртки могут быть сведены к круговым. Вве- |
|||||
дѐм последовательности h1(i), y1(i), определѐнные в N1 |
N2 1 |
||||
точках: |
|
|
|
|
|
h1(i) h(i), 0 i N1 1, h1(i) 0, N1 |
i N1 |
N2 |
2, |
||
y1(i) y(i), 0 i N2 |
1, y1(i) 0, N2 |
i N1 |
N2 |
2. |
|
|
171 |
|
|
|
|

Периодически продолжим последовательности h1(i), y1(i) с периодом N1 N2 1. После доопределения можно убедиться в справед-
ливости записи исходной апериодической свѐртки в форме круговой:
N1 N2 2
x1(i) |
h1(i s)y1(s), i 0, 1,..., N1 N2 2, |
s |
0 |
и возможности равенства x1(i) x(i).
Сведение апериодических свѐрток к круговым в ряде случаев не всегда удобно реализовывать, когда длина одной последовательности много больше длины другой, например при N2 N1. Разобьѐм
интервал определения свѐртки на некоторое число состыкованных участков – локальных интервалов, и вычислим основную свѐртку по частям – осуществим секционирование свѐртки. Положим, что N1 N2 1 Nm, m – число локальных интервалов; N – число то-
чек на локальном интервале. Последовательность y1(i) разобьѐм на сумму m подпоследовательностей y1 j (i), j 1,..., m:
y1 j (i) y1(i), N( j 1) i Nj 1, y1 j (i) 0, i N( j 1), i Nj 1.
Благодаря такому определению входная последовательность может быть сформирована в виде суммы
m
y1(i) |
y1 j (i). |
j |
1 |
Выпишем выражение для образующихся секционированных свѐрток
|
Nj 1 |
xj (i) |
h1(i s)y1 j (s), i N( j 1),..., Nj 1 N1, |
|
s N( j 1) |
|
j 1,..., m. |
Получим окончательный результат – апериодическая свѐртка представляется суммой перекрывающихся свѐрток
m
x(i) |
x j (i), i 0, 1,..., N1 N2 2. |
j |
1 |
|
172 |
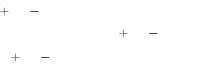
Вычисление xj (i) сводится к короткой круговой свѐртке размерности N N1 1, нахождение x(i) эквивалентно вычислению m круговых свѐрток длиной N N1 1 точек. Видно, что xj (i) определена в N N1 1 точках, тогда как подпоследовательность y1 j (i)
имеет длину N, поэтому суммирование при вычислении исходной свѐртки осуществляется с «перекрытием».
Список вопросов для самопроверки к гл. 5
1.В чѐм состоит определение для круговых свѐрток?
2.Каким образом реализуется вычисление круговых свѐрток на круговой диаграмме?
3.Каким образом вычисление круговых свѐрток сводится к вычислениям ДПФ?
4.В чѐм состоит отличие определения для апериодических свѐрток от определения круговых вѐрток?
5.Каким образом вычисление апериодических свѐрток сводится
квычислению круговых свѐрток?
6.Каким образом реализуется секционирование апериодических свѐрток?
173

Глава 6. ЦИФРОВАЯ ФИЛЬТРАЦИЯ СИГНАЛОВ
6.1.Разностные уравнения и импульсно-переходные функции цифровых фильтров
6.1.1. Разностные уравнения цифровых фильтров
Разностные уравнения для цифровых фильтров (ЦФ) задаются соотношениями типа
m |
|
k |
|
x(i) |
br x(i r) |
as y(i s), i 0, 1, 2... . |
(6.1.1) |
r 1 |
s |
0 |
|
В соответствии с (6.1.1), ЦФ осуществляют линейное преобразова-
ние |
входного сигнала |
в виде скалярной последовательности |
|||
y(i) |
y(Ti), определѐнной для дискретных индексов k |
i |
, |
||
в выходной сигнал в |
виде последовательности x(i) |
x(Ti) |
, |
||
m |
i |
. Здесь T – интервал дискретизации, хотя в явном виде |
|||
разностные уравнения (6.1.1) не зависят от T.
ЦФ полностью определяется набором коэффициентов разностного уравнения – весовыми параметрами b1,b2 ,...,bm , a0 , a1,...,ak ,
и, как следствие, целыми числами m, k , которые задают порядок ЦФ. Формирование выходной последовательности начинают с дис-
кретного индекса i |
0 . Значение х(0) вычисляется на основе m |
||||||
начальных |
условий |
для входной |
последовательности |
x( |
1), |
||
x( 2),..., x( |
m) |
и k |
1 значений |
входной последовательности |
|||
у(0), y( 1),..., y( |
k); |
х(1) для n 1 вычисляется на основе m зна- |
|||||
чений входной последовательности х(0), x( 1),..., x( m |
1) и k |
1 |
|||||
значений входной последовательности у(1), у(0),..., y( k |
1) |
и т.д. |
|||||
Выходной сигнал ЦФ (6.1.1) состоит из суммы сдвинутых и взвешенных значений входного сигнала – скользящего среднего входного сигнала и обратной связи – суммы сдвинутых и взвешенных значений выходного сигнала.
ЦФ делятся на два класса. К первому классу относятся нерекурсивные цифровые фильтры (НРЦ-фильтры) или фильтры скользя-
174

щего среднего, разностные уравнения для которых представляются соотношением
|
k |
|
x(i) |
as y(i s), i 0, 1, 2... . |
(6.1.2) |
s |
0 |
|
Сигнал с выхода таких фильтров не зависит от обратной связи. Ко второму классу относятся рекурсивные цифровые фильтры (РЦфильтры), являющиеся фильтрами общего вида, разностные уравнения для которых определены в (6.1.1); для этих фильтров выходной сигнал зависит от сигнала обратной связи. Следует отметить один частный вид РЦ-фильтров без скользящего усреднения
|
m |
x(i) |
br x(i r) a0 y(i), i 0, 1, 2... . |
r1
Вкачестве примера приведѐм разностное уравнение ЦФ первого порядка в виде цифрового апериодического звена
x(i) b1x(i 1) a0 y(i) (6.1.3)
и разностное уравнение ЦФ второго порядка в виде колебательного звена – цифрового резонатора
x(i) |
b1x(i 1) b2x(i 2) a0 y(i). |
(6.1.4) |
На рис. 6.1.1а приведена иллюстрация выходного сигнала фильтра первого порядка (6.1.3) при действии входного единичного ступенчатого воздействия, полученная в результате математического мо-
делирования. |
Для расчѐта брались значения a0 |
0,15; b1 |
0,75; |
||
y(i) |
1 для i |
0, 1,..., 19 . Начальное условие x( |
1) 0,133. Видно, |
||
что |
дискретные значения |
выходного сигнала |
фильтра |
x(i) для |
|
i 0, 1,..., 19 |
стремятся |
асимптотически к величине |
y1( ) |
||
a0 / (1 b1) |
0,15 / (1 0,75) 0,6. Рис. 6.1.1б содержит изображе- |
||||
ние выходного сигнала фильтра второго порядка (6.1.4) при дейст-
вии единичного воздействия |
y(i) |
1 для i 0, 1,..., 34. |
При моде- |
||||
лировании |
для |
параметров |
фильтра были |
выбраны |
значения |
||
а0 0,55 и |
b1 |
0,95; b2 |
0,75, |
начальные |
условия |
– x( 1) |
|
0,354; |
x( 2) |
1,6367. |
Выходной сигнал |
x(i), i |
0, 1,..., 34, |
||
представляет собой дискретные затухающие колебания, которые
стремятся |
асимптотически |
к |
постоянной величине y2 ( ) |
a0 / (1 b1 |
b2 ) 0,55 / (1 |
0,95 |
0,75) 0,203. |
|
|
175 |
|

Рис. 6.1.1а. Выход ЦФ первого порядка при действии ступенчатого единичного входного сигнала
Рис. 6.1.1б. Выход ЦФ второго порядка при действии ступенчатого единичного входного сигнала
Возможно дальнейшее обобщение для ЦФ, когда входная y(i) и выходная x(i) последовательности являются векторами размерности q, p а весовые параметры – матрицами Br , As размерности
( p, p), ( p, q):
176

|
y (i) |
|
|
x (i) |
|
b11,r |
b12,r |
b1p,r |
|
||||
|
|
|
|
|
|||||||||
|
|
|
|
||||||||||
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
y(i) |
y2 (i) |
, x(i) |
|
x2 (i) |
, B |
b21,r |
b22,r |
b1p,r |
, |
||||
|
... |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yq (i) |
|
|
xp (i) |
|
b |
p1,r |
b |
p2,r |
b |
pp,r |
|
|
|
|
|
a11,s |
a12,s |
|
|
a1q,s |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
A |
a21,s |
a22,s |
|
|
a1q,s |
. |
|
|
|
||
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aq1,s |
aq2,s |
|
|
aqq,s |
|
|
|
|
||
Векторно-матричный фильтр записывается с использованием введѐнных обозначений
m |
|
k |
x(i) |
Br x(i r) |
As y(i s), i 0, 1, 2... . |
r 1 |
s |
0 |
Очевидно, любой рекурсивный скалярный фильтр общего вида с помощью новых обозначений для сдвинутых переменных может быть записан в матрично-векторной форме. Действительно, для
примера |
(6.1.4) |
введѐм |
новые |
переменные |
x1(i) |
x(i), |
|
x (i) |
x(i |
1) и |
вектор |
xT (i) (x (i), x (i)), тогда |
x (i |
1) |
|
2 |
|
|
|
1 |
2 |
2 |
|
x(i |
2) и ЦФ (6.1.4) может быть переписан в виде дискретной |
||||||
системы
x1(i) b1x1(i 1) b2x2 (i 1) a0 y(i), x2 (i) x1(i 1). (6.1.5)
Система (6.1.5), в свою очередь, может быть представлена в виде матричновекторного ЦФ первого порядка
|
|
|
|
|
|
|
|
В |
b1 |
b2 |
, А |
a0 |
, |
x(i) В x(i 1) А y(i). |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
|
|
|
|
|
|||
6.1.2. Импульсно-переходные функции ЦФ
Импульсно-переходные функции ЦФ, зависящие от целочисленных аргументов, позволяют без обратной связи, напрямую, связать значения входного сигнала с выходным. Рассмотрим общий вид ЦФ (6.1.1) в виде РЦ-фильтра. Заметим, что РЦ-фильтр является линейной структурой: если проследить по формулам (6.1.1) образование выходного сигнала для i-го момента, начиная с
177

i 0, 1, 2, ..., то нетрудно понять, что для РЦФ выходной сигнал x(i) представляется в виде некоторой линейной комбинации значений начальных условий x( 1), x( 2),..., x( m) и последовательно-
сти входного сигнала y(i), y(i 1),..., y(0), y( 1), у( 2),..., y( k).
Введѐм весовые коэффициенты h(i, s), h0 (i, r), которые всегда
можно определить из разностных уравнений в виде громоздких зависимостей от целочисленных переменных i, s, r. Запишем выходной сигнал РЦФ x(i) с использованием взвешенных сумм
m |
i |
|
|
x(i) |
h0 (i,r)x( r) |
h(i, s)y(s). |
(6.1.6) |
r |
1 |
s k |
|
Функции двух переменных h(i, s), определѐнные в дискретных
точках, обычно называются импульсно-переходными. Необходимо, однако, иметь в виду, что выходной сигнал x(i) зависит от функ-
ции h(i, s) и функции h0 (i, r), учитывающей вклад начальных ус-
ловий. Если начальные условия являются нулевыми, то формула связи (6.1.6) упрощается:
|
i |
|
x(i) |
h(i,s)y(s). |
(6.1.7) |
s k
Таким образом, основываясь на (6.1.6), (6.1.7), выходной сигнал ЦФ с помощью импульсно-переходной функции может быть напрямую связан со входным сигналом.
Рассмотрим вычисление импульсно-переходной функции для рекурсивного скалярного фильтра первого порядка
|
x(i) |
|
b1x(i 1) a0 y(i). |
|
|
|||||||
Выразим x(0) через x( |
1), y(0), затем x(1) |
через x( |
1), |
y(0), y(1) |
||||||||
и т.д.: |
|
|
|
|
|
|
|
|
|
|
|
|
|
x(0) |
|
b1x( 1) |
a0 y(0), |
|
|
||||||
x(1) |
b1x(0) a0 y(1) |
|
b1 ( |
b1x( 1) |
a0 y(0)) |
a0 y(1) |
||||||
|
b2x( 1) |
b a y(0) |
|
a y(1) , |
|
|
||||||
|
1 |
|
|
1 |
0 |
|
|
|
0 |
|
|
|
x(2) b x(1) a y(2) |
b |
(b2x( |
1) |
b a y(0) a y(1)) |
a y(2) |
|||||||
1 |
0 |
1 |
|
1 |
|
|
|
1 |
0 |
0 |
|
0 |
|
b2x( 1) |
b2a y(0) |
b a y(1) a y(2), |
|
|
|||||||
|
1 |
1 |
|
0 |
|
|
1 |
0 |
|
0 |
|
|
…
178

Из приведѐнных выкладок заключаем, что для i-го шага справедливо выражение, позволяющее вычислить значение x(i) через на-
чальное условие x( 1) и входную последовательность y(0), y(1),..., y(i):
|
i |
|
|
x(i) ( 1)i 1bi 1x( 1) |
( 1)i s bi |
sa y(s). |
(6.1.8) |
1 |
1 |
0 |
|
s |
0 |
|
|
Исходя из (6.1.8) можно записать формулу для импульсно-
переходной |
функции h(i, s) |
( 1)i s bi |
sa |
и функции h (i,1) |
|
|
1 |
0 |
0 |
( 1)i 1bi 1. |
Очевидно, что |
нахождение |
импульсно-переходных |
|
1 |
|
|
|
|
функций для ЦФ порядка выше первого сопряжено со сложными выкладками. Для векторно-матричной формы ЦФ первого порядка вывод, аналогичный (6.1.8), не должен измениться:
|
n |
|
|
x(i) ( 1)i 1Bi 1x( 1) |
( 1)i s Bi |
s A y(s). |
(6.1.9) |
1 |
1 |
0 |
|
i |
0 |
|
|
Из (6.1.8), (6.1.9) следует, что импульсно-переходные функции зависят от разности аргументов
h(i, s) ( 1)i s bi sa h(i s) |
|
1 |
0 |
и могут быть представлены как функции одного положительного целочисленного аргумента h(m), m 0, 1, 2,... . Выходной сигнал
рекурсивного фильтра представляется в виде свѐртки. При нулевом начальном условии справедлива компактная запись для выходного сигнала
|
i |
i |
|
x(i) |
h(i s)y(s) |
h(s)y(i s). |
(6.1.10) |
s |
0 |
s 0 |
|
Из (6.1.10) видно, что импульсно-переходная функция фильтра при нулевых начальных условиях тождественно равна реакции фильтра на импульсное единичное входное воздействие:
y(i) 1, i 0, y(i) 0, i 0, x(i) h(i).
Для импульсно-переходных функций НРЦ-фильтров, с учетом формул (6.1.10), нетрудно убедиться, что справедливы следующие равенства:
|
k |
x(i) |
as y(i s), h(0) a0, h(1) a1,..., h(k) ak . |
s |
0 |
|
179 |

В данном случае импульсно-переходные функции определены в конечном числе точек. Фильтры, имеющие такие импульснопереходные функции, называются КИХ-фильтрами. РЦ-фильтры имеют импульсно-переходные функции, определѐнные в бесконечном числе точек; такие фильтры называются БИХ-фильтрами.
6.2. Передаточные функции и условие устойчивости для ЦФ
6.2.1. Передаточные функции для ЦФ
Передаточные функции (ПФ) для ЦФ определяются его выходным сигналом в установившемся режиме при действии на входе фильтра единичного дискретного комплексного синусоидального сигнала
|
|
y(Тi) e j Ti , 0 i |
, |
где T |
– |
интервал дискретизации, частота |
входного сигнала – |
2 |
f . |
В установившемся режиме выходной сигнал ЦФ пред- |
|
ставляет собой комплексную синусоидальную функцию с частотой входной синусоиды и отличающуюся от входной синусоиды амплитудными и фазовыми искажениями, которые зависят от частоты. Проиллюстрируем этот факт с помощью математического моделирования. Рассмотрим ЦФ первого порядка в виде цифрового апериодического звена (6.1.3) со входным сигналом в виде синусоиды
|
|
x(i) b1x(i |
1) |
a0 y(Тi), y(Ti) |
Asin(2 |
fTi ), |
|
|
|
|
|
i |
0, 1,..., N |
1. |
|
|
(6.2.1) |
Для |
расчѐтов брались значения параметров фильтра a0 |
0,15; |
||||||
b1 |
0,55, |
начальное |
условие x( 1) |
2,636; T |
0,01; |
N 80; |
||
A |
1; f |
5,0 Гц; |
/2. На рис. 6.2.1 |
пунктирной линией изо- |
||||
бражѐн вычисленный входной синусоидальный сигнал y(Ti), время наблюдения составляет величину T(N 1) 0,79 c, сплошной линией изображѐн вычисленный выходной сигнал ЦФ x(i) x(Ti).
Видно, что после непродолжительного переходного процесса наступает установившийся режим – на выходе ЦФ формируется установившийся синусоидальный сигнал
0 ) с частотой входного сигнала и с амплитудными и фазовыми искажениями. Из анализа графика выходного сигнала можно
180
