
getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie
.pdf
Аппаратная функция может быть представлена в зависимости от
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
частотного параметра |
|
|
f в виде u( f ); очевидно, |
для f |
10 f , |
||||||||||||||
где |
|
f |
– шаг дискретности по частоте, должно выполняться нера- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
венство |
u( f ) |
0,05. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
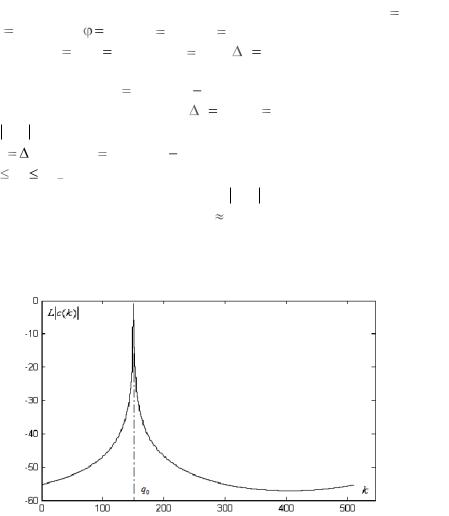
На рис. 4.2.2 помещѐн график для вычисления нормированных |
||||||||||||||||||
коэффициентов ДПФ |
|
c0 (k) |
|
, для примера взяты численные значе- |
|||||||||||||||
|
|
||||||||||||||||||
ния N |
512, q0 |
4, |
|
q 0,25. На этом графике представлена ап- |
|||||||||||||||
паратная функция, смещѐнная вправо на величину |
q0 |
q. Значе- |
|||||||||||||||||
ния |
|
c0 (k) |
|
отмечены жирными точками и пунктирными линиями, |
|||||||||||||||
|
|
||||||||||||||||||
которые соответствуют целочисленным k. Ясно, что |
максимальное |
значение модуля коэффициента ДПФ приходится на номер k q0. |
|
Очевидно, что при |
q 0 и k |
|
q0 |
4 модуль коэффициента ДПФ |
||||||
|
с(4) |
1; для k 4 |
с0(k) |
|
0 – все остальные модули коэффициен- |
|||||
|
|
|
|
1 и для |
||||||
тов ДПФ равняются нулю. Для q0 |
4 имеет место |
с0(4) |
||||||||
k 4 выполнятся условие |
|
с0(k) |
|
0. |
|
|
|
|||
|
|
|
|
|
||||||
Рис. 4.2.2. График для вычисления нормированных коэффициентов ДПФ c0 (k)
В том случае, когда комплексная синусоида укладывается почти целое число периодов на интервале наблюдения, примерно равное q0 , амплитудный спектр ДПФ сосредоточен в области значений k,
121
близких к q0; вне этой области амплитудный спектр ДПФ является
почти нулевым. Для случаев, когда комплексная синусоида не укладывается целое число периодов на интервале наблюдения, амплитудный спектр ДПФ является «размазанным».
Рассмотрим вид зависимости амплитудного спектра ДПФ – мо-
|
|
|||||||
дулей коэффициентов |
с(k) |
от дискретного номера k для комплекс- |
||||||
ной |
экспоненциальной |
функции. |
Для |
(4.2.1) зададим А 1, |
||||
f |
29,4 Гц, |
0,5, |
|
N |
512, |
T |
0,01 c; для данной функции |
|
параметр q NTf |
150,25, |
q0 |
150, |
q |
0,25. На рис. 4.2.3 изо- |
|||
бражѐн график амплитудного спектра ДПФ в логарифмическом
|
, k |
0, 1,..., N |
1. Шаг дискретности по частоте |
||
масштабе L |
c(k) |
||||
спектра составляет |
величину |
f 1/NT |
0,1953 Гц. Значениям |
||
L c(k) могут быть поставлены в соответствие дискретные частоты
fk |
f k [Гц], k 0, 1,..., N 1, которые изменяются в диапазоне |
0 fk |
fN 1. |
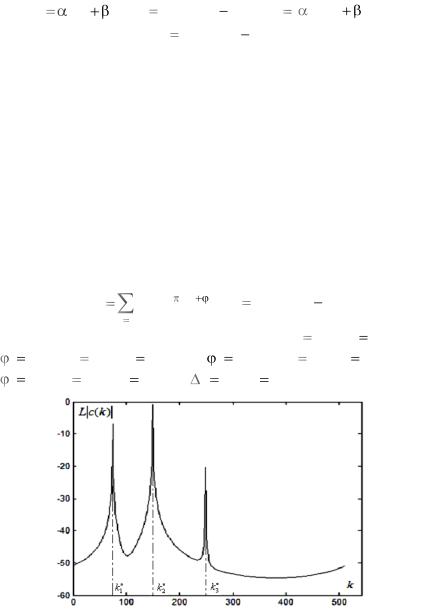
Из рис. 4.2.3 следует, что график L c(k) содержит резкий спектральный максимум в области k q0 : в указанной области со-
средоточены основные значения амплитудного спектра, вне области значения амплитудного спектра пренебрежимо малы. На основе графика амплитудного спектра может быть произведена оценка
Рис. 4.2.3. Амплитудный спектр ДПФ комплексной экспоненциальной функции в логарифмическом масштабе
122

параметров комплексной экспоненциальной функции. По значению номера k , соответствующего спектральному максимуму на графи-
ке рис. 4.2.3,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
k |
arg{ min |
L |
c(k) |
} |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
0 k |
N 1 |
q, |
оценивается частота f и |
||||||||||||||
и в предположении малого значения |
||||||||||||||||||||||||||
амплитуда |
A |
исходной |
экспоненциальной |
функции. В |
данном |
|||||||||||||||||||||
случае |
k |
150 |
и можно |
|
считать, |
что |
с |
некоторой |
погреш- |
|||||||||||||||||
ностью |
f |
fk |
29,295 Гц и |
А |
|
с(k ) |
|
, |
L |
|
c(k ) |
|
1,5 Дб, |
|||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
с(k ) |
|
10 1,5/20 |
|
0,8411 . Максимальная погрешность оценки час- |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
тоты составляет величину |
|
f |
f / 2 |
0,0977 Гц. Максимальная |
||||||||||||||||||||||
погрешность амплитуды определяется формулой |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
A |
|
|
A |
|
1 |
sin |
/ 2 |
, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2N |
|
|
|
|
|
|
|
|
|
|
||||
и при |
N |
512 |
принимает |
значение |
|
|
A |
0,38. Разумеется, при |
||||||||||||||||||
q0 величины данных погрешностей стремятся к нулю.
Сиспользованием (4.2.4) можно заключить, что оценка начальной фазы
(k ) |
(q k) |
N 1 |
, |
|
|
|
|||
|
|
N |
|
|
и для случая q 0 близка к значению начальной фазы |
. |
|||
4.2.2. Элементарные свойства ДПФ
Рассмотрим некоторые простейшие свойства ДПФ, которые будут использованы в дальнейшем.
1. ДПФ является линейной операцией. Пусть дискретная последо-
вательность |
z(i) |
образуется как |
сумма последовательностей |
x(i), y(i) , i |
0, 1,..., N 1, с весами |
, и известны ДПФ этих по- |
|
следовательностей: |
cх (k), cy (k), |
k 0, 1,..., N 1. Тогда ДПФ |
|
сz (k) для последовательности z(i) представляет собой взвешенную сумму ДПФ cx (k), cy (k) :
123
z(i) |
x(i) y(i), i 0, 1,..., N 1, сz (k) |
cx (k) cy (k), |
k0, 1,..., N 1.
2.Благодаря особенностям ДПФ от комплексной экспоненциальной функции и свойству линейности с использованием ДПФ оказывается удобным производить анализ многочастотных сигналов. Пусть наблюдаемый сигнал представляет собой сумму нескольких синусоид с частотами, которые различаются в достаточной степени. Тогда амплитудный спектр ДПФ такого сигнала содержит набор спектральных максимумов: количество спектральных максимумов равняется числу частотных составляющих в сигнале, а частотные координаты и высоты спектральных максимумов определяются частотами и амплитудами составляющих. На основе амплитудного спектра ДПФ возможно приближѐнное решение достаточно сложной задачи оценивания параметров многочастотных сигналов.
Проведѐм вычисления ДПФ для суммы трѐх комплексных экспоненциальных функций с различными частотами
|
|
|
3 |
A e j(2 fsTi |
s ) , |
|
|
|
|
|
|
|
|
|
|
y(i) |
i 0, 1,..., N 1. |
|
(4.2.5) |
||||||
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
s 1 |
|
|
|
|
|
|
|
|
|
Для |
(4.2.5) |
примем |
значения |
параметров |
A |
0,5; |
f |
14,6 |
Гц; |
|||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
1,0; |
A2 |
1,0; f2 |
29,4 Гц; |
1 |
0,5 |
и |
A3 |
1,5; |
f1 |
48,76 |
Гц; |
1 |
1,5; |
N |
512; T |
0,01 c; f |
1/ NT |
0,1953 Гц. На рис. 4.2.4 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
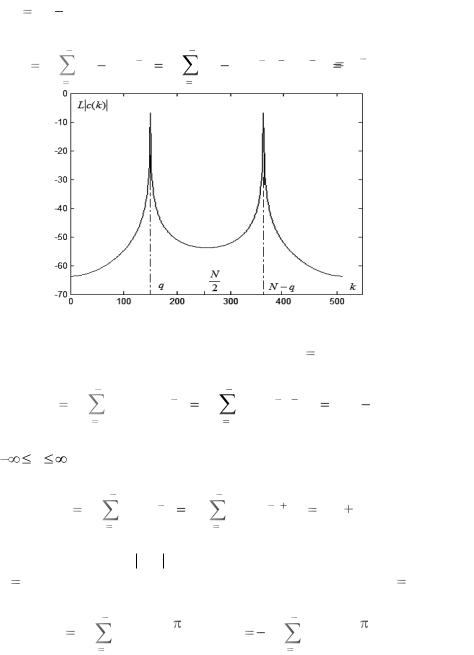
Рис. 4.2.4. Амплитудный спектр ДПФ для трехчастотной комплексной функции
124

изображѐн логарифмический амплитудный спектр ДПФ трѐхчастотной комплексной функции (4.2.5). Видно наличие в нѐм трѐх спек-
тральных максимумов, соответствующих частотам |
f1, f2 |
и |
f3. |
|||||||||||||||
|
|
По виду |
графика |
L |
c(k) |
рис. 4.2.4 определяются |
положения |
|||||||||||
спектральных максимумов k1 |
74, |
k2 |
150, k3 249, на основе ко- |
|||||||||||||||
торых |
оцениваются |
|
соответствующие |
частоты |
fs |
fks ; |
||||||||||||
s = 1, 2, 3; |
f1 0,1953 74 |
14,45 Гц; |
f21 |
0,1953 150 |
29,29 Гц; |
|||||||||||||
f3 |
0,1953 249 |
48,63 Гц |
и |
логарифмические |
амплитуды |
|||||||||||||
L |
c(k1 ) |
7 Дб; |
L |
c(k2 ) |
|
|
1 Дб; |
L |
c(k3 ) |
20 Дб. После пере- |
||||||||
счѐта |
получаются |
оценки амплитуд |
А |
10 7/20 |
0,447; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
А |
10 |
1/20 |
0,891; А 10 20/20 |
0,1. |
В силу различия в доста- |
|||||||||||||
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
точной степени частот |
f1 |
f3 амплитудный спектр ДПФ для подоб- |
||||||||||||||||
ной трехчастотной функции может представляться в виде суммы амплитудных спектров ДПФ составляющих.
3. Воспользовавшись свойством линейности можно вычислить ДПФ действительной косинусоидальной (синусоидальной) функции y(i) cos2 fTi, i 0, 1,..., N 1. Приведѐм известные соотноше-
ния |
|
|
|
|
|
|
|
|
Wqi e j2 fTi |
cos2 fTi |
jsin2 fTi, |
q |
NTf , W Ni |
1, |
|||
cos2 |
fTi |
W qi |
W qi |
W qi |
W(N q)i |
. |
(4.2.6) |
|
|
2 |
|
|
2 |
||||
|
|
|
|
|
|
|
||
Из (4.2.6) следует, что ДПФ для функции |
y(i) cos2 fTi представ- |
|||||||
ляет собой сумму ДПФ для комплексных экспоненциальных функций с параметрами q и (N q). На рис. 4.2.5 изображѐн логарифми-
ческий амплитудный ДПФ-спектр для косинусоидальной функции y(i) cos2 fTi.
Анализируя график рис. 4.2.5 можно сделать вывод, что ДПФ косинусоидальной функции состоит из двух составляющих, симметричных относительно точки N/2.
4. Рассмотрим влияние сдвигов при вычислении ДПФ. Пусть задана последовательность y(i), i 0, 1,..., N 1. Продолжим эту по-
следовательность с периодом N. Осуществим сдвиг данной последовательности на i0 единиц, образуем новую последовательность
125
z(i) y(i |
i0 ). Вычислим коэффициенты ДПФ для последователь- |
||||||||
ности z(i), |
с учѐтом периодичности |
|
|
|
|
||||
|
1 N 1 |
1 N 1 |
|
ki0 c |
|
|
|||
с (k) |
|
|
y(i i )W ki |
|
y(i i )W k(i i0)W ki0 |
W |
у |
(k). |
|
|
|
|
|||||||
z |
N i |
0 |
0 |
|
|
|
|||
|
0 |
N i 0 |
|
|
|
|
|||
Рис. 4.2.5. Амплитудный спектр ДПФ для косинусоидальной функции
Справедливо и обратное утверждение. Если z(i) |
W k0i y(i), |
тогда c |
|||||||||||
помощью почти аналогичных выкладок получим |
|
|
|
|
|||||||||
|
1 N 1 |
1 |
|
N 1 |
|
|
|
|
|||||
с (k) |
|
|
|
Wk0i y(i)W ki |
|
|
|
|
y(i)W (k k0 )i |
c |
y |
(k k ). |
|
|
|
|
|
|
|
||||||||
z |
N i |
|
|
|
N i 0 |
|
|
0 |
|||||
|
0 |
|
|
|
|
|
|||||||
5. Коэффициенты ДПФ |
c(k) |
можно рассматривать для |
|||||||||||
k . Тогда можно утверждать, что c(k) периодичны по k с |
|||||||||||||
периодом N. В самом деле |
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
N 1 |
1 N 1 |
|
|
|
|
|||||
c(k) |
|
|
|
y(i)W ki |
|
|
|
|
y(i)W( k N)i |
c(k N). |
|
||
|
|
|
|
|
|
|
|
||||||
|
|
N i 0 |
N i |
0 |
|
|
|
|
|||||
6. Установим для действительных последовательностей модулей коэффициентов ДПФ с(k) свойство симметрии относительно точки
k N/2. Положив мнимую составляющую наблюдений y2 (i) 0, представим выражения для действительной и мнимой частей ДПФ:
|
1 N 1 |
|
2 |
|
1 |
N 1 |
2 |
|
|
c (k) |
|
|
y (i)cos |
|
ki, c (k) |
|
y (i)sin |
|
ki. |
|
|
|
|
|
|||||
1 |
N i 0 |
1 |
|
2 |
|
1 |
|
|
|
|
|
N |
|
N i 0 |
N |
|
|||
|
|
|
|
|
126 |
|
|
|
|
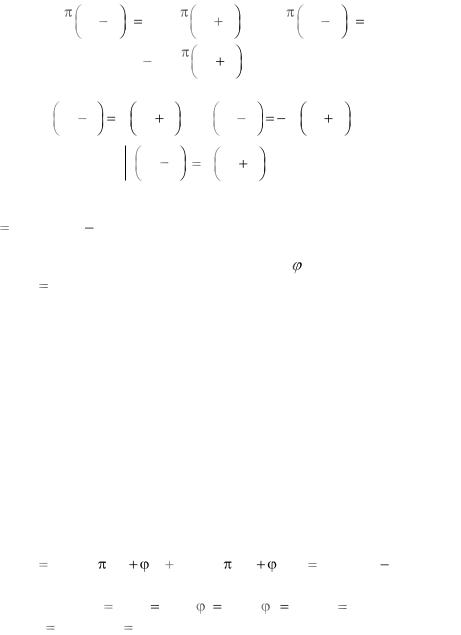
Запишем очевидные равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
cos |
2 |
|
N |
k i |
|
cos |
2 |
|
|
|
N |
|
|
k |
i, |
sin |
2 |
|
N |
|
k i |
|||
N |
2 |
|
N |
2 |
|
N |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
= sin |
2 |
|
|
|
N |
|
k |
i, |
|
|
|
|
|
|
|
||||
|
|
|
|
|
N |
2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
из которых следует свойство симметрии |
|
|
|
|
|
|
|
|
||||||||||||||||
с1 |
N |
k |
c1 |
N |
k , |
|
|
с2 |
|
N |
k |
|
c2 |
|
N |
k , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
2 |
|
|
|
2 |
|
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
c |
N |
k |
|
c |
N |
k |
|
. |
|
|
|
||||||||
2 |
2 |
||||||||
|
|
|
|
|
|
|
При анализе действительных сигналов вполне оправданно рас-
смотрение |
амплитудных |
спектров |
ДПФ |
для |
точек |
k 0, 1,..., |
N/2 1. |
|
|
|
|
Аналогичным образом может быть установлено свойство центральной симметрии для фазовых углов ДПФ (k) относительно точки k N/2.
4.2.3. Разрешающая способность ДПФ
Амплитудный спектр ДПФ для многочастотных сигналов в общем случае, с учѐтом некоторых упрощающих предположений, состоит из набора спектральных максимумов. С помощью оценивания параметров амплитудного спектра ДПФ возможно решение многих задач анализа сложных колебательных сигналов.
Однако в ряде случаев проведение анализа сигналов на основе амплитудного спектра ДПФ сопряжено с рядом проблем. Эффективность анализа сигналов зависит, в частности, от разрешающей способности ДПФ-возможности различения на амплитудном спектре ДПФ спектральных максимумов составляющих для многочастотных сигналов с близкими частотами.
Рассмотрим пример двухчастотного действительного сигнала
y(i) |
A1 cos(2 |
f1Ti |
1) |
A2 cos(2 |
f2Ti |
|
2), i |
0, 1,..., N |
1. |
|
|
|
|
|
(4.2.7) |
|
|
|
|
|
|
с параметрами A |
1; |
A |
1,5; |
1 |
0,5; |
2 |
0,8; |
Т 0,01. |
Для |
|
|
1 |
|
2 |
|
|
|
|
|
||
(4.2.7) f1 |
20 Гц, |
f2 |
20,06 Гц – частоты составляющих. Для рас- |
|||||||
|
|
|
|
|
127 |
|
|
|
|
|
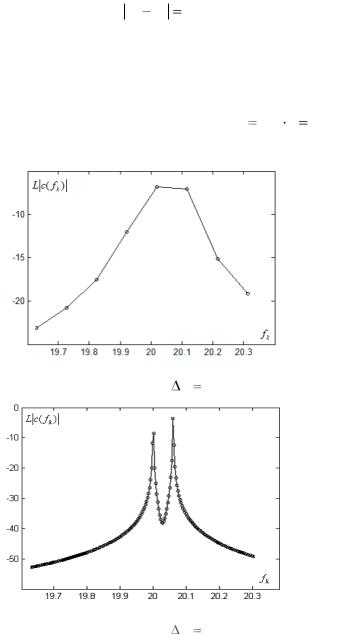
сматриваемого двухчастотного сигнала разность частот для составляющих принимает значение f1 f2 0,06 Гц. Для (4.2.7) вычислим ДПФ при различных вариантов величин интервалов наблюдений. Вид амплитудного спектра зависит от разности частот f1, f2 и
шага дискретности спектра по частоте и особенностей аппаратной функции.
На рис. 4.2.6а изображены результаты вычисления логарифмиче-
|
|
|
|
ского амплитудного спектра L |
c( fk ) |
для |
N1 512 2 1024 и |
длины интервала наблюдения, составляющей |
10,24 c . Кружками |
||
Рис. 4.2.6а. Логарифмический амплитудный спектр ДПФ двухчастотного сигнала, f1 0,0976 Гц
Рис. 4.2.6б. Логарифмический амплитудный спектр ДПФ двухчастотного сигнала, f2 0,0031 Гц
128

|
|
|
|
|
|
|
|
|
|
|
|
отмечены |
восемь |
значений |
L |
c( fk ) |
с |
|
шагом дискретности |
||||
f1 1/ N1T |
0,0976 Гц,для k |
201 |
208, |
|
соответствующих час- |
||||||
тотам 19,62 20,30 Гц . |
|
|
|
|
|
|
|
||||
В данном случае |
|
f1 f2 |
|
f1, ( |
|
f1 |
f2 |
|
/ f1 0,62 – расстоя- |
||
|
|
|
|
||||||||
ние по частоте между составляющими сигнала меньше шага дискретности спектра. В силу указанных неравенств на данном амплитудном спектре принципиально не могут быть видны раздельно составляющие сигнала – частотные составляющие в сигнале не разрешимы на основе ДПФ с f1 
Для повышения разрешающей способности ДПФ производится увеличение временного интервала наблюдения. На рис. 4.2.6б изображены результаты вычисления логарифмического амплитудного
спектра L c( fk ) для N2 512 64 32768; длина временного ин- |
тервала наблюдения и дискретность спектра по частоте составляют
327,68 c и |
f2 |
|
1/ N2T |
0,0031 Гц. |
Поскольку в данном случае |
||
f1 f2 |
|
f2 |
( |
f1 f2 |
/ |
f2 19,35), |
то в силу указанных нера- |
венств амплитудный спектр ДПФ состоит из двух отчѐтливо видимых раздельно спектральных максимумов – две частотные составляющие в сигнале разрешимы на основе ДПФ с f2 0,0031 Гц .
Разрешающая способность ДПФ определяется величиной f 1/ NT, которая совпадает с шагом дискретности по частоте ам-
плитудного спектра. Если обратиться к (4.2.7) и учесть свойства аппаратной функции, то спектр первой составляющей сосредоточен
около частоты |
f1 и для частот fk , удовлетворяющих неравенству |
|||
|
fk f1 |
|
10 f , |
спектр первой составляющей становится сущест- |
|
|
|||
венно малым. Аналогично, для второй составляющей спектр сосредоточен около частоты f2 и для частот дискретных fk , удовлетво-
ряющих неравенству fk f2 10 f , спектр второй составляющей
становится существенно малым.
Общее правило приближѐнного определения разрешимости составляющих сигнала с близкими частотами f1, f2 на основе спектра ДПФ с учѐтом значения шага дискретности по частоте f может
быть сформулировано следующим образом. Если для частот составляющих в сигнале выполняется неравенство
129

f1 f2 (5 10) f ,
то составляющие не разрешимы на основе ДПФ. Если для частот составляющих в сигнале выполняется противоположное неравенство f1 f2 (5 10) f ,
то составляющие разрешимы на основе ДПФ.
4.3. Функция спектральной плотности мощности сигналов
4.3.1. Теорема Парсеваля
Существуют два подхода, которые обычно применяются при исследовании свойств и характеристик сигналов. Первый подход базируется на обычных представлених во временной области, при которых сигналы у(t) рассматриваются как функции времени для
t . Второй подход связан с представлениями в частотной области, при которых сигналы или образы сигналов в виде преобразований Фурье C( j ),рассматриваются как функции частоты для
. Указанные подходы, являющиеся равноправными и двойственными, базируются на возможности реализации прямого и обратного преобразований Фурье, взаимнооднозначно связывающих временные и частотные представления сигналов. Теорема Парсеваля позволяет устанавливать величину полной энергии комплексных сигналов с помощью интегрирования либо во временной, либо в частотной областях.
Основываясь на разд. 2.2, обратимся к выражению для вычисления энергии E комплексного сигнала у(t) во временной области в
виде интеграла
Еy*(t) y(t)dt. (4.3.1)
Используем обратное и комплексно-сопряжѐнное обратное преобразования Фурье, сформируем выражения для сигналов y(t) и y*(t) :
y(t) |
C( j )e j t d , y*(t) |
C*( j )e j t d . |
(4.3.2) |
Подставим выражения (4.3.2) в интеграл (4.3.1) и переставим порядки интегрирования
130
