
getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie
.pdf
E |
|
C( j )e j t d |
|
C*( j |
1 |
)e |
|
j 1t d |
1 |
dt, (4.3.3) |
||
|
|
|
|
|
|
|
|
|
|
|
||
|
E |
C( j )d |
C( j |
1 |
)d |
1 |
|
e j( |
1)t dt. |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Последний |
интеграл будет |
представлять |
собой |
-функцию из |
||||||||
разд. 2.5.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e j( |
1)t d 2 ( |
|
|
1 |
). |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Нетрудно видеть, что справедливо равенство, из которого величина полной энергии сигнала может быть вычислена на основе интегрирования в частотной области:
E C( j )d C*( j 1)d 12 ( 1) 2 С*( j )С( j )d ., (4.3.4)
Е y*(t)y(t)dt 2 С*( j )С( j )d . (4.3.5)
Равенство (4.3.5) представляет собой формулировку теоремы Парсеваля и позволяет вычислять полную энергию сигнала как во временной, так и в частотной областях.
Прямое и обратное ДПФ может служить дискретным аналогом прямого и обратного непрерывного преобразования Фурье. Разберѐм вывод дискретного аналога теоремы Парсеваля.
Запишем обратное и сопряжѐнное обратное ДПФ для дискретных
значений сигнала y(i), |
i 0, 1,..., N 1: |
|
N 1 |
N 1 |
|
y(i) |
c(k)Wki , y*(i) |
c*(k)W ki . |
k 0 |
k |
0 |
Образуем произведения y*(i)y(i), просуммируем их по i, изменим порядок суммирования и получим
N 1 |
|
N 1 |
N 1 |
|
E |
y*(i)y(i) |
|
c*(k)W |
|
i |
0 |
|
i 0 |
k 0 |
|
N 1 |
N 1 |
N 1 |
|
|
|
c*(k) |
c(s) |
W(s k)i |
|
k 0 |
s 0 |
i |
0 |
|
|
|
|
131 |
|
N 1 |
ki |
c(k)W si |
s 0
N 1
N c*(k)c(k). (4.3.6)
k 0

На основе (4.3.6) сформируем выражение, которое является дискретным аналогом теоремы Парсеваля:
N 1 |
N 1 |
|
|
E |
y*(i)y(i) N |
c*(k)c(k). |
(4.3.7) |
i 0 |
k |
0 |
|
4.3.2. Определение функции спектральной плотности мощности сигналов
Определение функции спектральной плотности мощности (СПМ) сигналов связано с аналогией из электротехники – вычислении мощности, выделяемой на активном сопротивлении
(см. разд. 2.2).
Применим теорему Парсеваля (4.3.5) для нахождения величины энергии сигнала y(t), приходящейся на узкий интервал частот
( , |
d ) : |
E(y, ,d ) 2 C*y ( j )Cy ( j )d .
Для функции спектральной плотности мощности для стационарного эргодического сигнала Pyy ( ) в непрерывном случае сформи-
руем отношение части мощности сигнала в частотном диапазоне ( , d ) к величине d . Для этого рассмотрим прямое и ком-
плексно-сопряжѐнное прямое преобразование Фурье для сигнала
y(t) на интервале времени T0 / 2 |
t |
T0 / 2, которые представля- |
|||||
ются интегралами |
|
|
|
|
|
|
|
|
|
|
|
1 |
T0 /2 |
|
|
С |
|
( j ,T ) |
|
y(t)e j t dt, |
|||
y |
|
|
|||||
|
|
||||||
|
|
0 |
2 |
|
|
|
|
|
|
|
|
T0 |
/2 |
|
|
|
|
|
|
|
(4.3.8) |
||
|
|
|
|
|
T0 /2 |
||
|
|
|
|
1 |
|
||
С* ( j ,T ) |
|
y*(t)e j t dt. |
|||||
|
|
||||||
|
|
||||||
|
y |
|
0 |
2 |
|
|
|
|
|
|
|
T0 |
/2 |
|
|
|
|
|
|
|
|
||
Энергия сигнала y(t) |
длительностью |
T0 в частотном диапазоне |
|||||
( , d ) может быть найдена на основе интегралов (4.3.8)
E(у, , d , T0) 2 C*y ( j , T0)Cy ( j , T0)d .
Функция СПМ Pyy ( ) для рассматриваемого стационарного эрго-
дического сигнала запишется в виде предела, в предположении, что этот предел существует:
132

|
1 |
E( y, ,d ,T ) |
|
2 |
C* ( j ,T )C |
|
( j ,T )d |
||
|
|
|
|
y |
|||||
|
0 |
|
|
y |
0 |
0 |
|
||
Pyy ( ) lim |
T0 |
lim |
T0 |
|
|
|
, |
||
|
d |
|
|
d |
|
|
|||
T0 |
|
T0 |
|
|
|
|
|
||
P ( ) lim |
2 |
C* ( j |
,T )C ( j |
,T ). |
(4.3.9) |
|
|
||||||
yy |
|
|
y |
0 y |
0 |
|
|
T0 |
Т0 |
|
|
|
|
Функция |
Pyy ( ) в общем случае определена во всѐм частотном |
диапазоне |
и является положительной Pyy ( ) 0. |
Рассмотрим обобщение определения функции СПМ сигналов (4.3.9) для дискретного случая. Пусть задаѐтся набор дискретных значений сигнала y(i) y(Ti), i 0, 1,..., N 1, T – интервал дис-
кретизации. Интегралы Фурье из (4.3.8) могут быть заменены дискретными суммами, которые являются фактически оценками ука-
занных интегралов для |
|
заданной |
|
частоты |
k |
2 k/(NT), |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0, 1,..., N 1 и и с учѐтом t |
Ti, |
T0 |
TN : |
|
|
||||||||
|
1 |
|
N 1 |
|
|
|
j |
2 |
kTi 1 |
|
|
||
Cy ( j k , TN) |
|
T |
y(i)e |
|
NT |
TNcу |
(k), |
||||||
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
2 |
||||||||
|
|
i |
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Cy* ( j |
k , TN) |
|
1 |
TNc*у (k). . |
|
|
|||||||
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Нетрудно видеть, что оценки интегралов Фурье сформированы в виде ДПФ. Поэтому Pyy ( k ) – оценка функции СПМ дискретизо-
ванного сигнала для фиксированных частот k – может быть вычислена через коэффициенты ДПФ:
P ( |
|
) |
2 |
|
|
C * ( j |
|
,TN)C |
( j |
|
,TN) |
2 |
1 |
TNc*(k) |
1 |
TNc(k), |
|||||
k |
|
|
|
|
k |
k |
|
|
|
|
|||||||||||
yy |
|
|
TN |
|
y |
y |
|
|
TN 2 |
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
P ( |
k |
) |
P c*(k)c(k), k |
|
0, 1,..., N |
1, |
P |
|
TN . |
(4.3.10) |
||||||||
|
|
|
yy |
|
0 |
|
|
|
|
|
|
|
|
0 |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3.3. Функции временных окон |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Погрешности |
предложенной |
оценки |
(4.3.10) |
функции СПМ |
|||||||||||||||||
Pyy ( k ) стационарного эргодического сигнала обусловливаются, в
основном, двумя факторами: заменой непрерывного сигнала на дискретный и конечностью интервала наблюдения. Точность оце-
133

нивания функции СПМ будет повышаться при уменьшении интервала дискретизации и увеличении длительности времени наблюдения.
Проанализируем возможность повышения точности оценивания функции СПМ для фрагмента сигнала, определѐнного на некотором конечном интервале времени. Рассмотрим погрешность, которая вносится конечностью интервала интегрирования при вычислении преобразований Фурье. Для сигнала y(t) запишем преобра-
зование Фурье на бесконечном и конечном симметричном времен-
ном интервале |
Т0 /2 t |
T0 /2: |
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
1 |
T0 /2 |
|
|
||
C( j ) |
|
y(t)e |
j t dt, C ( j ,T ) |
|
y(t)e |
j t dt. |
|
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
2 |
|
|
0 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
T0 |
/2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Очевидно, |
|
что |
С( j |
) С0 ( j , T0 ) |
и |
|
С( j , T0 ) |
С( j |
) |
||
С0 ( j , T0 ) – погрешность преобразования Фурье сигнала |
y(t), |
||||||||||
вызванная |
конечным |
интервалом интегрирования; |
С2(T ) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
С( j , T0)
 – мера погрешности. Преобразование Фурье на ко-
– мера погрешности. Преобразование Фурье на ко-
нечном интервале может замениться вычислением интеграла на бесконечном интервале, если ввести функцию прямоугольного
временного окна w0 (t, T0 ) |
1 для |
Т0 /2 t T0 /2 и w0(t, T0 ) 0 |
||
для t T0 /2, t |
T0 /2: |
|
|
|
С ( j , T ) |
1 |
w (t, T )y(t)e j t dt. |
||
|
||||
|
||||
0 |
0 |
2 |
0 |
0 |
|
|
|
|
|
При стремлении величины временного интервала интегрирования T0 к бесконечности имеет место очевидный предел
lim |
С2 (Т ) 0. |
T0 |
0 |
|
Согласно сделанным ранее рассмотрениям в разд. 2.5.3, преобразование Фурье от произведений функций вычисляется как интегральная свѐртка преобразований Фурье сомножителей:
C0 ( j , T0 ) |
W0 ( j( |
1), T0 )С( j 1)d 1, |
(4.3.11) |
где W0 ( j , T0 ) – преобразование Фурье функции прямоугольного временного окна w0 (t, T0 ). Приведѐм выражение преобразования
134
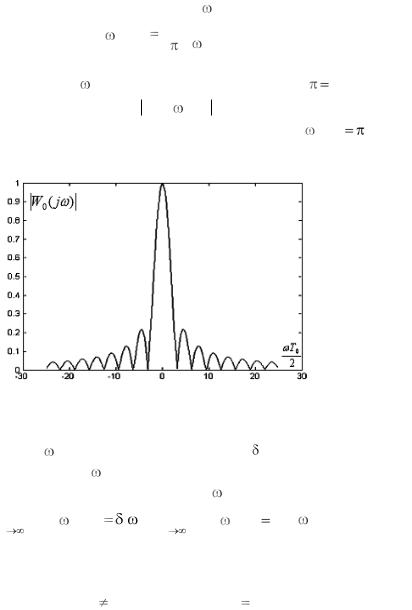
Фурье, которое в силу чѐтности w0 (t, T0 ) является действительной функцией
|
|
|
T |
|
sin |
T0 |
|
|||
|
|
|
|
2 |
|
|
||||
|
W ( j , T ) |
0 |
|
|
|
. |
(4.3.12) |
|||
|
|
|
|
|
||||||
0 |
0 |
2 |
|
|
|
T0 |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
для частного значения T0 /2 |
1 изо- |
||||||||
График модуля |
W0( j , T0) |
|||||||||
бражѐн на рис. 4.3.1. Функция W0( j , T0) состоит из главного лепестка, ширина которого определяется из соотношения T0 /2 , и системы медленно спадающих по амплитуде боковых лепестков.
Рис. 4.3.1. Модуль преобразования Фурье функции прямоугольного окна
При увеличении Т0 для прямоугольного окна его преобразование Фурье W0 ( j , T0 ) вида (4.3.12) стремится к -функции; преобразование Фурье С0 ( j , T0 ), в соответствии с формулой инте-
гральной свѐртки (4.3.11), стремится к С( j |
) |
|
lim W0 ( j , T0 ) |
( ), lim С0 ( j |
, T0 ) С( j ). |
T0 |
T0 |
|
Возможность снижения погрешности оценивания функции СПМ, возникающей из-за конечности временного интервала, может реализовываться на основе выбора подходящей функции временного окна w(t, T0 ) w0 (t, T0 ), w(t, T0 ) 0 вне интервала
135

Т0 /2 t T0 /2. Умножение сигнала |
y(t) на функцию временно- |
||||||
го окна w(t, T0 ) на интервале |
Т0 /2 |
t T0 /2, |
y(t, T0 ) |
y(t)w(t, T0) |
|||
описывается свѐрткой в частотной области |
|
|
|||||
|
|
|
|
|
|
|
|
C( j ,T0 ) |
W( j( |
1),T0 )С( j |
1)d 1. |
(4.3.13) |
|||
Пусть функция временного окна w(t, T0 ) будет устроена таким образом, что еѐ преобразование Фурье W( j , T0 ) оказывается близким к -функции; W( j , T0 ) должна будет иметь высокий и
узкий главный лепесток и систему малых боковых лепестков. Тогда имеются основания полагать, что в результате интегрирования
свѐртки (4.3.13) преобразование Фурье C( j ) будет близко к C( j ). Последнее соответствует реализации приближѐнного равенства C( j ) C( j ), что эквивалентно снижению погрешности
при оценивании функции СПМ. |
|
Перейдѐм к дискретным значениям сигнала y(i), 0 i |
, и |
функции временного окна w(i), определѐнной на конечном интервале наблюдения i 0, 1,..., N. После умножения наблюдений на
функцию временного окна получим последовательность y(i)  w(i)y(i), i 0, 1,..., N..
w(i)y(i), i 0, 1,..., N..
Вычислим z-преобразование для последовательности y(i), ко-
торое может быть найдено на основе z-преобразований последовательностей y(i) и w(i) :
|
|
N |
|
|
Y(z) |
y(i)z i , W(z) |
w(i)z i , Z{y(i)} Y (z). |
||
|
i 0 |
i 0 |
||
Воспользуемся материалами разд. 2.6 и формулой (2.6.3), сделаем подстановку z e j T и запишем выражение для частотной функции Y (e j T ) на основе свѐртки частотных функций окна W(e j T ) и сигнала Y(e j T ) :
|
|
|
T |
2 /T |
Y |
(e j T ) |
|
W(e j 1T )Y(e j( 1)T )d . |
|
|
||||
|
|
|
2 |
1 |
|
|
|
0 |
|
|
|
|
|
|
Очевидно, для того, чтобы частотная функция Y (e j T ) была близка к частотной функции Y(e j T ), необходимо, чтобы частотная функ-
136
ция окна W(e j T ) была близка к -функции – имела бы высокий
главный лепесток в узком частотном диапазоне и незначительные боковые лепестки.
Рассмотрим некоторые варианты оконных функций. Примем для удобств выкладок временной интервал симметричным, положим N чѐтным и определим окно в точках N/2 i N/2 (в N + 1
точках).
Функция прямоугольного временного окна w0 (i) является ба-
зисной для настоящего рассмотрения и представляется соотношениями
w0 (i) 1 для N/2 i N/2 , w0 (i) 0 для i N/2, i N/2 .
Вычислим в соответствии с (2.6.3) частотную функцию для прямоугольного окна
N/2 |
|
e j TN /2 |
e |
j |
TN /2e j T |
W (e j T ) |
e j Ti |
|
|
|
|
0 |
|
1 |
e |
j |
T |
i N/2 |
|
||||
|
|
|
|
|
e j T (N |
1)/2 |
e j |
T /2 |
e e
j |
T (N 1)/2 |
sin( T(N 1)/2) . |
|
j |
T /2 |
(4.3.14) |
|
sin( T /2) |
|
||
|
|
|
В силу чѐтности w0 (i) функция W0(e j T ) является действительной.
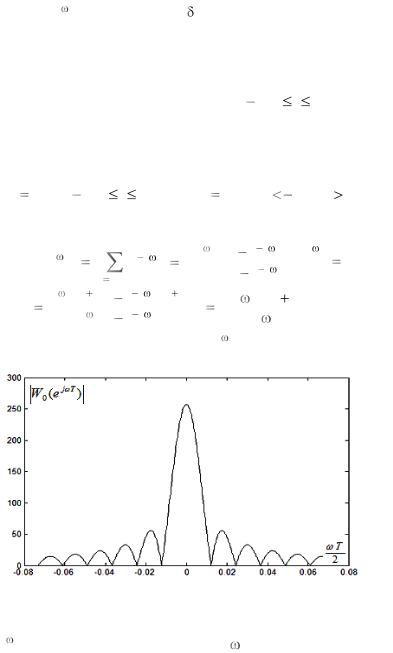
Рис. 4.3.2. Модуль частотной функции прямоугольного окна
|
На |
рис. 4.3.2 изображѐн график модуля частотной функции |
||
|
W (e j |
T ) |
|
в зависимости от переменой Т /2, для примера взято |
|
|
|||
|
0 |
|
|
|
|
|
137 |
||
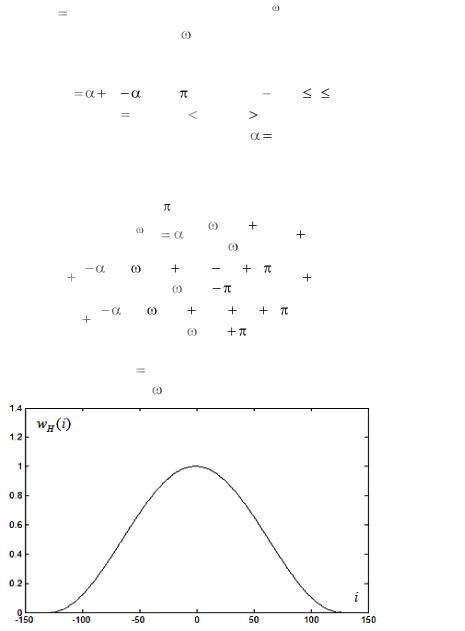
значение N 256. |
Частотная функция W (e j |
T ) является анало- |
||||
|
|
|
0 |
|
|
|
гом преобразования Фурье W0 ( j , T0 ). |
|
|
|
|||
Функции временных окон Хэннинга wH (i) |
и Хэмминга wHm (i) |
|||||
отличаются параметрами и описываются формулой |
|
|||||
wH (i) |
(1 |
)cos(2 |
i / N) для |
N / 2 |
i N / 2, |
|
wN (i) |
0 для i |
N / 2, i |
N / 2, |
(4.3.15) |
||
для окна Хэннинга выбирается значение |
|
0,5 , |
для окна Хэм- |
|||
минга – 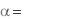 Вычисления частотных функций окон Хэннинга и Хэмминга
Вычисления частотных функций окон Хэннинга и Хэмминга
производятся на основе частотных функций прямоугольного окна,
сдвинутых вправо и влево на : |
|
|
|
|
|
||||||
|
|
W (e j |
T ) |
sin( T(N 1) / 2) |
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
H |
|
|
sin( |
T / 2) |
|
||
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
sin( |
T(N |
1) / 2 (N 1) |
/ N) |
(4.3.16) |
||||
|
2 |
|
|
|
sin( |
T / 2 |
/ N) |
|
|||
|
|
|
|
|
|||||||
1 |
|
|
sin( T(N |
1) / 2 |
(N |
1) / N) . |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
sin( |
T / 2 |
/ N) |
|
|||
На рис. 4.3.3а, 4.3.3б изображены функция временного окна
Хэннинга wH (i) для N |
256 и модуль еѐ частотной функции в |
зависимости от переменой |
Т /2. |
Рис. 4.3.3а. Функция временного окна Хэннинга
138
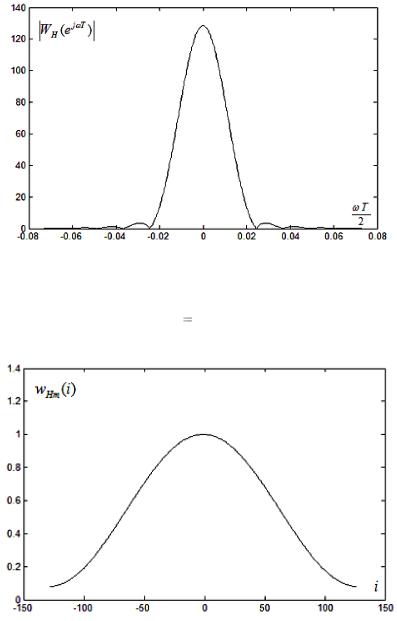
Рис. 4.3.3б. Модуль частотной функции окна Хэннинга
Рис. 4.3.4а, 4.3.4б содержат изображения функции временного окна Хэмминга wHm (i) для N 256 и модуля еѐ частотной функции.
Рис. 4.3.4а. Функция временного окна Хэмминга
139
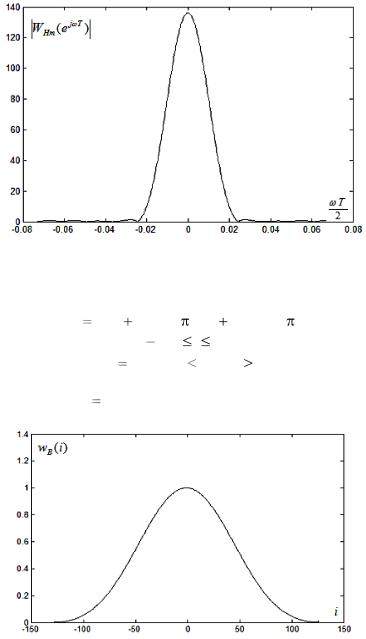
Рис. 4.3.4б. Модуль частотной функции окна Хэмминга
Функция временного окна Блэкмана |
wB (i) описывается весо- |
|||
вой функцией |
|
|
|
|
wB (i) 0,42 |
0,5сos2 i / Ni |
0,08cos4 i / N |
||
для |
N/2 i N/2 , |
(4.3.17) |
||
wB (i) |
0 |
для i N/2, |
i |
N/2 . |
На рис. 4.3.5а, 4.3.5б изображены функция временного окна Блэкмана wB (i) для N 256,и модуль частотной функции окна Блэкмана.
Рис. 4.3.5а. Функция временного окна Блэкмана
140
