Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белгородский университет кооперации, экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie / getmanov_v_g_cifrovaya_obrabotka_signalov_uchebnoe_posobie

.pdf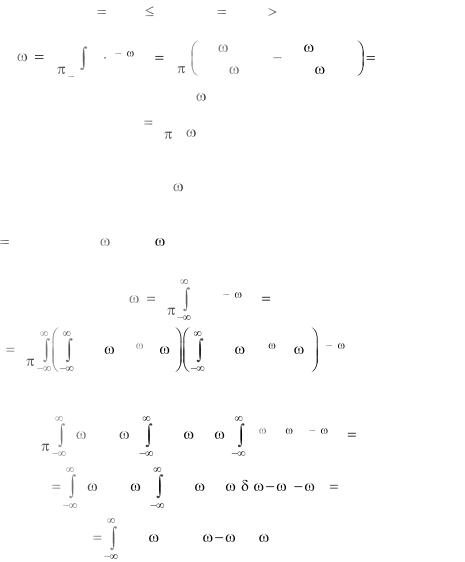

Скачиваний:

Добавлен:

18.03.2016

Размер:

6.41 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 248 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

6. Вычислим преобразование Фурье для симметричного единичного импульса:

		y(t) 1,			t	T0	,		y(t) 0,				t	T0		,
						T0								T0
						2								2
		T0 /2				2								2
	1	T0 /2					1				sin (T / 2)				sin (T / 2)
	1										sin (T / 2)				sin (T / 2)
C( j )			1 e	j t dt							0					0
C( j )	2		1 e	j t dt		2
	2	T0	/2			2
		T0	/2
								sin			T0
						T		sin		2
						0				2		.
												.
						2				T0

Ввиду симметричности рассматриваемого единичного импульса его преобразование Фурье C( j ) является действительной функ-

цией.

7. Найдѐм преобразование Фурье для произведения функций

y(t) x(t)z(t), Cx ( j

), Cz ( j

) – соответственно, преобразования

Фурье для x(t), z(t). Запишем интегралы

( j )

y(t)e j t dt

С ( j

)e j 1t d

C ( j

)e j

2t d

e j t dt.

Изменив порядок интегрирования, с учѐтом выражения интеграла Фурье для комплексной синусоиды получим

1	d C ( j		) C ( j		)d		e j	1te j	2te j t dt
		1		2		2
2	1 x		z

	d 1Cx ( j 1) Cz ( j 2 )d 2 (							1	2 )
		Cx ( j 1)Cz ( j(					1))d 1.

Преобразование Фурье от произведения функций равняется свѐртке преобразований Фурье сомножителей.

2.6. z-Преобразование дискретных последовательностей

Положим, что сформирована комплексная бесконечная после-

довательность y(Ti), i 0, 1,...,	и z – некоторое комплексное число.
Обозначим через Y(z) сумму
Y(z)	y(Тi)z i .	(2.6.1)
i	0

По определению, выражение Y(z) есть z-преобразование последовательности y(Ti), при условии существовании суммы (2.6.1).

Рассмотрим	некоторые		простейшие примеры				вычисления
z-преобразований. Для		единичной последовательности						вида
y(iT) 1, i 0,	y(Тi) 0,	i	0	z-преобразование Y(z)			имеет	сле-
дующий вид:
		Y(z)		1		.
		Y(z)			1 z 1	.

Для комплексной экспоненциальной последовательности y(iT)

e j Ti , i 0, y(Тi)	0, i 0 Y(z) представится в виде
	Y(z)	1	.
		1 e j T z 1
Поскольку (2.6.1)	является степенным рядом переменной z 1,

то целесообразно проанализировать вопрос о сходимости этого ряда. Область сходимости ряда (2.6.1) определяется известным условием абсолютной сходимости

y(Ti)z i		(2.6.2)
	.

i 0

Для того, чтобы найти область сходимости для ряда (2.6.1), заменим модуль произведения в (2.6.2) произведением модулей

	y(Ti)z i		y(Ti)	z i	.

i 0		i 0

Вынесем нулевое слагаемое за знак суммы:

	y(Ti)z i	y(T 0)		y(Ti)	z i	.

i 0			i 1

Представим сумму в виде

y(Ti)

z i

y(Ti)

1/i

z 1

i .

i 1

Обозначим верхний предел последовательности

R max y(Ti)1/i ,

Поскольку значение любого отсчѐта выполняется, если

Ri z i

i 1

что возможно только при R z 1 1.

i 1, 2, 3...

конечно, то условие (2.6.2)

На комплексной плоскости

область сходимости располагается вне круга радиусом R.

Для дискретной последовательности y(i)

i область сходимо-

сти Y(z)

определяется из условия сходимости

y(Ti)

z i

i z i

z 1

i 0

которое выполняется при

z 1

1, откуда получаем область схо-

димости

и радиус сходимости R

На основе определения (2.6.1) z-преобразованию последова-

тельности y(Ti) в форме Y(z)	может быть поставлена в соответст-
вие частотная функция с помощью подстановки z		e j T :
Y(e j T )	y(Тi)e j Ti .	(2.6.3)
	i 0

Формулу Y(e j T ) (2.6.3) можно интерпретировать как аналог пре-

образования Фурье для дискретного случая.

Очевидно, последовательность y(Ti) есть обратное z-преобра- зование для Y(z), которое может быть найдено из (2.6.1) с использованием теоремы Коши. Для этого сначала умножим обе части

равенства (2.6.1) на zk 1 и затем произведѐм интегрирование по замкнутому контуру обеих частей равенства. Если контур интегрирования лежит внутри области сходимости бесконечного ряда (2.6.1), то операцию суммирования и интегрирования можно поменять местами:

Y(z)zk 1dz	y(Ti) zk i 1dz.	(2.6.4)
i	0

Согласно теореме Коши, в случае если контур интегрирования охватывает начало координат, то имеет место равенство

zk	i 1dz 0	(2.6.5)
для всех k, за исключением k	i. Для k	i интеграл (2.6.5) равен

2 j. Применим теорему Коши к выражению (2.6.4), получаем тео-

рему об обратном z-преобразовании
y(Ti)	1	Y(z)zi 1dz.			(2.6.6)
y(Ti)	2 j	Y(z)zi 1dz.			(2.6.6)
	2 j
Рассмотрим степенную последовательность				y(Ti)	i. Тогда вид-
но, что
Y(z)		1	z	.
Y(z)	1	z 1	z	.
	1	z 1	z

Для того, чтобы убедиться в том, что y(Ti) есть обратное z-пре- образование от Y(z), применим (2.6.6) и выполним интегрирование вдоль окружности радиуса большего, чем . Запишем

	1		zi
y(Ti)				dz.	(2.6.7)
y(Ti)	2 j	z		dz.	(2.6.7)
	2 j	z

Интеграл (2.6.7) вычисляется с помощью применения теоремы о

вычетах, на основании которой y(Ti)			i ,	если контур интегри-
рования охватывает полюс при z		. Таким образом, подходящим
контуром оказывается окружность радиусом				.
Рассмотрим z-преобразование от дискретной свѐртки, представ-
ленной в виде
	i
x(i)	h(s)y(i		s).	(2.6.8)
s	0

Пусть Y(z) – z-преобразование от y(Ti); H(z) – z-преобразование от h(Ti); Х (z) – z-преобразование от х(Ti). Рассмотрим произведение z-преобразований:

Y(z)H(z)	(y(0)	y(1)z 1 y(2)z 2 ...)
(h(0) h(1)z 1	h(2)z 2	...) y(0)h(0) z 1(y(0)h(1)
		74

y(1)h(0)) z 2(y(0)h(2) y(1)h(1) y(2)h(0)) ...,

из которого при условии (2.6.8) следует, что X(z) Y(z)H(z).

Рассмотрим z-преобразование от произведения двух последовательностей, которое представляется формулой

U(z)	x(Ti)y(Ti)z i .	(2.6.9)
i	0

Для X (z) – z-преобразования от x(Ti) и для Y(z) – z-преобразо- вания от y(Ti) запишем выражения для обратных z-преобразо-

ваний:
x(Ti)	1	X (v)vi 1dv, y(Ti)	1	Y(v)vi 1dv.
x(Ti)	2 j	X (v)vi 1dv, y(Ti)	2 j	Y(v)vi 1dv.
	2 j		2 j

Выберем контур интегрирования в виде единичной окружности. Будем иметь

U(z)	x(Ti)z i	1	Y(v)vi 1dv.
		2 j
i	0

Поменяв местами операции интегрирования и суммирования и рассматривая результирующее суммирование как z-преобразование, получим

U(z)	1	Y(v)X	z	v 1dv.
	2 j		v

Последнее равенство представляет собой теорему о комплексной свѐртке. Это действительно свѐртка, в чѐм можно убедиться, если использовать условие, что контур интегрирования представляет

собой	единичную окружность.					Сделаем	подстановки	v e j ,
z e j	и в результате получаем выражение в форме свѐртки
			1		2
	U(e j )				Y(e j )X (e j(		)d .	(2.6.10)
	U(e j )		2		Y(e j )X (e j(		)d .	(2.6.10)
			2		0
					0
Если сделать замены				T,		1T в (2.6.10), то получим свѐрт-
ки для частотных функций
		T	2 /T
	U(e j T )				Y(e j	1T )X (e j(	1)T )d .	(2.6.11)
	U(e j T )				Y(e j	1T )X (e j(	1)T )d .	(2.6.11)
		2					1
		2	0
			0
					75

Список вопросов для самопроверки к гл. 2

1.Какие основные характеристики гармонических и полигармонических сигналов приведены в разд. 2.1.1?

2.Какие основные характеристики колебательных сигналов с модулированными амплитудными и фазовыми функциями указаны

вразд. 2.1.2?

3.Какие основные характеристики колебательных сигналов с синусоидальной амплитудной и фазовой модуляцией приведены в разд. 2.1.2?

4.В чѐм состоит определение для полной энергии сигналов?

5.В чѐм отличие определений для средней и мгновенной мощности сигналов?

6.В чѐм состоят особенности вычисления средней мощности для полигармонических сигналов?

7.Какие варианты моделей наблюдений сигналов для задач ЦОС приведены в разд 2.3?

8.Какие варианты моделей сигналов приведены в разд. 2.3?

9.В чѐм состоит формулировка основной постановки и описание этапов задачи оценивания параметров сигналов на основе аппроксимации?

10.В чѐм состоит формулировка основной постановки и описание этапов задачи аппроксимации наблюдений для линейных моделей в действительном случае?

11.В чѐм состоит формулировка основной постановки и описание этапов задачи аппроксимации наблюдений для линейных моделей в комплексном случае?

12.В чѐм состоит формулировка основной постановки и описание этапов задачи построения моделей сигналов на основе действительного ряда Фурье?

13.В чѐм состоит формулировака основной постановки и описание этапов задачи построения моделей сигналов на основе комплексного ряда Фурье?

14.В чѐм состоит формулировка основной постановки и описание этапов вывода преобразования Фурье?

15.В чѐм состоит физический смысл преобразования Фурье?

16.Каковы основные свойства преобразования Фурье?

Список задач к гл. 2

1. Для приведенных ниже моделей указать параметры сигналов, входящие в состав вектора параметров; записать выражения для базисных функций; записать вид матрицы плана сигнала X; запи-

сать вид матрицы A XT X; сформировать вектор наблюдений Y; сформировать вектор коэффициентов Фурье b XTY; сформиро-

вать линейную систему Ac					b для вычисления оптимальных ли-
нейных коэффициентов модели. Модели:
1)	yM (c, Ti)	c1	c2Ti , i		0, 1,..., N		1;
2)	y (c, Ti)	c	c Ti	c (Ti)2 , i 0, 1,..., N					1;
	M	1	2	3
		m
3)	yM (c,Ti)		cr r (Ti),		i	0, 1,...,	N	1,	r (Ti) – дискретные
		r 1
базисные или		дискретные			базисные		ортогональные функции,
r 1,..., m;
		m	c (Ti)r 1,
4)	y (c, Ti)		c (Ti)r 1,		i	0, 1,..., N		1.
	M		r

2.Для приведенных ниже моделей указать параметры сигналов, входящие в состав вектора параметров; указать линейные и нелинейные параметры; фиксировать нелинейные параметры; записать выражения для базисных функций; записать вид матрицы плана

сигнала X; записать вид матрицы A XT X; сформировать вектор наблюдений Y; сформировать вектор коэффициентов Фурье b XTY; сформировать линейную систему Ac b для вычисле-

ния оптимальных линейных коэффициентов модели; записать выражение для остаточной суммы; сформировать процедуру подпоиска по нелинейным параметрам. Модели:

1)	yM (c, Ti)	acos	Ti	bsin	Ti,	i	0, 1,..., N		1;
2)	y (c, Ti)	acos( Ti		(Ti)2 / 2)			bsin(	Ti	(Ti)2 / 2),
	M
i 0, 1,..., N 1;
3)	y (c, Ti)	(A	BTi)cos( Ti			(Ti)2 /2),		i 0, 1,..., N 1;
	M
4)	y (c, Ti)	Ae	Ti cos( Ti		),	i	0, 1,..., N		1;
	M
					77

5)	y (c, Ti)	A e	T1i cos( Ti	1	)	A e 2Ti cos(	Ti	2	),
	M	1	1	1		2	2	2

i 0, 1,..., N 1;

6)	yM (c, Ti)	acos Ti	bsin	Ti d1	d2Ti,	i 0, 1,..., N 1;
		L
7)	yM (c, Ti)	(al cos	lTi	bl sin	lTi), i	0, 1,..., N 1.

3.Вычислить параметры моделей 1–5 для непрерывных сигналов на основе разложения в действительный ряд Фурье

y(t),	0 t T0 ,		yM (c, t)			a0	(al cos lt			bl sin lt),
y(t),	0 t T0 ,		yM (c, t)		2		(al cos lt			bl sin lt),
					2		l 1
							l 1
			l	l,			2	/ Т0,
	2 T0			l	0, 1, 2,...,				2	T0
al		y(t)cos	ltdt,					bl		y(t)sin ltdt,
al		y(t)cos	ltdt,					bl		y(t)sin ltdt,
	T0 0								T0 0

т.е. найти

1)y(t)

2)y(t)

3)y(t)

4)y(t)

5)y(t)

l	1,	2,...,		сT	(a ,		a ,..., b , b ,...),
						0	1	0	1
al , bl для:
1,0	t	T01,
0,T01	t	T0;
Acos(2 f0t			0),		0	t	T0;
t, 0	t	T0;
ty0 /(T0 /2),				0	t	T0 /2,
ty0 /(T0 /2)			2y0 ,		T0 /2		t	T0;
1 cos	2	t,	T /		t	T /2.
1 cos		t,	T /		t	T /2.
	T0		0			0
	T0

Глава 3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА СИГНАЛОВ

3.1.Оценивание статистических характеристик для стационарных и нестационарных сигналов

3.1.1. Определение статистических характеристик сигналов

Дадим определения для основных статистических характеристик случайных сигналов, используемых в практике ЦОС. Пусть случайный сигнал обозначается как Y(t), t , и его значе-

ния рассматриваются для некоторого момента времени ti . Тогда Y(ti ) будет представлять собой случайную величину. Для случайной величины Y(ti ) можно определить функцию одномерного за-

кона

распределения

вероятностей

F (y , t ) как

вероятность вы-

полнения неравенства

F (y , t ) P{Y(t ) y }.

i i

Функции

F (y , t )

являются

монотонно

неубывающими;

если

i i

то

должно

выполняться

соотношение

F (y

, t )

F (y

,t ). Из физических соображений, очевидно, справедливы

равенства

F (

, t )

F (

, t ) 1. Вероятность

выполнения

неравенства P{y1i

Y(ti )

y2i}

находится

с помощью

функции

F1(yi , ti ) :

P{y

Y(t ) y

} F (y

,t ) F (y

,t ).

1 2i

1 1i

Общий вид функции одномерного закона распределения вероятно-

стей F (y , t ) для некоторого момента времени t					i	представлен на
1 i i					i
рис. 3.1.1а.
Если функция F (y , t )	дифференцируема по					у , то вводится
1 i i						i
функция одномерной плотности распределения вероятностей
p (y ,t )			dF1(yi ,ti )	.
p (y ,t )				.
1	i i		dyi
			dyi
Вероятность выполнения неравенства P{y1i Y(ti )						y2i} находится
с помощью интегрирования функции р1(yi , ti ) :
		79

y2i

P{y1i Y(ti ) y2i}

p(yi ,ti )dyi .

y1i

Рис. 3.1.1а. Функция закона распределения случайной величины

Рис. 3.1.1б. Функция плотности распределения вероятностей случайной величины

Для функции р1(yi , ti ) должно выполняться вполне естественное равенство

p1(yi ,ti )dyi 1.

<<< < Предыдущая 1 2 3 4 5 6 78 / 248 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>