Пименов Ю.В., Муравцов А.Д. Техническая электродинамика, 2000

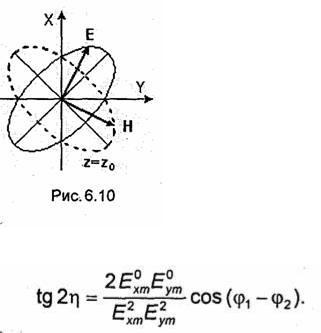
описывающему эллипс, большая ось которого повернута относительно оси. X на угол η (рис. 6.10), определяемый соотношением

В случае среды с потерями получается аналогичный результат. Отличие состоит" лишь в том, что величины полуосей эллипса зависят от координаты z (уменьшаются с увеличением z).

Таким образом, в общем случае, т.е. при произвольных φ1, φ2, Е°хт и Е°ут в фиксированной точке пространства (z) конец вектора Е описывает эллипс. Волны такого типа принято называть эллиптически поляризованными. Ориентация векторов Е, соответствующих различным значениям координаты z в фиксированный момент времени в среде без потерь, аналогична изображенной на рис. 6.9, б. Отличие состоит в том, что в данном случае проекция винтовой линии, соединяющей концы векторов Е, на плоскость XOY образует эллипс (рис.6.10).

Очевидно, что линейно поляризованная волна и волна с круговой поляризацией являются частными случаями эллиптически поляризованной волны. Отметим, что понятие линейной, круговой и эллиптической поляризации применимо не только для плоских, но и для других типов волн. Например, сферические волны, создаваемые в дальней зоне элементарным электрическим вибратором или элементарным магнитным вибратором, являются линейно поляризованными. Действительно, в случае ЭЭВ вектор Е колеблется в меридианальной плоскости, и в любой фиксированной точке пространства, принадлежащей дальней зоне, его направление либо совпадает с направлением вектора θ0, либо противоположно ему. Аналогично в случае элементарного магнитного вибратора вектор Е лежит в азимутальной плоскости, и в любой фиксированной точке направлен либо так же, как вектор ф0, либо противоположно ему.

Волны, созданные более сложными излучателями, могут иметь и круговую, и эллиптическую поляризацию. Например, сферическая волна, создаваемая в дальней зоне двумя взаимно перпендикулярными элементарными электрическими вибраторами, токи которых равны по величине и сдвинуты по фазе на π/2, в направлении, перпендикулярном обоим вибраторам, будет иметь круговую поляризацию.

При определении поляризации волны до сих пор рассматривался только вектор Е. Очевидно, такой же анализ для вектора Н привел бы к аналогичным результатам. В общем случае (при произвольных начальных фазах и амплитудах) конец вектора Н в фиксированной точке пространства с течением времени также описывает эллипс, подобный эллипсу вектора Е и повернутый относительно него на угол π/2 (рис.6.10). В рассмотренных выше частных случаях линейной и круговой поляризацией этот эллипс вырождается соответственно в отрезок прямой линии и окружность.

151

Отметим, что в тех случаях, когда анализируемая плоская волна является неоднородной (т.е. когда поверхности равных амплитуд не совпадают с поверхностями равных фаз), поляризация волны может быть различной в разных точках плоскости, перпендикулярной направлению распространения волны (оси Z). Это объясняется тем, что амплитуда неоднородной плоской волны зависит от координат х и у и при изменении последних может изменяться соотношение между составляющими Ех и Еу. Кроме того, поляризация неоднородной волны, определенная по вектору Е, может не совпадать с поляризацией волны по вектору Н.

Выясним условие взаимной перпендикулярности векторов, Е и Н плоской волны. В общем случае имеют место соотношения

Для ортогональности векторов необходимо, чтобы их скалярное произведение было равно нулю. Правая часть равенства (6.45) обращается в нуль только в следующих частных

случаях: при Первый случай соответствует линейно поляризованной волне, а второй - среде без потерь.

Таким образом, в общем случае векторы Е и Н в среде с потерями не перпендикулярны друг другу. Это вызвано тем, что в среде с потерями векторы Е и Н изменяются несинфазно.

152

Глава 7 ВОЛНОВЫЕ ЯВЛЕНИЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД

7.1. ПОЛЕ ОДНОРОДНОЙ ПЛОСКОЙ ВОЛНЫ, РАСПРОСТРАНЯЮЩЕЙСЯ В ПРОИЗВОЛЬНОМ НАПРАВЛЕНИИ

Ранее рассматривалось распространение электромагнитных волн в однородных средах. Однако при решении многих практически важных задач нельзя считать, что среда является однородной. На структуру поля и характер распространения волны существенно влияет граница раздела сред, обладающих разными свойствами. Попадая на поверхность раздела двух сред, электромагнитная волна может частично (или полностью) отразиться либо частично (либо полностью) пройти в другую среду. Кроме того, возможно и более сложное явление, называемое дифракцией волн (см. гл.8).

Определение поля, возникающего при падении какой-либо электромагнитной волны на границу раздела двух сред, в общем случае (при сложной форме поверхности раздела) сопряжено с большими математическими трудностями. В данном разделе рассматривается простейшая задача такого типа: падение плоской электромагнитной волны на плоскую бесконечно протяженную границу раздела двух однородных изотропных сред. При анализе распространения плоской электромагнитной волны в неограниченной однородной среде была использована прямоугольная система координат, одна из осей которой (ось Z) совпадала с направлением распространения волны.

Для изучения волновых явлений на границе раздела двух сред систему координат обычно вводят таким образом, чтобы поверхность раздела совпадала с одной из координатных поверхностей. При этом в общем случае направление распространения волны не совпадает ни с одной из координатных осей.

Ограничимся рассмотрением линейно поляризованных волн, так как волны круговой и эллиптической поляризации можно представить в виде суперпозиции двух линейно поляризованных плоских волн (см. 6.2). Предположим, что волна распространяется в однородной изотропной среде вдоль оси Z', образующей с осями X, У, Z прямоугольной системы координат углы φ хφ y φz соответственно (рис. 7.1). Поле однородной плоской волны в среде без потерь (см. 6.1) можно представить в виде

удовлетворяют уравнению z' = (r, z0') = const, где r - радиус-вектор, проведенный из начала координат до произвольной точки, лежащей на рассматриваемой ПРФ. Для перехода к координатам х, у, z нужно вычислить скалярное произведение вектора r на вектор z0'. Учитывая, что r = xоx + yоy + zoz, запишем

153

Прежде чем перейти к анализу волновых явлений на границе раздела двух сред, введем некоторые определения. Назовем плоскость, проходящую через нормаль к поверхности раздела двух сред параллельно направлению распространения волны, плоскостью падения. Вектор напряженности электрического поля плоской волны перпендикулярен направлению ее распространения, а по отношению к плоскости падения может быть ориентирован произвольно. Однако, не нарушая общности анализа, можно ограничиться рассмотрением двух ориентации вектора Е, а именно:

вектор Е перпендикулярен плоскости падения (нормально поляризованная плоская волна); вектор Е параллелен плоскости падения (параллельно поляризованная плоская волна). Очевидно, что волну с любой другой ориентацией вектора Е, а также волны, имеющие круговую или эллиптическую поляризацию, можно представить в виде суперпозиции двух волн, одна из которых является нормально поляризованной, а вторая - параллельно поляризованной.

7.2. ПАДЕНИЕ НОРМАЛЬНО ПОЛЯРИЗОВАННОЙ ПЛОСКОЙ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА ДВУХ СРЕД

Пусть линейно поляризованная плоская электромагнитная волна падает на плоскую бесконечно протяженную границу раздела двух однородных изотропных сред,

характеризуемых параметрами 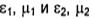соответственно. Введем прямоугольную систему координат х, у, z так, чтобы плоскость YOZ совпадала с поверхностью раздела, а плоскость падения - с плоскостью XOZ. Угол φ между направлением распространения волны и нормалью к поверхности раздела будем называть углом падения (рис. 7.2).

В выбранной системе координат направляющие косинусы, определяющие направление распространения волны,

154

Отметим, что постоянная Ёо равна значению комплексной амплитуды у-й составляющей напряженности электрического поля в начале координат (при x = z=0). Соответственно векторная постоянная Ёо = у0 Ёо равна значению комплексной амплитуды вектора Е в начале координат.

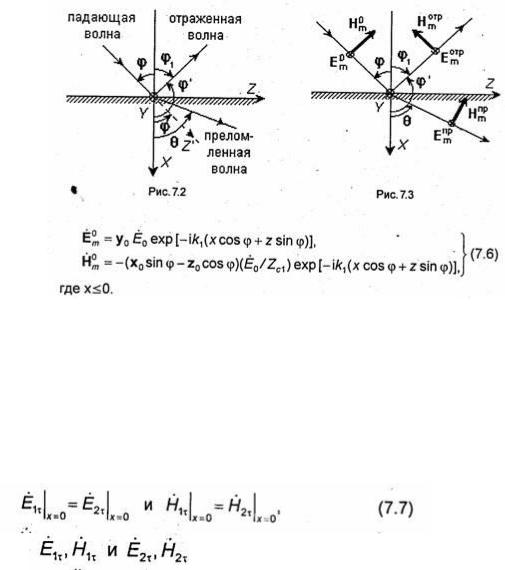
Из физических соображений очевидно, что падающая волна может частично (или полностью) отразиться от границы раздела (х = 0) и частично (или полностью) пройти во вторую среду. Естественно предположить, что отраженная и преломленная волны будут плоскими.

Если, исходя из этого предположения, удастся найти поле, удовлетворяющее граничным условиям

где - касательные составляющие векторов Ё и Н в первой и во второй средах соответственно, то это поле будет решением рассматриваемой задачи. Граничные условия (7.7) должны выполняться на всей плоскости х = 0, т.е. при любых значениях переменных у и z. Так как поле падающей волны (7.6) не зависит от переменной у, то необходимо предположить, что поле отраженной и преломленной волн также не зависит от координаты у. Это означает, что векторы, определяющие направление распространения отраженной и преломленной волн, параллельны плоскости XOZ. Можно также предположить, что отраженная и преломленная волны являются нормально поляризованными (рис.7.3). С учетом сделанных предположений выражения для векторов

поля отраженной волны могут быть получены из формул (7.6), если в пос-

ледних заменить 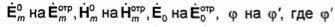-угол между осью X и

направлением распространения отраженной волны (см. рис.7.2 и 7.3), a - некоторая, пока неизвестная постоянная, равная значению комплексной амплитуды у-й составляющей напряженности электрического поля отраженной волны. Обычно вместо угла φ' рассматривают угол φ1=π-φ’, называемый

углом отражения. Так как При этом

155

характеристическое сопротивление волны во второй среде, а-некоторая, постоянная, равная значению комплексной амплитуды у-й составляющей напряженности электрического поля преломленной волны. Ориентация векторов Ёт и Нт падающей, отраженной и преломленной волн показана на рис.7.3. Углы φ1 и θ так же, как и постоянные

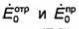подлежат определению.

Граничные условия (7.7) должны выполняться при всех значениях координаты г. Это возможно только, в том случае, если зависимость векторов Ё и Н от переменной z во всех трех волнах будет одинаковой. Поэтому необходимо, чтобы

Так как углы φ и φ1 заключены в интервале [0, π/2], то из равенства (7.10) следует первый закон Снеллиуса φ = φ1 ("УГОЛ падения равен углу отражения"). Из равенства (7.11) вытекает соотношение sin θ/sin φ = k1/k2, которое в случае идеальных однородных изотропных сред выражает второй закон Снеллиуса

("Отношение синуса угла преломления к синусу угла падения равно относительному показателю преломления сред n12"). Действительно, коэффициент преломления среды п = c0 /c, где с0 =

Отметим, что соотношение (7,11) остается верным и в случае проводящих сред. Пусть, например, первая среда - идеальный диэлектрик, а вторая обладает проводимостью, отличной от нуля. Тогда параметр k2 будет комплексной величиной, a k1 и угол φ останутся вещественными. Для выполнения равенства (7.11) при этом придется считать величину θ комплексной, не имеющей простого геометрического смысла (см. 7.6).

Для определения постоянных А и В используем граничные условия (7.7). Так как поле в первой среде складывается из полей падающей и отраженной волн, а поле во второй среде совпадает с полем преломленной волны, то формулы (7.7) принимают вид

Подставляя в эти выражения значения соответствующих составляющих комплексных амплитуд напряженности электрического и магнитного полей и учитывая равенства (7.10) и (7.11), приходим к соотношениям

156

называют коэффициентами Френеля. Символ означает, что рассматриваются нормально поляризованные волны. Деля обе части уравнений (7.13) на Ео, получаем

Решая эту систему уравнений, находим значения коэффициентов Френеля для случая нормальной поляризации:

В формулах (7.15) и (7.1б) можно исключить угол преломления 6, выразив cosG через

синус угла падения: Указанные формулы справедливы и в том случае, если одна из сред (или обе среды) обладают проводимостью. При этом диэлектрическая проницаемость соответствующей среды будет комплексной величиной, определяемой соотношением (1.61). Комплексными также будут соответствующие

параметры k и Zc,.a следовательно, и коэффициенты

Как видно из формул (7.14), модуль коэффициента отражения представляет собой отношение амплитуд напряженностей электрических полей отраженной и падающей волн в точке отражения (в рассматриваемом случае в любой точке границы раздела сред), а его аргумент равен разности фаз этих напряженностей в той же точке. Аналогично определяются модуль и аргумент коэффициента прохождения: в этом случае нужно только вместо отраженной волны рассматривать преломленную волну.

В тех случаях, когда проводимостью обладает только вторая среда, а магнитные проницаемости обеих сред одинаковы, формулу (7.16) обычно записывают в несколько иной форме. Пусть, например, первая среда - воздух (ε1= ε0), тогда выражение (7.16) может быть переписано в виде

где η = π/2 — φ — угол между направлением распространения падающей волны и

плоскостью раздела; - комплексная относительная диэлектрическая проницаемость второй среды.

Для расчета электромагнитного поля, возникающего в результате падения на плоскую границу раздела двух сред нормально поляризованной плоской волны в первой

157

среде, достаточно сложить поля, определяемые формулами (7.6) и (7.8). При этом в

формулах (7.8) нужно заменить φ1на φ и учесть соотношение 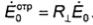Во второй среде искомое поле совпадает с полем преломленной волны и может быть рассчитано по

7.3. ПАДЕНИЕ ПАРАЛЛЕЛЬНО ПОЛЯРИЗОВАННОЙ ПЛОСКОЙ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА ДВУХ СРЕД

Предположим теперь, что волна, падающая на границу раздела (х = 0), является параллельно поляризованной. В этом случае вектор напряженности электрического поля падающей волны Е°т параллелен плоскости падения (у=0), а вектор напряженности магнитного поля Н°т ей перпендикулярен (рис.7.4). Анализ этого случая можно провести по аналогии с уже рассмотренным случаем нормальной поляризации или на основе перестановочной двойственности уравнений Максвелла (см.2.6). Используем второй путь.

Формулы, определяющие поле падающей волны, получаются из формул (7.6), если в последних в соответствии с перестановочной двойственностью уравнений Максвелла заменить

Выражения для коэффициентов Френеля 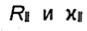в случае паралелльной поляризации могут быть получены непосредственно из формул (7.16) и (7.17), соответствующих

нормальной поляризации. Для упрощения изложения величины 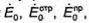относящиеся к случаям нормальной и параллельной поляризаций, будем обо-

158

159

Как видно, коэффициенты Френеля 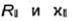существенно отличаются от коэффициентов R± и хх соответственно, т.е. отражение волны от границы раздела и прохождение во вторую среду зависят от поляризации падающей волны.

Отметим, что сделанное выше замечание о коэффициентах

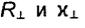в случае, когда одна из сред (или обе среды) обладает проводимостью, в

полной мере относится и к коэффициентам . Если магнитные проницаемости сред одинаковы, а проводимостью обладает только вторая среда, формулу (7.21) обычно записывают в несколько иной форме. Например, если первая среда - воздух (εr1 = 1), выражение (7.21) принимает вид

Очевидно, что для расчета поля в первой среде достаточно сложить поля, определяемые

формулами (7.18) и (7.19), и учесть, что Поле во второй среде совпадает с полем преломленной волны и может быть рассчитано по формулам (7.20), в которых

нужно учесть, равенство и второй закон Снеллиуса.

В случае нормального падения плоской волны теряет определенность понятие плоскости падения и, следовательно, исчезает различие между нормально Поляризованными и параллельно поляризованными волнами. Так как в этом случае φ = 0 и θ = 0, то коэффициенты Френеля принимают вид

7.4. ПОЛНОЕ ПРОХОЖДЕНИЕ ВОЛНЫ ВО ВТОРУЮ СРЕДУ

При определенных условиях падающая волна без отражения полностью проходит во вторую среду. Угол падения, соответствующий этому случаю, называют углом Брюстера. Условия, при которых отсутствует отраженная волна, могут быть установлены путем

решения уравнений 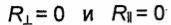относительно угла падения φ. В частном случае, когда обе среды являются немагнитными диэлектриками, угол Брюстера φ Бр легко находится из физических соображений.

160