Пименов Ю.В., Муравцов А.Д. Техническая электродинамика, 2000

наводятся электрические токи, на поддержание которых расходуется электромагнитная энергия. Вычислим соответствующую этому процессу среднюю за период мощность джоулевых потерь. Запишем уравнение баланса средних за период значений мощности для объема V, занимаемого рассматриваемым объектом. Учитывая, что внутри объема V нет сторонних источников, приходим к равенству 0 = РПср + PΣcp, из которого следует, что

где n0-орт внешней нормали к поверхности рассматриваемого объекта S. Как видно, для определения мощности Рпср нет необходимости вычислять поле внутри объекта, достаточно проинтегрировать по S перпендикулярную к ней составляющую комплексного вектора Пойнтинга. Знак минус в формуле (7.54) объясняется тем, что джоулевы потери определяются потоком энергии, направленным внутрь проводника, а орт п0 направлен из объема V в окружающее пространство. Нормальная составляющая вектора Пойнтинга определяется касательными составляющими векторов

Где μ2 и σ2 - абсолютная магнитная проницаемость и удельная проводимость проводника. Таким образом, средняя за период мощность джоулевых потерь в проводнике

Как уже отмечалось, структура поля у поверхности реального проводника близка к структуре поля у такой же поверхности идеального проводника. Поэтому при вычислении потерь обычно

предполагают, что Это предположение существенно упрощает расчеты, обеспечивая достаточную для инженерной практики точность результатов.

7.8.3. Эквивалентный поверхностный ток

Так как на высоких частотах ток фактически сосредоточен в тонком слое у поверхности проводника, часто оказывается удобным заменить реальное распределение тока эквивалентным поверхностным током. Для определения плотности этого эквивалентного поверхностного тока js предположим, что проводящее тело занимает все нижнее полупространство (рис.7.8). Выделим мысленно в нем "брусок" толщиной l, боковые грани которого параллельны вектору плотности тока j. Толщину l, выберем достаточно малой, чтобы в пределах l,плотность тока j и напряженность магнитного поля Н можно было считать неизменными. Так как в хорошо проводящей среде плотность тока смещения пренебрежимо мала по сравнению с плотностью тока проводимости, то полный ток, протекающей в выделенном "бруске", можно считать равным

171

где Г - контур поперечного сечения "бруска".

Так как по предположению векторы j и Н в пределах l, не меняются,

то интегралы по линиям, перпендикулярным поверхности тела, равны по величине и противоположны по знаку. Кроме того, поскольку в точках, бесконечно удаленных от поверхности тела напряженность магнитного поля равна нулю, получаем, что интеграл в формуле (7.57) равен интегралу по отрезку АВ на рис7.78:

Если считать, что весь ток течет по поверхности проводника, то значение i в формуле (7.59) равно поверхностному току. Его плотность jS = i/ l= Н° или в векторной форме

Это выражение аналогично граничному условию для касательной составляющей напряженности магнитного поля на поверхности идеального проводника.

7.8.4. Поверхностное сопротивление проводника

Касательная составляющая напряженности электрического поля на поверхности металла Ё1τи плотность эквивалентного поверхностного тока js направлены одинаково. Следовательно, можно записать

Коэфффициент пропорциональности Zs принято называть поверхностным сопротивлением проводника. Учитывая формулу (7.60) и граничное условие ЛеонтовичаЩукина (7.52), получаем, что поверхностное сопротивление

Активная часть поверхностного сопротивления

Из этого выражения следует, что проводник, заполняющий все полупространство, имеет в результате поверхностного эффекта такое же сопротивление, как и слой проводника толщиной 0 без учета поверхностного эффекта (отсюда и термин "глубина проникновения").

172

Отметим, что среднюю за период мощность потерь в проводнике [формула (7.57)] можно выразить также через эквивалентный поверхностный ток и активную часть поверхностного сопротивления:

7.8.5. Сопротивление цилиндрического проводника Случай резко выраженного поверхностного эффекта. Сопротивление цилиндрического

провода при переменном токе отличается от его сопротивления при постоянном токе. Это отличие обусловлено поверхностным эффектом. При одной и той же частоте поверхностный эффект будет проявляться тем сильнее, чем больше диаметр провода по сравнению с 0.

Рассмотрим сначала случай сильно выраженного поверхностного эффекта (толстый проводник). Пусть по цилиндрическому проводу радиуса а распространяется бегущая волна тока. Выделим достаточно малый элемент провода длины l, в пределах которого можно считать, что амплитуда тока не меняется. Предположим, что радиус провода а значительно превышает глубину проникновения (а» Δ°). В этом случае при определении сопротивления провода можно использовать результаты предыдущего раздела.

Комплексное сопротивление провода на единицу длины определяется формулой

где im - комплексная амплитуда тока в проводе, а Ům-комплексная амплитуда напряжения на концах отрезка провода длины l Совместим ось Z цилиндрической системы координат с осью провода. Тогда d1 = z0dl,

Подставляя выражения (7.66) в (7.65) и учитывая соотношения (7.61) и (7.62), получаем

Сопротивление Z можно выразить через активное сопротивление R и внутреннюю индуктивностьLi, приходящиеся на единицу длины провода: Z = R+iωL/. Отделяя в (7.67) действительную и мнимую части, находим R и L:

Из сравнения значений R и Li- при переменном токе с их значениями

при постоянном токе (см.4.6) следует, что отношение RIRo с ростом частоты увеличивается, а отношение Li/Li,o, наоборот, уменьшается. Полученные формулы можно использовать только при условии а»Δ ° Если это условие не выполняется, то для того, чтобы определить сопротивление провода, нужно найти его внутреннее поле.

Сопротивление провода с учетом его внутреннего поля. Введем цилиндрическую систему координат τ, φ, z, ось Z которой совпадает с осью рассматриваемого уединенного провода. Комплексную амплитуду плотности тока в проводе можно представить в виде

где b - комплексная постоянная, характеризующая распространение волны тока (электромагнитной волны) вдоль провода. Отметим, что постоянная, b связана с постоянной распространения γ, используемой в электротехнике, соотношением ехр (- ibz) = ехр (-γz) или b=-iγ. Известно (см., например, [13], что постоянная b по абсолютной величине близка к волновому числу

173

соответствующему среде, окружающей провод. Комплексная амплитуда продольной составляющей напряженности электрического поля внутри провода записывается

где J(k2r) и N0(k2r) -соответственно функции Бесселя и Неймана нулевого порядка, а А и В - произвольные постоянные. При r=0 (т.е. на оси провода) функция J0(k2r) является ограниченной, a N0(k2r) обращается в бесконечность. Поэтому в выражение (7.69) нужно положить B = 0. Для сокращения формул

174

Подставляя это выражение в (7.72), приходим к формуле (7.67). В случае тонких проводов, для которых а«:Δ°, модуль аргумента функций Бесселя |k2а|«1- Используя асимптотическое представление функциий Бесселя для малых значений аргумента

Множитель 1/(πа2σ2) в формуле (7.73) совпадает с сопротивленцем проводника при постоянном токе. Так как по предположению а«Δ°, то поправочный коэффициент будет мал по сравнению с единицей. Как и следовало ожидать, поверхностный эффект в этом случае проявляется слабо.

Отметим, что полученные в данном разделе формулы для погонного сопротивления провода верны в случае уединенного провода. Если линия состоит из нескольких параллельных проводов, то распределение тока по сечению провода нельзя считать осесимметричным. Учет несимметричного распределения тока приводит к увеличению погонного активного сопротивления. Однако если расстояние между проводами значительно больше диаметра провода, то поправка получается небольшой и ею можно пренебречь.

175

Глава 8

ДИФРАКЦИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН 8.1. Строгая постановка задач дифракции

Вгл.7 анализировалась структура электромагнитного поля, возникающего при падении однородной плоской волны на плоскую границу раздела двух сред. Однако во многих практически важных случаях поверхность раздела нельзя считать безграничной плоскостью, а падающую волну - плоской.

При падении электромагнитной волны на тело конечных размеров (или на край полубесконечного тела) помимо отражения и преломления (см. гл.7) также имеет место более сложное явление, называемое дифракцией. Поэтому задачи определения влияния различных объектов на структуру электромагнитного поля часто называют задачами дифракции. С необходимостью их решения, встречаются при проектировании и анализе антенных устройств, при исследовании распространения радиоволн в неоднородных средах, в радиолокации и др.

Внастоящей главе излагаются некоторые методы решения задач дифракции монохроматических электромагнитных волн на металлических телах, расположенных в безграничной однородной изотропной среде. Поле Ё°,Н° падающей волны (его называют первичным) считается известным. Для простоты предположим, что возбуждаемое этой волной тело является идеально проводящим, а в окружающей его среде (она характеризуется параметрами ε И μ )отсутствуют потери энергии. Под действием первичного поля на поверхности S тела возникают электрические токи, которые создают

вторичное электромагнитное поле Ёт,Нт. Так как первичное поле известно, то задача сводится к определению вторичного поля, причем достаточно найти один из его векторов

Ёт или Нт, так как любой из них можно однозначно выразить через другой непосредственно из уравнений Максвелла для монохроматического поля.

Во внешнем, по отношению к поверхности S пространстве вектор Ё удовлетворяет однородному уравнению Гельмгольца (2.33), в котором надо положить

На поверхности S касательная составляющая напряженности полного электрического поля Ё° +Ё должна быть равна нулю. Следовательно,

где п0 - единичная нормаль к поверхности S.

Кроме того, должно выполняться определенное условие в бесконечно удаленных точках. Если поверхность S имеет ограниченные размеры, в качестве такого условия можно использовать условие излучения (2.23).

Если рассматриваемое тело не имеет острых кромок (ребер), то сформулированная выше задача имеет единственное решение. При их наличии для единственности решения в общем случае требуется ввести дополнительное условие (условия на ребре), определяющее поведение составляющих векторов Ё и Н вблизи острой кромки (см. 2.2.3). Следует отметить, что решение многих задач существенно упрощается, если ввести некоторые вспомогательные функции (например, векторный потенциал А, вектор Герца Г и др.).

При построении решения задачи дифракции электромагнирных волн в строгой постановке ее обычно сводят либо к дифференциальному уравнению (уравнению Гельмгольца), либо к интегральным (в общем случае интегро-дифференциальным) уравнениям. В некоторых простейших случаях удается найти аналитическое решение, в остальных-решение может быть построено только на основе численных методов. Рассмотрим указанные подходы на примере некоторых простых задач дифракции.

8.2. ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА КРУГОВОМ ЦИЛИНДРЕ

176

Пусть плоская линейно поляризованная электромагнитная волна падает на идеально проводящий круговой цилиндр радиуса а перпендикулярно его оси (рис. 8.1). Введем цилиндрическую систему координат r, φ, z, ось Z которой совпадает с осью цилиндра, а угол φ отсчитывается от оси X, противоположной направлению распространения волны.

При решении задачи можно ограничиться рассмотрением двух типов поляризации падающей волны относительно оси цилиндра:

а) вектор Ё° параллелен оси Z, б) вектор Н° параллелен оси Z.

Любую другую ориентацию векторов Ё° и Н° первичного поля можно представить как суперпозицию этих случаев. Остановимся подробнее на первой задаче, так как вторая решается аналогично. Напряженность электрического поля падающей волны имеет

только z-ю составляющую

Рассматриваемая задача является двумерной (отсутствует зависимость от переменной z), поэтому уравнение (2.33) для напряженности вторичного электрического поля, которая также будет

иметь лишь z-ю составляющую (Ёт = z0 Ё(r, φ)), принимает вид

Функция Е на поверхности S должна удовлетворять граничному условию (8.1), которое в рассматриваемом случае принимает вид

Ё(а, φ) = -Е0 ехр(ika cosφ), (8.4)

а в бесконечно удаленных точках - условию излучения. Это условие, по существу, состоит в следующем. При r→∞ в выражение для функции Ё(r,φ) должны входить составляющие с фазовым множителем вида ехр (- ikr), которые соответствуют волне, уходящей в бесконечность от оси Z; составляющие же с фазовым множителем ехр (ikr), которые соответствуют волне, распространяющейся из бесконечности к оси Z, должны отсутствовать.

Для решения задачи применим метод Фурье (см. 3.5.3, где этим методом решена задача Дирихле для прямоугольной области). Представим функцию Ё(r,φ) в виде

Подставим эту формулу в уравнение (8.3) и умножим обе его части на r2.Выполним дифференцирование и разделим затем получающееся уравнение почленно на произведение RФ:

177

Левая часть полученного уравнения зависит только от переменной r, а правая - только от переменной φ. Переменные r, и φ являются независимыми. Следовательно, уравнение (8.5) представляет собой равенство двух независимых функций. Это возможно только при условии, что каждая из функций равна постоянной. Обозначая последнюю через т2, приходим к двум независимым дифференциальным уравнениям:

Очевидно, что при изменении угла φ на 2π значение искомой функции Е(r, π) должно остаться прежним:

Условие (8.8) можно переписать для функции Ф:

Решение уравнения (8.6) имеет вид

где А и В - произвольные постоянные.

Условие (8.9) выполняется, если т - целое число (т=0,1,2,...). Напряженность первичного электрического поля - четная функция относительно угла φ. Поэтому можно предположить, что функция Е, а следовательно, и функция Ф также должны быть четными относительно угла φ. Таким образом, постоянная А = 0 и

Уравнение (8.7) является уравнением Бесселя. Его решение можно представить в виде

где Jm(kr) и N m(kг) - функции Бесселя т-го порядка первого и второго рода соответственно (функцию Nm(kr) часто называют также функцией Неймана m-го порядка), а С’ и С’ - произвольные постоянные.

В рассматриваемом случае решение уравнения (8.7) удобнее выразить через функции Бесселя третьего рода - функции Ханкеля:

Неймана и Ханкеля часто называют также цилиндрическими функциями первого, второго и третьего рода соответственно.

178

распространяющейся из бесконечности к оси Z, а функция цилиндрической волне, распространяющейся от оси Z к бесконечности вдоль радиусов r. Следовательно, для выполнения условия излучения необходимо считать, что постоянная С = 0, при этом

формула (8.11) принимает вид Таким образом, решением уравнения (8.3), удовлетворяющим условию излучения, может служить функция

где Dm - некоторая постоянная.

Осталось выполнить граничное условие (8.4). Для этого -представим искомое решение Е(г, ср) в виде суперпозиции всех возможных функций (8.12):

Очевидно, выражение (8.13) является четной функцией, периодической по углу φ с периодом 2π, которая удовлетворяет условию излучения и уравнению (8.3). Коэффициенты Dm - пока произвольные постоянные. Требуется определить их таким образом, чтобы выполнялось условие (8.4). Подставим функцию (8.13) в (8.4) и воспользуемся известной из теории бесселевых функций формулой [24]:

Соотношение (8.14) можно получить, например, разлагая функцию exp (ika cos φ) в обычный ряд Фурье. Подставляя (8.13) и (8.14) в (8.4), приходим к равенству

Левую и правую части этого равенства можно рассматривать как разложение одной и той же функции в ряд Фурье. Так как такое разложение единственно, то коэффициенты разложения должны быть равны и, следовательно,

Подставляя формулы (8.15) в (8.13), получаем окончательное выражение для напряженности вторичного электрического поля, возникающего при падении плоской волны на идеально проводящий цилиндр радиуса а:

179

Ряд в выражении (8.16) является абсолютно сходящимся, его можно почленно дифференцировать. Поэтому данное выражение позволяет также найти напряженность вторичного магнитного поля (Hm =[i/(ωμ)]rotEm) и распределение токов на поверхности цилиндра.

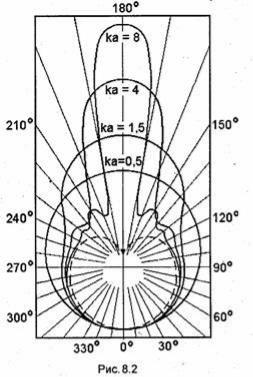
На рис. 8.2 показана зависимость модуля комплексной амплитуды напряженности

вторичного электрического поля Ет в дальней зоне в зависимости от угла φ при постоянном значении переменной r (отношение |Ёт(r,φ)|/│Ет(r,0)│) для различных

значений kа. Пунктирная кривая соответствует данным, рассчитанным на основе геометрической оптики (см. 8.5).

Как видно из графиков, в результате дифракции появляется вторичное поле с четко выраженным максимумом в направлении φ=180°.

Решение задачи в форме (8.16) в принципе пригодно для цилиндра любого радиуса. Однако при больших значениях параметра kа, т.е. если диаметр цилиндра велик по сравнению с длиной волны (kа = 2πа/λ), ряд в (8.16) сходится медленно и решение становится неудобным для анализа. Поэтому в случае k>>1 обычно стремятся получить более простые (но достаточно точные для практических целей) асимптотические формулы.

Изложенный строгий метод решения задачи дифракции называют методом Фурье. Однако такое решение удается получить лишь для тел простейшей конфигурации (например, круговой и эллиптический цилиндры, полуплоскость, клин, бесконечно протяженная бесконечно тонкая полоса конечной ширины, сфера, круговой конус, эллипсоид вращения, бесконечно тонкий диск и др.). Это связано с ограничениями, лежащими в основе метода Фурье. Для его применения необходимо, чтобы поверхность рассматриваемого тела полностью совпадала с какой-либо координатной поверхностью системы координат, в которой возможно разделение переменных в уравнении Гельмгольца. Если указанное условие не выполняется, для решения дифракционной задачи необходимо использовать другие методы.

8.3. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧ ДИФРАКЦИИ

180