Пименов Ю.В., Муравцов А.Д. Техническая электродинамика, 2000

металлическим телам, поверхность которых имеет изломы (ребра). Изложим основные принципы этого метода.

Пусть плоская электромагнитная волна падает на идеально проводящее тело, находящееся в однородной изотропной безграничной среде. Под действием этой волны на поверхности тела возникают электрические токи, которые создают вторичное поле. В физической оптике предполагается, что комплексная амплитуда плотности токов js, наведенных на поверхности тела S, равна

где Н°т - комплексная амплитуда напряженности магнитного поля падающей волны; n0 - орт внешней нормали к поверхности.S; So и S1 - освещенная и теневая части поверхности тела (очевидно, что So+ S1= S).

В действительности распределение токов на поверхности тела отличается от описываемого формулой (8.36). Представим вектор jSm в виде

Функцию jsm, можно рассматривать как комплексную амплитуду плотности некоторого

добавочного по отношению к 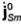тока, обусловленного искривлением поверхности тела. Искривлением называют любое отклонение поверхности тела от бесконечной плоскости: плавное искривление, излом, выступ, отверстие и т.д.

Составляющую принято называть равномерной частью

плотности тока, а составляющую jSm - соответственно неравномерной.

Учет только составляющей дает решение задачи в приближении физической оптики. Для получения более точного решения нужно учесть также составляющую jSm. Истинные значения функции jSm можно найти лишь при строгом решении рассматриваемой дифракционной задачи, что во многих случаях сопряжено с большими математическими трудностями. Поэтому приходится ограничиться определением приближенных значений jSm. В ряде случаев это можно сделать на основе упрощающих допущений.

Метод краевых волн позволяет находить приближенные значения составляющей jSm, обусловленной наличием ребер на поверхности выпуклого идеально проводящего тела, если его размеры и расстояние между ребрами велики по сравнению с длиной волны. Тогда можно предположить, что неравномерная часть тока отлична от нуля только в непосредственной близости от ребра. При этом распределение тока на малом элементе поверхности тела вблизи ее излома можно приближенно считать таким же, как на соответствующем идеально проводящем бесконечном двухгранном угле (клине), который образован плоскостями, касательными к поверхности тела в рассматриваемой точке ребра (сечение тела и соответствующего эквивалентного двухгранного угла было показано ранее на рис.2.4). Уфимцевым было проанализировано распределение тока на клине при возбуждении последнего плоской электромагнитной волной (данная задача имеет строгое решение) и получены удобные для расчетов формулы для электромагнитного поля, создаваемого неравномерной составляющей тока Анализ показал, что это поле имеет характер краевой волны (т.е. волны, распространяющейся от ребра клина). Полное поле записывается в виде суммы поля, найденного в приближении физической оптики, и поля указанных краевых волн.

Описанная методика решения дифракционных задач позволяет также учесть взаимное влияние соседних изломов поверхности тела. Для этого нужно считать, что краевая волна, соответствующая неравномерной части тока, распространяясь вдоль поверхности тела, достигает соседнего ребра и испытывает на нем дифракцию, возбуждая вторичные

191

краевые волны Последние, в свою очередь, порождают новые краевые волны и т.д. На основе метода краевых волн П. Я. Уфимцевым и другими авторами были найдены решения ряда практически важных задач. Численные расчеты показали, что полученные результаты удовлетворительно согласуются с результатами строгих решений (когда они могут быть получены) и экспериментальными данными. Подробнее этот метод изложен в

[22].

8.7. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ДИФРАКЦИИ 8.7.1. Дифракционные лучи

Геометрическая теория дифракции (ГТД) - один из наиболее эффективных методов асимптотического решения задач дифракции на телах сложной конфигурации, размеры которых велики по сравнению с длиной волны. Этот метод, предложенный Дж. Б. Келлером, является развитием и обобщением геометрической оптики. Как и геометрическая оптика, ГТД базируется на предположении, что энергия распространяется вдоль лучей, однако, в отличие от ГО в ней помимо падающих, отраженных и преломленных лучей вводятся так называемые дифракционные лучи. В случае идеально проводящих тел дифракционные лучи возникают при падении луча на ребро или острую вершину поверхности рассматриваемого тела, а также если падающий луч совпадает с касательной к плавно изогнутой поверхности.

Если падающий луч попадает на ребро тела, то возникает система дифракционных лучей, как бы образующих поверхность кругового конуса с вершиной в точке пересечения падающего луча с ребром Nо, называемой точкой дифракции (рис. 8.10). При этом ось конуса совпадает с касательной к ребру, а угол раскрыва конуса (2Р) равен удвоенному углу между падающим лучом и этой касательной. В тех случаях, когда падающий луч перпендикулярен касательной к ребру тела (рис. 8.11), коническая

поверхность вырождается в плоскость, перпендикулярную к ребру в точке дифракции. Если падающий луч попадает на острую вершину рассеивающего тела, то дифракционные лучи расходятся от нее во все стороны, как от точечного источника (рис. 8.12).

Если падающий луч совпадает с касательной к плавно изогнутой поверхности (рис. 8.13), то в точке касания (ее также называют точкой дифракции) оно расщепляется на два луча, один из которых является продолжением падающего, а второй скользит по поверхности тела вдоль геодезической линии, образуя "поверхностный" луч. В каждой точке от него отделяется прямолинейный дифракционный луч, совпадающий с касательной к поверхностному лучу в точке отрыва.

Таким образом, во всех случаях, когда возникают дифракционные лучи, наблюдается характерная особенность: один луч вызывает появление бесчисленного множества дифракционных лучей. Последние проникают в область геометрической тени и создают в ней некоторое поле. Кроме того, они изменяют поле в освещенной области.

Для определения поля в какой-либо точке пространства на основе ГТД нужно вначале найти все лучи, проходящие через данную точку, а затем вычислить поля, соответствующие каждому лучу, и просуммировать их. Иными словами, комплексную

192

амплитуду напряженности полного электрического поля в некоторой точке Л/ можно представить в виде

где комплексные амплитуды векторов напряженности электрических полей соответственно падающего, отраженного и дифракционного лучей в точке N. Аналогично записывается выражение для комплексной амплитуды напряженности полного магнитного поля в точке N.

Векторы вычисляются так же, как в ГО (см. 8.5). При определении вектора соответствующего одному дифракционному лучу, предполагается, что в точке дифракции Nо он пропорционален вектору падающего луча. Кроме того, как

обычно, предполагается, что фаза вектора изменяется линейно вдоль луча, а характер изменения амплитуды устанавливается из условия постоянства потока энергии вдоль соответствующей лучевой (энергетической) трубки. Эти предположения в равной

мере относятся и к вектору

8.7.2. Вычисление поля дифракционных лучей Дифракционные лучи, возникающие на ребре. Пусть появление дифракционных лучей

вызвано падением какого-либо луча на ребро идеально проводящего тела.

Комплексная амплитуда напряженности электрического поля дифракционного луча в точке N выражается через ее значение в некоторой точке Nо того же луча формулой, аналогичной (8.32). Однако в рассматриваемом случае в точке дифракции Nо один из главных радиусов кривизны (например, р2) обращается в нуль (р2→0 при N"0→No): ребро является особой линией (каустикой) для дифракционных лучей. Поэтому, устремляя

в выражении для точку Nо к Nо, получаем

193

В отличие от комплексных амплитуд которые, как это следует из формул (8.32) и (8.40), в точке Nо обращаются в бесконечность, величины СЕ(N0) и СН(NО) являются ограниченными.

Радиус кривизны ПРФ дифракционной волны зависит от формы ребра и направления падающего луча. Его можно вычислить для любой конфигурации ребра по формуле

где γ-угол между рассматриваемым дифракционным лучом и внутренней нормалью к ребру тела в точке Nо; β-угол между падающим лучом и касательной к ребру в точке Nо; ρ0 - радиус кривизны ребра в точке Nо, а β- производная угла р по длине дуги вдоль ребра в точке Nо (рис. 8.14).

Келлер предположил, что поле дифракционного луча связано с полем падающего луча в точке дифракции в случае криволинейного ребра практически так же, как в случае прямолинейного ребра. Поэтому указанная связь в случае идеально проводящего тела с криволинейным ребром, радиус кривизны которого ρо>>γ., может быть

установлена на основе анализа решения задачи дифракции плоской электромагнитной волны на идеально проводящем клине. В точке дифракции Nо ребро этого клина должно совпадать с касательной к ребру рассматриваемого тела, грани - с плоскостями, касательными к поверхности тела, а направление распространения плоской волны-с- направлением падающего луча, приходящего в точку Nо. Известно, что такая задача (при произвольном падении волны) сводится к анализу дифракции двух независимых плоских волн, в одной из которых вектор Н° перпендикулярен ребру клина,

а вектор Ё° имеет параллельную ребру составляющую (E-поляризация), а во второй - состав ляющую, параллельную ребру, имеет вектор Н° (Н - поляризация). При решении задачи можно ограничиться определением лишь

194

параллельных ребру клина составляющих векторов так как все остальные

составляющие векторов поля можно выразить через Соответственно можно ограничиться

записанных для случая прямолинейного ребра, с асимптотическими выражениями для тех же составляющих векторов поля, вытекающими из строгого решения задачи дифракции плоской электромагнитной волны на идеально проводящем клине. Келлером были получены следующие формулы:

угол эквивалентного клина (рис. 2.4), а φ0 и φ1 - соответственно углы между проекциями падающего и дифракционного лучей на плоскость, перпендикулярную к ребру тела в точке дифракции Nо, и линией пересечения этой плоскости с плоскостью, касательной к освещенной стороне поверхности тела в точке No (рис. 8.14). Формулы (8.45) не позволяют рассчитать поле вблизи границы "светтень": при φ1 = π ± <φ0 правая часть формулы (8.45) обращается в бесконечность. В дальнейшем были получены также выражения для коэффициентов дифракции, непрерывные на границе "свет-тень" (см., например, [23]).

Дифракционные лучи, возникающие на плавно изогнутой поверхности идеально проводящего тела. В этом случае (рис. 8.15) дифракционный луч состоит из двух частей: из отрезка (No-N1) геодезической линии и касательной к поверхности тела в точке N1 отрыва луча. Как обычно, предполагается, что фазы составляющих векторов поля изменяются линейно вдоль всего дифракционного лучa, а величины векторов поля дифракционного и падающего лучей пропорциональны. Коэффициенты пропорциональности также называют коэффициентами дифракции.

Векторы Ё°т и Н°т поля падающего луча в точке дифракции Nо

195

перпендикулярны к поверхностному лучу. Это поле в общем случае можно представить в виде двух волн, одна из которых имеет в точке Nо только касательную к поверхности тела (но перпендикулярную к поверхностному лучу!) составляющую комплексной амплитуды вектора напряженности электрического поля Ё°тτ и нормальную к поверхности тела составляющую комплексной амплитуды вектора напряженности магнитного поля Н°т, а

другая, наоборот, только составляющие Каждая из этих волн возбуждает свою поверхностную волну, распространяющуюся вдоль рассматриваемого поверхностного луча независимо от второй волны. Следовательно, вместо коэффициента

составляющими В качестве лучевой трубки выберем узкую полоску поверхностных лучей (рис. 8.15). Обозначим ее ширину в точке Nо через ∆σ0, а в точке N1 отстоящей от Nо на расстояние s, через ∆σ (s). Пусть средний за период поток энергии через поперечное сечение полоски ∆σ (s) равен Pcp(s), a через сечение ∆σ (s + ds) равен

Pcp(s+ds).

Как уже отмечалось, от поверхностного луча в каждой его точке отщепляется прямолинейный дифракционный луч, идущий вдоль касательной к поверхностному лучу в точке отрыва. Это эквивалентно излучению энергии с полоски поверхностных лучей. Предположим, что изменение потока энергии dP=Pcp(s + ds)- Pcp(s) на участке от s до s + ds вдоль выбранной лучевой трубки пропорционально потоку энергии Pcp(s) и длине участка ds, т.е. справедливо равенство

dP=-2αP(s)ds, (8.46)

где 2α - коэффициент пропорциональности, а знак"-" показывает, что поток энергии уменьшается вдоль луча. Величина α зависит от формы поверхности тела. Интегрируя формулу (8.46), находим

где Ро - средний за период поток энергии через сечение ∆σ0.

Переходя от P(s) к комплексной амплитуде напряженности электрического, поля поверхностного луча (в рассматриваемом случае имеется только составляющая Етп), получаем

Здесь ∆σ /∆σ (s) - отношение ширины полоски поверхностных лучей при s = 0 (т.е. в точке Nо) к ее ширине на расстоянии s от ∆σ 0 или, точнее, предел этого отношения, когда ширина полоски стремится к нулю. Вводя коэффициент дифракции

D(N0), перепишем выражение (8.48) в виде

Формула (8.49) определяет поле поверхностного луча в точке N1 через поле падающего луча в точке дифракции Nо.

Закон изменения амплитуды рассматриваемой составляющей вдоль прямолинейного луча N1→N устанавливается так же, как и в случае дифракционных лучей, возникающих на

196

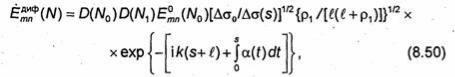
ребре. Предположим, что вектор напряженности электрического поля прямолинейного дифракционного луча в точке отрыва N1, пропорционален вектору напряженности электрического поля поверхностного луча в этой же точке. Коэффициент пропорциональности (коэффициент дифракции) обозначим через D(N1). Так как в рассматриваемом случае один из главных радиусов кривизны ПРФ, соответствующей прямолинейным дифракционным лучам, отщепляющимся от поверхностных лучей

(например, ρ2), в точке N1 равен нулю, то значение в точке N определяется выражением

где l - расстояние между точкой отрыва прямолинейного луча от поверхности тела (N1) и точкой наблюдения (N), аρ1- отличный от нуля радиус кривизны ПРФ дифракционной волны, соответствующей прямолинейным лучам, в точке N1.

Коэффициенты дифракции D(N0) и D(N1) должны одинаковым образом зависеть от свойств поверхности тела (и других параметров) в соответствующих точках, так как только в этом случае поле, определяемое формулой (8.50), будет удовлетворять теореме взаимности (см. 5.8).

Направление вектора Ёт в точке N такое же, как в точке N1, a

в точках поверхностного луча оно совпадает с направлением нормали к поверхности тела, т.е. изменяется вдоль луча.

Аналогично анализируется случай падения волны с другой поляризацией.

Для определения коэффициента дифракции и постоянной а Келлер предположил, что они определяются радиусом кривизны поверхности тела в плоскости падения (в плоскости, проходящей через нормаль к поверхности тела и падающий луч) и не зависят от других характеристик поверхности. Это позволило определить параметры D и α на основе анализа дифракции плоской волны на идеально проводящем круговом цилиндре.

Составляющим Етп и Етτ соответствуют разные коэффициенты дифракции и постоянные а. Более подробно вопрос о применении ГТД для анализа дифракции электромагнитных волн на гладких выпуклых телах, формулы для коэффициентов дифракции и постоянных а, а также другие проблемы ГТД рассмотрены в [23].

197

198

Глава 9

ОБЩИЕ СВОЙСТВА НАПРАВЛЯЕМЫХ ВОЛН 9.1. НАПРАВЛЯЮЩИЕ СИСТЕМЫ И НАПРАВЛЯЕМЫЕ ВОЛНЫ

Кроме свободно распространяющихся волн, рассмотренных в предыдущих главах, существуют волны, распространение которых возможно только при наличии каких-либо направляющих элементов (границы раздела сред, металлических, диэлектрических или полупроводящих трубок, стержней и др.). Такие волны называют направляемыми. Совокупность направляемых элементов образует направляющую систему. Направляющие системы служат для передачи энергии электромагнитной волны от источника (генератора) к потребителю например от передатчика к антенне, от приемной антенны ко входу приемника и т.д. В связи с этим направляющие системы называют также линиями передачи энергии или, более коротко, линиями передачи. Направляющую систему, у которой поперечное сечение и другие параметры не меняются в продольном направлении, называют однородной. На рис. 9.1 изображены поперечные сечения некоторых используемых на практике однородных направляющих систем: двухпроводной (а), коаксиальной (б), экранированной двухпроводной (в), симметричной (г) и несимметричной (д) полосковых линий, диэлектрического волновода (е), световода (ж) и полых металлических волноводов: прямоугольного (з), круглого (и) и эллиптического (к).

Все линии передачи можно разделить на два класса: линии открытого типа (см., например, рис.9.1,а,г,д,е,ж) и линии закрытого типа (см., например, рис.9.1,б,в,з,и,к). В линиях передачи закрытого типа вся передаваемая энергия сосредоточена в области, экранированной от внешней среды металлической оболочкой той или иной формы. В линиях открытого типа электромагнитное поле, строго говоря, распределено во всем пространстве, окружающем линию. Линии открытого типа обычно выполняют таким образом, чтобы подавляющая часть передаваемой энергии была сосредоточена в непосредственной близости к линии. Тем не менее линии открытого типа подвержены влиянию внешних воздействий. На волны в таких линиях влияют электромагнитные поля, созданные другими источниками, и внешние условия (например, метеорологические: дождь, снег, обледенение).

По структуре поля направляемые волны делятся на поперечные, электрические, магнитные и гибридные.

Поперечными волнами, или ТЕМ-волнами (Т- первая буква английского слова transvers, что означает поперечный), называют волны, у которых векторы Е и Н перпендикулярны направлению распространения волны, т.е. не имеют продольных составляющих. Отметим, что в соответствии с ГОСТ 18238-72 (Линии передачи сверхвысоких частот. Термины и определения) эти волны полагается называть 7-волнами. Однако это название практически

199

не используется ни в зарубежной, ни в отечественной литературе. Поэтому в книге сохранен общепринятый термин ТЕМ-волны.

Электрическими волнами, или Е-волнами, называют волны, у которых вектор Е имеет как поперечные, так и продольную составляющие, а продольная составляющая вектора Н равна нулю. Е-волны иногда называют поперечными магнитными волнами или ТМволнами.

Магнитными волнами, или Н-волнами, называют волны, у которых вектор Н имеет как поперечные, так и продольную составляющую, а продольная составляющая вектора Е равна нулю. Н-волны иногда называют поперечными электрическими волнами или ГЕволнами.

Гибридными, или смешанными волнами называют волны, у которых и вектор Е, и вектор Н наряду с поперечными составляющими имеют и продольные составляющие.

9.2. СВЯЗЬ МЕЖДУ ПОПЕРЕЧНЫМИ И ПРОДОЛЬНЫМИ СОСТАВЛЯЮЩИМИ ВЕКТОРОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Рассмотрим произвольную бесконечно протяженную однородную направляющую систему, ориентированную вдоль оси Z Будем считать, что направляющая система не вносит потерь.

В области, где отсутствуют сторонние источники, комплексные амплитуды векторов Е и Н, соответствующие волне, бегущей вдоль однородной линии передачи, могут быть представлены в виде

где β = const (коэффициент фазы), а ξ и η - координаты, изменяющиеся в поперечном сечении рассматриваемой линии передачи. Выбор конкретной системы координат зависит от формы поперечного сечения линии. Множитель exp(-iβz) соответствует волне, бегущей в положительном направлении оси Z, а множитель exp (iβz)-волне, бегущей в обратном направлении. Для определенности будем считать, что волна распространяется в положительном направлении оси Z. Если потребуется рассмотреть волны, бегущие в обратном направлении, это всегда будет оговорено.

Векторы Ёт и Нт должны удовлетворять однородным уравнениям Гельмгольца (2.32) и

(2.33) соответственно. С учетом формул (9.1) эти уравнения при могут быть переписаны в виде

а оператор Величину γ┴ называют поперечным волновым числом. Покажем, что в тех случаях, когда векторы ЁтиНт (оба или один из них) имеют продольные составляющие, нахождение поля направляемой волны

может быть сведено к определению составляющих Ётz и Hmz, так как поперечное составляющие векторов

поля выражаются через продольные. Проецируя уравнения Максвелла (1.76) на оси X и У декартовой дистемы координат и учитывая, что в рассматриваемом случае дифференцирование по переменной z эквивалентно умножению на (- iβ), получаем

Система уравнений (9.4) позволяет выразить составляющие Ётх,Ёту,Нтх и Нту через Ёmz и Нтz. После элементарных преобразований имеем .

200