Пименов Ю.В., Муравцов А.Д. Техническая электродинамика, 2000

Бурное развитие вычислительной техники позволило в последние десятилетия разработать и реализовать ряд численных методов решения задач дифракции электромагнитных волн. Среди этих методов наиболее универсальными являются методы, основанные на сведении задачи к интегральным или интегро-дифференциальным уравнениям. В качестве примера рассмотрим двумерную задачу дифракции электромагнитного поля, создаваемого токовой нитью (бесконечно протяженным прямолинейным электрическим током /0 , амплитуда и фаза которого одинаковы по всей длине) на идеально проводящей цилиндрической поверхности S произвольного профиля. Поперечное сечение поверхности S представляет собой кусочно-гладкий контур Г, который может быть как замкнутым, так и незамкнутым. В случае замкнутого контура Г поверхность S эквивалентна сплошному идеально проводящему цилиндру, а незамкнутый контур Г соответствует идеально проводящему бесконечно тонкому незамкнутому цилиндрическому экрану. Контур Г и используемая система декартовых координат х, у, z показаны на рис. 8.3. Токовая нить проходит через точку N0=N0( x0,yo) параллельно оси Z.

При отсутствии поверхности S токовая нить создает поле Ё°, Н°, которое будем называть первичным полем. Под его воздействием на S наводятся продольные (параллельные оси Z) поверхностные токи с плотностью js, которые создают вторичное поле Ё, Н. Комплексные амплитуды векторных потенциалов, создаваемых токовой нитью и токами, наведенными на S, определяются выражениями (2.63) и (2.64) соответственно. На поверхности S должно выполняться граничное условие

181

ζ ' и η'-производные функций ζ и η по t, а τ -значение переменной t, соответствующее точке наблюдения Мо Є Г. Функцию K(t, -τ) называют ядром интегрального уравнения

(8.19).

Как видно, переход к интегральному уравнению позволил понизить размерность задачи: вместо определения функции Ат, зависящей от двух переменных (координат х и у), задача сведена к нахождению функции jSm(t), зависящей от одной переменной t

Аналитическое решение уравнения (8.19) удается получить только в случае простейших контуров, таких как окружность, полупрямая и т.п. В более общих случаях решение уравнения (8.19) может быть построено только на основе численных методов (см., например, [18—21]).

Рассмотрим один из возможных алгоритмов численного решения уравнения (13.19). Разобьем интервал интегрирования [α, β] в (8.19) на N частей ∆ t = (β -α)/N и представим jSm(t) в виде разложения по некоторым базисным функциям φm(t) с неизвестными коэффициентами /т:

Подставляя (8.20) в (8.19) и располагая точки наблюдения (точки коллокации) в серединах интервалов разбиения (τ = τn= α + (n- 1/2) (β -α)/N), приходим к системе линейных алгебраических уравнений (СЛАУ) относительно неизвестных постоянных 1т. Наиболее простой алгоритм получается при кусочно-постоянной аппроксимации искомой функции, когда в качестве базисных берутся функции

182

Численное решение СЛАУ (8.22) может быть получено стандартными методами, например методом Гаусса. В результате решения системы (8.22) находятся значения искомой функции jSm(t) в N -точках коллокации (при t=τn), зная которые можно рассчитать электромагнитное поле в любой точке пространства. Изложенный способ построения численного решения получил название метода саморегуляризации. Более подробно он описан, например в [21].

Отметим, что построение численного решения интегрального уравнения Фредгольма первого рода в общем случае относится к так называемым некорректным задачам. Оно может оказаться неустойчивым: малым изменениям правой части интегрального уравнения могут соответствовать сколь угодно большие изменения решения. В общем случае для построения численного решения интегрального уравнения Фредгольма первого рода требуется использовать так называемые методы регуляризации. Впервые такие методы были разработаны академиком А.Н. Тихоновым. Общие методы регуляризации, изложенные в [19], весьма сложны. В частном случае, когда ядро интегрального уравнения имеет интегрируемую особенность при совпадении аргументов, удается использовать более простые методы решения. Так, благодаря логарифмической особенности ядра K{t,τ) для построения устойчивого решения уравнения (8.19) оказывается возможным использовать описанный выше метод саморегуляризации или несколько более общий метод моментов (см., например, [18]).

8.4. ФИЗИЧЕСКАЯ ОПТИКА (ПРИБЛИЖЕНИЕ ГЮЙГЕНСА-КИРХГОФА)

В 5.7 было показано, что поле в любой точке пространства, внешнего по отношению к некоторой области, ограниченной замкнутой поверхностью S, можно полностью определить по заданным на ней значениям касательных составляющих напряженностей электрического и магнитного полей или, что то же самое, по заданному распределению на S реальных или эквивалентных поверхностных электрических и магнитных токов. Действительно, разбивая мысленно поверхность S на элементарные площадки и рассматривая каждую площадку как элемент Гюйгенса, можно найти полное поле, суммируя поля, созданные отдельными элементами. В качестве такой поверхности часто оказывается удобным выбрать поверхность тела, рассматриваемого в дифракционной задаче.

Если бы на поверхности тела были известны точные значения касательных составляющих векторов Ё и Н, то тем самым были бы найдены точные

значения этих векторов в любой точке пространства. Однако для точного определения составляющих Етτ и Hmτ на поверхности S обычно требуется решить исходную дифракционную задачу. Указанную трудность можно обойти, если ограничиться вычислением приближенных значений составляющих Emτ│s и Hmτ│s на основе некоторых упрощающих предположений. Однако при этом решение соответствующей дифракционной задачи также будет уже не точным, а приближенным. Рассмотрим два примера. Пример 1. Пусть на идеально проводящее тело (рис. 8.4) падает электромагнитная волна, создаваемая в пространстве источником Q. На поверхности тела касательная составляющая вектора Е равна нулю, т.е. на S отсутствуют эквивалентные поверхностные

183

магнитные токи, а текут только поверхностные электрические токи с плотностью. js. Часть поверхности тела (So), которая видна из источника, будем называть освещенной, а остальную часть - теневой. Если линейные размеры l и минимальный радиус кривизны р min освещенной части поверхности велики по сравнению с длиной волны

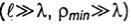то в первом приближении можно пренебречь затеканием токов на теневую сторону тела (т.е. считать, что на ней js = 0) и предположить, что на So плотность тока в каждой точке такая же, какой она была бы при заданном первичном поле на идеально проводящей плоскости, касательной к So в рассматриваемой точке. Эти предположения, конечно, являются приближенными. В действительности при любых конечных размерах тела токи всегда затекают на теневую сторону его поверхности и, кроме того, реальное распределение токов на освещенной стороне несколько отличается от указанного.

Выберем некоторую точку М на So (см. рис. 8.4) и вычислим в ней плотность тока на основе принятых допущений. Предположим, что источник Q находится над идеально проводящей безграничной плоскостью Р, касательной к поверхности S в точке М (рис.

8.5).

Напряженность полного магнитного поля где Н 0 (М)-напряженность первичного магнитного поля, создаваемого источником в точке М,

а Н(М) -напряженность вторичного магнитного поля, обусловленного токами, протекающими по плоскости Р. Напряженность первичного магнитного поля считается известной. Для определения плотности тока в точке М нужно найти в этой точке значение касательной

составляющей вектора Н(n)(М). Из граничного условия (1.110) имеем

где n0-орт внешней нормали к поверхности So в точке М. Для удобства введем локальную декартову систему координат х, у, z (см.

рис. 8.5).

Покажем, что вторичное поле, создаваемое при возбуждении идеально проводящей плоскости Р произвольным первичным полем Ё°,Н°, легко определяется в любой точке пространства из общих физических представлений.

Идеально проводящая плоскость Р полностью экранирует нижнее (z < 0) полупространство от первичного поля. Поэтому должно выполняться соотношение

H(x,y,z) = -H°(x,y,z) при z<0. (8.23)

Любой элемент поверхностного электрического тока, текущего по плоскости Р, создает в точках, расположенных симметрично относительно этой плоскости (например, в точках N1 = N1(х, у, z) и N2= N2(х, у,-z), показанных на рис. 8.5), магнитное поле, касательные составляющие вектора напряженности которого равны по величине и противоположны по направлению, а нормальные составляющие одинаковы. Таким же, свойством будет обладать магнитное поле, созданное всеми токами, текущими по плоскости Р. Следовательно, при z > 0 должны выполняться соотношения

184

Формула (8.26) справедлива и в точке М= М(0,0,0), где z0 = n0. Таким образом, в рассматриваемом приближении на освещенной части поверхности (So) идеально проводящего тела плотность поверхностных электрических токов

а на теневой стороне равна нулю.

Для определения вторичного поля в пространстве, окружающем рассматриваемое тело, можно либо вычислить векторный потенциал

где R - расстояние от элемента dS до точки наблюдения, и затем применить формулы (2.52) и (2.57), либо непосредственно просуммировать поля, создаваемые токами, сосредоточенными в каждом элементе dS, которые можно рассматривать как элементарные электрические вибраторы. С вычислением поля на основе описанной методики для конкретных тел (в частности, для кругового цилиндра) можно ознакомиться, например, в

[17].

Пример 2. Определим электромагнитное поле, проникающее через отверстие So в идеально проводящей плоскости при падении на нее плоской электромагнитной волны:

Пусть рассматриваемая плоскость (экран) расположена в координатной плоскости z = 0 (рис. 8.6). Размеры отверстия будем считать большими по сравнению с длиной волны.

В качестве поверхности интегрирования S выберем плоскость z =+ 0, которая проходит через отверстие So, а вне его совпадает с "теневой" стороной экрана (пунктирная линия на рис. 8.6, а). На экране касательная составляющая вектора Ет равна нулю. При больших по сравнению с длиной волны размерах отверстия можно пренебречь затеканием токов на теневую сторону и, кроме того, приближенно считать, что поле в отверстии совпадает с полем падающей волны, т.е. определяется выражениями (8.29), если в них положить z = 0.

185

Каждый элемент ∆S площади отверстия So

можно рассматривать как элемент Гюйгенса (см. 5.7.2), а при определении поля за отверстием просуммировать.поля, создаваемые каждым элементом ∆S.

Описанный способ решения дифракционных задач известен под названием метода физической оптики. Он принципиально является приближенным, так как распределение токов, по которым вычисляется поле, находится приближенно. Тем не менее при выполнении указанных выше условий метод физической оптики (ФО) удовлетворительно передает структуру поля в области максимальной интенсивности. Метод физической оптики часто называют также приближением Гюйгенса-Кирхгофа.

8.5. ГЕОМЕТРИЧЕСКАЯ ОПТИКА

Одним из наиболее простых методов определения поля, отраженного от больших по сравнению с длиной волны тел, которые имеют достаточно гладкую поверхность, является метод геометрической оптики (ГО). Изложим основные принципы этого метода. Ограничимся случаем, когда рассматриваемое тело является идеально проводящим и расположено в однородной изотропной среде без потерь. Основные идеи ГО изложены во многих книгах (см., например, [23]).

Выше было показано, что направление распространения волны перпендикулярно поверхностям равных фаз. В однородной среде направление распространения плоской волны одинаково во всех точках пространства. Произвольная электромагнитная волна не обладает этим свойством. Однако, на большом расстоянии от источника (по сравнению с длиной волны и размерами источника) поле произвольной электромагнитной волны в достаточно малой области можно представить в виде

где длина волны -в вакууме, е0 и h0-единичные векторы, показывающие ориентацию векторов Ет и Нт соответственно, A и B-медленно меняющиеся функции, зависящие только от поперечных (по отношению к направлению распространения волны) координат, а ф - некоторая вещественная функция координат. Например, в случае плоской волны, распространяющейся вдоль оси Z, функция ф = nz, в

случае сферической волны ф = nr. Здесь - показатель преломления, а εr и μr как обычно, - относительные диэлектрическая и магнитная проницаемости среды, в которой распространяется волна. Функцию ф называют эйконалом. (Термин эйконал, образованный от греческого слова, означающего изображение, был введен для обозначения некоторых связанных функций, но в дальнейшем стал применяться в более широком смысле.) В ГО эйконал имеет смысл оптической длины пути, т.е. пути, учитывающего показатель преломления вдоль луча. Уравнение ф = const определяет поверхности равных фаз. Градиент эйконала (∆ф) представляет собой вектор, перпендикулярный поверхностям равных фаз. Линии этого вектора в геометрической оптике называют лучами. Положительная касательная к лучу в каждой точке совпадает по

186

направлению с вектором Пср = РеП. Поэтому лучи можно рассматривать как линии, вдоль которых происходит распространение энергии. В однородной среде лучи прямолинейны, в неоднородной - криволинейны. При вычислении поля по методу ГО предполагается, что каждой точке луча соответствуют определенные значения векторов Ёт и Нт. Векторы Ет и Нт перпендикулярны лучу, их фазы изменяются линейно вдоль него, а характер изменения амплитуд устанавливается на основе закона сохранения энергии. Как уже отмечалось, в представлении ГО энергия электромагнитного поля распространяется вдоль лучей, соответствующих рассматриваемой волне, которые перпендикулярны поверхностям равных фаз. Поэтому если на какой-либо ПРФ So выделить малую площадку ∆S0, то весь поток энергии, проходящий через нее за период, будет распространяться внутри некоторой трубки, боковая поверхность которой образована лучами, проходящими через контур площадки ∆S0 (рис. 8.7). Такую трубку обычно называют энергетической или силовой. В пределе при ∆S0→0 энергетическая трубка стягивается к одному лучу (N0-N1" на рис. 8.7). Из определения энергетической трубки cледует, что поток энергии через ее боковую поверхность SБ0K отсутствует: на SБОК нормальная к ней составляющая вектора П равна нулю.

Рассмотрим две площадки ∆S0 и ∆S1 вырезаемые энергетической трубкой в поверхностях равных фаз So и S1 соответственно (рис. 8.8). Очевидно, что

средний за период поток энергии через эти площадки должен быть одним и тем же. Следовательно,

187

Где -значения комплексных амплитуд вектора Е в точках Nо и N1 соответственно. Выразим отношение ∆S0/∆S1 через главные радиусы кривизны ρ, и ρ2 поверхности равных фаз

В случае линейной поляризации ориентация векторов Ёт и Нт неизменна вдоль луча. Волны круговой и эллиптической поляризаций можно рассматривать как суперпозицию двух линейно поляризованных волн, поэтому они здесь анализироваться не будут. Таким образом, векторы Ёт(N1)и Ёт(N0) связаны соотношением

Аналогичное соотношение выполняется для векторов Hm (N1) и Hm (N0)

Луч, падающий на поверхность раздела двух сред, расщепляется на отраженный и преломленный. При определенных условиях один из этих лучей (отраженный или преломленный) может отсутствовать. Например, при падении луча на поверхность идеально проводящего тела возникает только отраженный луч. При расчетах по методу ГО предполагается, что так же, как при падении плоской волны на безграничную плоскую границу раздела двух сред, направления отраженного и преломленного лучей определяются законами Снеллиуса, а амплитуды векторов поля, соответствующих отраженному и преломленному лучам, на поверхности раздела двух сред определяются формулами Френеля (см.7.2). Если отражение происходит от поверхности идеально проводящего тела, то нормальная составляющая напряженности электрического поля, соответствующая отраженному лучу, в точке отражения равна нормальной составляющей напряженности электрического поля падающего луча в той же точке, а касательные составляющие напряженности электрического поля падающего и отраженного лучей отличаются только знаком (сдвинуты по фазе на 180°). Иными словами, если в точке отражения М на поверхности идеально проводящего тела комплексная амплитуда

Изменение знака у касательной составляющей показывает, что отражение сопровождается изменением ориентации

вектора относительно ориентации вектора Е°т. При этом направление вектора оказывается перпендикулярным отраженному лучу. Вектор поля отраженного луча в точке М выражается через

соотношением - единичный вектор, направленный по отраженному лучу. Нетрудно показать, что

188

Где l 0 - орт падающего луча в точке MЄS.

Зная поле отраженного луча в точке отражения, можно найти поле в любой точке этого луча. Действительно, рассматривая соответствующую энергетическую трубку, придем к формуле, аналогичной (8.32), в которую, конечно, вместо радиусов кривизны ПРФ падающей волны должны войти радиусы кривизны ПРФ отраженной волны. В тех случаях, когда через рассматриваемую точку пространства проходят несколько лучей (например, падающий и отраженный), поле в этой точке определяется как сумма полей, соответствующих каждому лучу.

Таким образом, для вычисления поля по методу ГО нужно знать главные радиусы кривизны ПРФ падающей и отраженной волн, что является чисто геометрической задачей, которую можно решить в каждом конкретном случае.

В качестве примера рассмотрим в приближении ГО задачу дифракции плоской волны на идеально проводящем круговом цилиндре радиуса а (рис. 8.9), строгое решение которой было получено в (8.2).

Плоскую волну заменим семейством лучей, параллельных оси X, и выделим энергетическую трубку прямоугольного сечения ∆S0=∆y∆z. Сечение трубки плоскостью, перпендикулярной оси Z, показано на рис. 8.9.

Ограничимся вычислением модуля напряженности электрического поля, отраженного от цилиндра, на большом расстоянии от него (т.е. вычислением

Рассмотрим отражение лучей, образующих боковую поверхность выделенной энергетической трубки (два параллельных луча на рис. 8.9). Первый луч отражается в точке М1 которая видна из начала координат под углом 0. Соответствующий отраженный луч составляет с осью X угол 20. Второй луч отражается в точке М2, которая видна из начала координат под углом θ + ∆θ. Соответствующий отраженный луч составляет с осью X угол 2 (θ + ∆θ). Таким образом, пучок лучей, образующий энергетическую трубку, после отражения от цилиндра становится расходящимся. Поперечное сечение трубки, соответствующей отраженной волне

, где r1- расстояние от точки O1 до рассматриваемого сечения ∆S1 Учитывая, что ∆y = a cos θAθ, получаем из формулы (8.30) следующее соотношение:

189

Зависимость величины от угла φ (функция 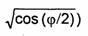)показана пунктирной линией на рис. 8.2. Из приведенных на этом рисунке графиков следует, что различие между результатами, полученными методом ГО, и строгим решением в освещенной области уменьшается с увеличением kа = 2πа/λ.

Как уже отмечалось, метод геометрической оптики является приближенным. Он позволяет определить отраженное поле, если радиусы кривизны ПРФ падающей и отраженной волн велики по сравнению с длиной волны. При этом необходимо, чтобы размеры отражающего тела и минимальный радиус кривизны его поверхности были велики по сравнению с λ, а источник, создающий электромагнитное поле, находился на достаточно большом расстоянии d от поверхности тела (kd>> 1). Получаемые в этом случае результаты будут близки к точным в освещенной части пространства в точках, достаточно удаленных от границы геометрической тени. Для определения поля в области геометрической тени, а также вблизи точек, в которых пересекается семейство отраженных лучей (такие точки называют фокальными), и вблизи огибающих семейства лучей (их называют каустиками) метод геометрической оптики неприменим. Например, согласно представлениям геометрической оптики в области геометрической тени поле должно отсутствовать. В действительности, из-за дифракции волн поле проникает в область геометрической тени (см., например, диаграммы на рис. 8.2).

Методы вычисления поля, основанные на приближении Гюйгенса-Кирхгофа (метод физической оптики) и на геометрической оптике, существенно различны. В ГО предполагается, что поле в любой точке пространства определяется значениями его векторов в тех точках поверхности тела или поверхности равных фаз (волновой поверхности), из которых приходят лучи в данную точку. Метод физической оптики использует принцип Гюйгенса. Однако эти методы имеют общую черту. В ГО предполагается, что в каждой точке поверхности идеально проводящего тела волна отражается так же, как от идеально проводящей плоскости, касательной к поверхности тела в рассматриваемой точке. Поэтому выражая вектор плотности поверхностных токов js через напряженность полного магнитного поля, вычисленного на основе ГО, получаем, что на освещенной части поверхности тела выполняется соотношение (8.27), которое лежит в основе приближения Гюйгенса-Кирхгофа. Следовательно, в методе, основанном на приближении Гюйгенса-Кирхгофа по существу предполагается, что вблизи отражающего тела справедливы законы геометрической оптики. Поэтому, как уже отмечалось, приближение Гюйгенса-Кирхгофа и называют методом физической оптики. Часто методы ГО и ФО совмещают. Например, при расчете диаграмм направленности параболических (и ряда других) антенн вначале на основе геометрической оптики определяют поле в раскрыве антенны, а затем по найденным значениям векторов Ёт и Нт вычисляют поле в дальней зоне, используя приближение Гюйгенса-Кирхгофа.

8.6. МЕТОД КРАЕВЫХ ВОЛН

Метод краевых волн в физической теории дифракции, предложенный П. Я. Уфимцевым, является развитием и уточнением метода физической оптики применительно к выпуклым

190