Пименов Ю.В., Муравцов А.Д. Техническая электродинамика, 2000

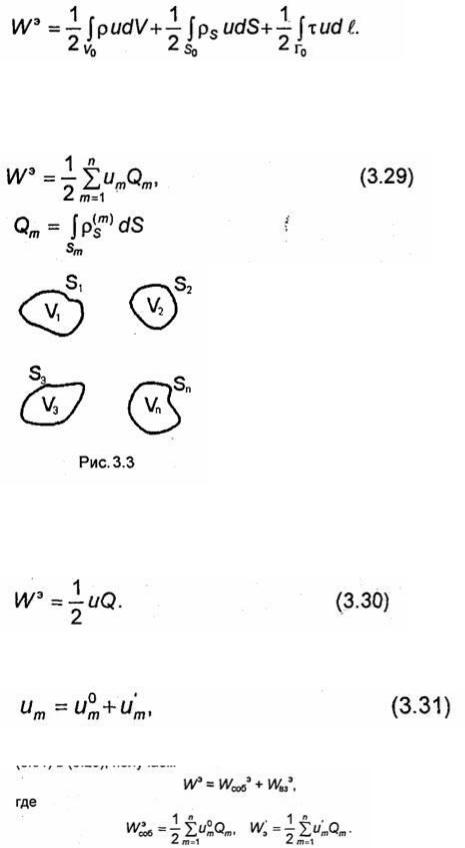
Рассмотрим частный случай, когда электростатическое поле создается зарядами, расположенными на проводниках. Пусть имеется п проводников (рис. 3.3), потенциалы которых равны соответственно u1, и2.....ип. Так как потенциал проводника имеет одинаковые значения во всех его точках, а заряды распределены по его поверхности, то, применяя формулу (3.27), получаем

-полный заряд m-гo проводника, a p(sm)-плотность поверхностных зарядов, с которой заряд Qm распределен по поверхности Sm рассматриваемого проводника.

Выражение для энергии уединенного проводника, т.е. бесконечно удаленного от других тел и зарядов, находится из формулы (3.29) как частный случай. Полагая в (3.29) п = 1, получаем

На энергию электростатического поля не распространяется принцип суперпозиции. Поэтому энергия системы проводников не равна суммарной энергии уединенных проводников. Представим потенциал m-го проводника в виде суммы:

где ит° - потенциал уединенного проводника, а ит- потенциал, создаваемый действием всех остальных проводников. Подставляя (3.31) в (3.29), получаем

Величину 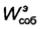принято называть собственной энергией системы проводников, а 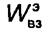- взаимной энергией.

Можно показать, что заряды, находящиеся на системе заданных проводников, расположенных в диэлектрике, распределяются по поверхности этих проводников таким

81

образом, что энергия получающегося в результате электростатического поля минимальна. Это важное утверждение известно под названием теоремы Томсона.

3.4. ЕМКОСТЬ

Потенциал уединенного проводника зависит от его размеров и формы, а также от величины имеющегося на нем заряда. При равных потенциалах уединенные тела разной формы или размеров обладают зарядами разнойвеличины. Отношение величины заряда к потенциалу при условии, что потенциалы бесконечно удаленных точек считаются равными нулю, называется емкостью уединенного проводника:

С = Q/u. (3.32)

Емкость измеряют в фарадах (Ф = Кл/В). С учетом формулы (3.32) выражение для энергии электростатического поля уединенного заряженного проводника (3.30) принимает вид

W3 = Си2/2 = Q2/2C. (3.33)

Если проводник не уединен, то потенциал, приобретаемый им при сообщении ему какоголибо заряда, существенно зависит от формы и расположения других проводников. Заряженные тела создают электрическое поле, под действием которого заряды на всех соседних проводящих телах перераспределяются. Перераспределение продолжается до тех пор, пока суммарное электрическое поле внутри каждого проводника не станет равным нулю.

Рассмотрим систему из n проводников с зарядами Q1, Q2.....Qn соответственно. Потенциал каждого проводника линейно

зависит от величины зарядов Q1, Q2.....Qn, т.е. должно выполняться л соотношений вида

где ит - потенциал m-го проводника, a amk, k = 1, 2,..., n- некоторые постоянные, называемые потенциальными коэффициентами, зависящие от размеров, формы и взаимного расположения проводников. Коэффициент атk численно равен потенциалу л7го проводника, наведенному зарядом k-го проводника при условии, что заряд последнего равен 1 Кл. а заряды остальных - нулю. Например, a13 численно равен потенциалу проводника 1, наведенному единичным зарядом проводника 3 при отсутствии зарядов на остальных проводниках.

Система уравнений (3.34) определяет потенциалы проводников через заряды Q и потенциальные коэффициенты атк. Если потенциалы и1, и2.....ип проводников и потенциальные коэффициенты атk известны, то система (3.34) позволяет однозначно определить заряды проводников

Постоянные коэффициенты стk, т= 1, 2,..., п; k= 1, 2,....n однозначно определяются потенциальными коэффициентами aip, i=1,2,..., n; р = 1, 2,..., n, и находятся при решении системы (3.34) относительно зарядов Q1, Q2....,Qn. Из уравнений (3.35) следует, что коэффициент стk численно равен заряду m-го проводника, если потенциал k-го проводника равен единице, а потенциалы остальных проводников - нулю.

Отметим, что потенциальные коэффициенты атk и коэффициенты стk удовлетворяют правилу взаимности:

Обычно систему уравнений (3.35) записывают в несколько иной форме. Прибавим к правой части m-го уравнения системы равное нулю выражение

В результате получим следующую систему п

уравнений:

82

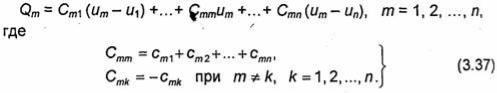
Коэффициенты Стk называют частичными емкостями. Иногда вводят различные названия для коэффициентов с одинаковыми и разными индексами: коэффициент Стт называют собственной емкостью т-го проводника, а Стk - взаимной емкостью m-го и k-го проводников. Отметим, что собственные емкости уединенных проводников могут отличаться от коэффициентов Стт. Аналогично взаимные емкости двух проводников, отделенных от остальных, могут отличаться от соответствующих коэффициентов Стk, так как частичные емкости Стk и Стт определяются не только рассматриваемыми проводниками, но и всеми остальными проводниками системы.

Из формул (3.36) и (3.37) следует, что частичные емкости также удовлетворяют правилу

взаимности: Стk = Сkт.

3.5. ПОСТАНОВКА И МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЭЛЕКТРОСТАТИКИ 3.5.1. Определение поля, создаваемого известными источниками в безграничной однородной среде

Прямая задача электростатики заключается в определении векторов поля по заданному распределению зарядов. При этом область пространства, в которой требуется определить поле, может быть как ограниченной, так и неограниченной.

Наиболее просто такая задача решается в том случае, когда рассматриваемая область представляет собой неограниченное пространство, заполненное однородной изотропной средой, а заряды сосредоточены внутри некоторого объема конечных размеров (т.е. отсутствуют заряды в бесконечно удаленных точках). Математически она формулируется следующим образом. Задана объемная плотность заряда ρ как функция координат. Требуется найти функцию и, удовлетворяющую уравнению Пуассона (3.7) и обращающуюся в нуль в бесконечно удаленных точках. Эта задача была рассмотрена в 2.5.2 и 3.2. Ее решением является выражение (3.9). Если заряды распределены на поверхности конечных размеров S с плотностью ρs, то соответствующий им потенциал определяется формулой (3.10). Если же поле создается зарядами, распределенными с линейной плотностью τ вдоль контура конечных размеров Г, искомая функция и определяется выражением (3.11).

В тех случаях, когда система зарядов не может быть охвачена описанной вокруг начала координат сферой конечного радиуса, т.е. содержит заряды в бесконечно удаленных точках (например, бесконечно длинная заряженная нить), то формулы (3.9)—(3.11) могут оказаться непригодными. Это, в частности, имеет место при решении так называемых плоских задач электростатики, т.е. при одинаковом распределении зарядов (и поля) в любой плоскости, перпендикулярной к некоторой прямой линии, например к одной из осей декартовой системы координат. Такую систему зарядов можно представить как бы состоящей из тонких, равномерно заряженных по длине бесконечно протяженных прямолинейных нитей. Поэтому для определения поля, создаваемого подобной системой зарядов, нужно знать потенциал, создаваемый одной нитью.

Пусть имеется бесконечно тонкая равномерно заряженная с плотностью τ = const нить. Введем цилиндрическую систему координат τ, φ, z, ось Z которой совпадает с нитью, и рассмотрим поток вектора D через поверхность кругового цилиндра радиуса а и длиной l, ось которого совпадает с осью Z (рис. 3.4). Из условия задачи очевидно, что поле должно обладать осевой симметрией, а векторы Е и D должны быть перпендикулярны к боковой поверхности цилиндра. Поэтому поток вектора D через основания цилиндра отсутствует, а поток через боковую поверхность равен D·2πrΔl. Используя теорему Гаусса (1.40) и учитывая, что полный заряд внутри рассматриваемого цилиндра равен τΔl,

получаем

83

где r0-орт радиуса-вектора цилиндрической системы координат. Поскольку в рассматриваемом случае поле не зависит от переменных φ и z (производные потенциала и по переменным φ и z равны нулю), то из определения электростатического потенциала (3.2) и формулы (3.38) имеем

где В - произвольная постоянная. Обычно постоянную В полагают равной нулю и потенциал нити определяют выражением

Если вместо нити имеется тонкий бесконечно длинный цилиндр с площадью поперечного сечения ΔS, равномерно заряженный с объемной плотностью ρ, то соотношение (3.39) примет вид

где - расстояние от элемента ΔS, характеризуемого координатами ζ£, η, до точки N с координатами х, у, в которой вычисляется потенциал.

От формулы (3.41) нетрудно перейти к выражению для потенциала, созданного произвольным двумерным (не зависящим от z) распределением зарядов с плотностью ρ:

где S - площадь сечения данной системы зарядов плоскостью, перпендикулярной к оси Z

(рис. 3.5).

Функцию и, определяемую соотношениями (3.39)-(3.42), принято называть логарифмическим потенциалом.

Если поле создается зарядами, распределенными по цилиндрической поверхности S, образующие которой параллельны оси Z, а плотность поверхностных зарядов не зависит от переменной z, то соответствующий логарифмический потенциал

84

где Г-линия пересечения поверхности S с плоскостью, перпендикулярной оси, Z, a R - расстояние от элемента dl до точки N, в которой вычисляется потенциал (рис. 2.9).

Из формул (3.39)-(3.43) следует, что логарифмический потенциал на бесконечности нельзя принять равным нулю не только в направлении оси Z, но и в перпендикулярных к ней плоскостях. Исключение составляет случай, когда полный заряд системы равен нулю.

Поле, соответствующее потенциалам (3.42) и (3.43), убывает на бесконечности пропорционально 1/r (или быстрее), если поверхность S (или контур Г) ограничена. Если S (или Г) не ограничена, то векторы Е и D на бесконечности могут иметь конечные значения (например, поле равномерно заряженной плоскости).

3.5.2. Примеры определения поля известных источников

В некоторых задачах напряженность электростатического поля, сoдаваемого в безграничной однородной изотропной среде заданным распределением зарядов, легко находится непосредственно без предварительного вычисления электростатического потенциала и, в других - введение потенциала и упрощает построение решения. Рассмотрим несколько примеров.

Поле равномерно заряженной сферы. Пусть заряд Q равномерно распределен по поверхности сферы радиуса а, находящейся в однородной изотропной безграничной среде с диэлектрической проницаемостью ε. Введем сферическую систему координат r, θ, φ, начало которой совпадает с центром сферы. Из симметрии задачи очевидно, что поле в этом случае может зависеть только от координаты r, причем векторы Е и D могут иметь только радиальную компоненту. Применяя закон Гаусса (1.40) к сфере радиуса r и учитывая, что заряды равномерно распределены по поверхности сферы радиуса а, получаем

Отсюда следует, что поле равномерно заряженной сферы в области r≥a совпадает с полем точечного заряда величины q= Q, расположенного в начале координат. Электростатический потенциал в этом случае определяется выражениями:

Из определения емкости и формулы (3.44) находим

Поле равномерно заряженного цилиндра. Пусть заряд равномерно распределен по объему бесконечного кругового цилиндра радиуса а с плотностью ρ = const. Из соображений симметрии очевидно, что векторы Е и D в этом случае будут направлены перпендикулярно оси цилиндра. Рассмотрим поток вектора D через поверхность цилиндра длиной l и радиуса а, ось которого совпадает с осью основного цилиндра. Учитывая, что поток вектора D через основания этого цилиндра равен нулю, из закона Гаусса (1.40) получаем

85

где r0 - координатный орт переменной r цилиндрической системы координат.

Если заряд распределен по бесконечно протяженной цилиндрической поверхности радиуса а с плотностью поверхностных зарядов ps = const, то

Отметим, что поля, создаваемые равномерно заряженными бесконечно протяженными цилиндром и цилиндрической поверхностью радиуса а в области r≥a совпадают с полем равномерно заряженной нити с линейной плотностью зарядов τ =πа2ρ и τ = 2πaρs соответственно.

Поле электростатического диполя. Электростатическим диполем называется система из двух близлежащих равных по величине постоянных точечных разноименных зарядов +q и -q (рис. 3.6). Диполи характеризуются дипольным моментом

где l- вектор, направленный от отрицательного заряда к положительному, по абсолютной величине равный расстоянию между зарядами l, а 10- орт, соответствующий вектору l(l=lol).

Если сближать заряды, одновременно увеличивая их значения так, чтобы вектор р оставался неизменным, то в пределе получится точечный или идеальный диполь с тем же моментом.

Вычислим поле электростатического диполя. Введем сферическую систему координат r, θ, φ так, чтобы полярная ось проходила через оба заряда, а начало координат находилось на равном расстоянии от них (рис. 3.6). Потенциал, создаваемый диполем, найдем

86

по принципу суперпозиции как сумму потенциалов, создаваемых зарядами +q и-q:

где R1 и R2 - расстояния соответственно от зарядов +q и -q до точки, в которой вычисляется потенциал (рис. 3.7):

При вычислении поля будем считать, что расстояние r от центра диполя до точки наблюдения велико по сравнению с расстоянием между зарядами l. При этом условии справедливы следующие приближенные равенства

При этом (3.46) принимает вид

где rо - координатный орт переменной г. Для определения напряженности электрического поля воспользуемся соотношением (3.2). Выражение для grad и в сферической системе координат приведено в приложении (см. (П. 15)). Выполняя указанные в (П. 15) действия и учитывая, что в рассматриваемом случае ди/дφ = 0, получаем

Направления единичных векторов r0,θ0 и φ0 показаны на рис. 3.6. Как видно, вектор напряженности электрического поля, создаваемого электростатическим диполем, не зависит от угла φ (поле обладает осевой симметрией) и имеет две составляющие:

Силовые линии этого поля показаны на рис. 3.8.

Поле параллельных противоположно заряженных нитей.

Вычислим поле двух параллельных бесконечно тонких равномерно заряженных нитей с линейной плотностью зарядов +τ и -τ соответственно, расположенных на расстоянии 2£ друг от друга (рис. 3.9). Введем декартову х, у, z систему координат, как показано на рис. 3.9. Потенциал системы нитей равен сумме потенциалов каждой и| них. Потенциал одной нити определяется формулой (3.39). Выбирая постоянную В так, чтобы на оси Z потенциал и был равен нулю, получаем

87

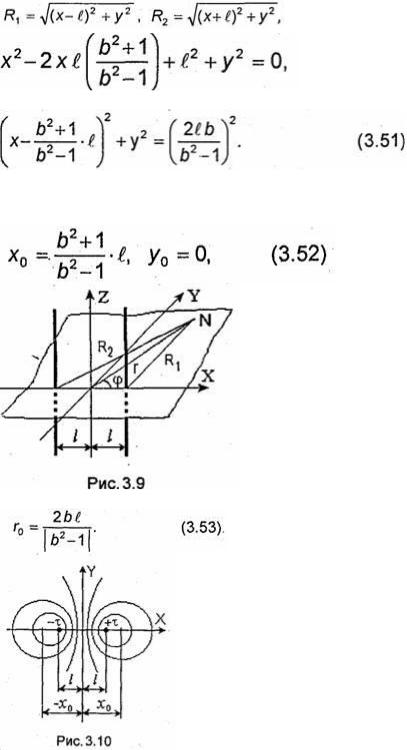
где R1 и R2 - расстояния от положительно и отрицательно заряженных нитей соответственно до точки N, в которой вычисляется потенциал (рис. 3.9).

Найдем эквипотенциальные поверхности рассматриваемой системы зарядов. Потенциал (3.49) постоянен, если

R2/R1 = b = const. (3.50)

Следовательно, эквипотенциальные поверхности представляют собой поверхности круговых цилиндров, параллельных оси Z.Найдем их радиусы и положение осей. Так как

, то из уравнения (3.50) следует соотношение

которое можно переписать в виде

Уравнение (3.51) описывает семейство окружностей, образующихся при пересечении эквипотенциальных поверхностей с плоскостью XOY. Центры окружностей расположены на оси Х и имеют координаты:

а их радиусы равны

Значения параметра b у окружностей, расположенных симметрично относительно оси Y, выражаются обратными числами (например, Ьо и 1/Ь0). Величины r0, l и х0 связаны простым соотношением

88

являющимся следствием формул (3.52) и (3.53). Решая уравнение (3.53) относительно b и используя равенства (3.52) и (3.54), находим значения параметра b и потенциала и на соответствующей эквипотенциальной поверхности:

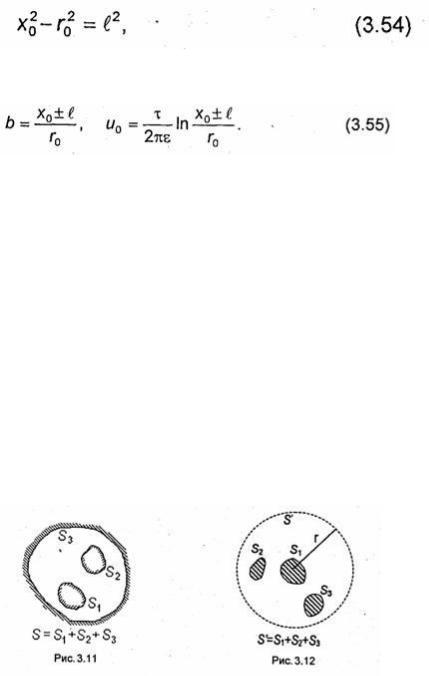
В формулах (3.55) знак "+" выбирают для точек, находящихся справа от оси У, а знак "-" для точек, лежащих слева от оси У. Структура эквипотенциальных поверхностей показана на рис. 3.10.

3.5.3. Краевые задачи электростатики

Выше был рассмотрен вопрос об определении поля в однородном изотропном пространстве по известному распределению зарядов. Однако на практике часто встречаются задачи другого типа, например: задано расположение и форма всех проводников, находящихся в однородном диэлектрике, требуется найти поле в этом диэлектрике, если известен потенциал каждого проводника (задача 1) или общий заряд каждого проводника (задача 2). Такие задачи называют краевыми задачами электростатики.

Область V, в которой требуется найти поле, либо ограничена поверхностями проводников (рис. 3.11), либо простирается до бесконечности. Во втором случае проводящие тела целиком лежат внутри области V (рис. 3.12). Потенциал в бесконечно удаленных точках считается равным нулю.

Доказано (см., например, [12]), что данные задачи имеют единственное решение. В задаче 1 и вектор Е электростатического поля и потенциал и определяются однозначно. Различные решения задачи 2 могут отличаться на постоянную величину в выражениях для электростатического потенциала. Однако это различие

несущественно при вычислении вектора Е. В задачах смешанного типа, когда на какомлибо проводнике (или нескольких проводниках) задан потенциал, а для других известен полный заряд, функция и определяется однозначно.

Отметим, что построение строгого аналитического решения краевой задачи электростатики во многих случаях сопряжено со значительными математическими трудностями. Практически его удается найти лишь при достаточно простой форме проводящих тел. Подробное изложение методов решения задач электростатики имеется в

[15 и 16].

Рассмотрим несколько примеров с целью дать представление о некоторых методах решения задач электростатики.

Электростатическое поле двухпроводной линии. Вычислим электростатическое поле двухпроводной линии, т.е. поле двух параллельных противоположно заряженных бесконечных цилиндров (проводов) радиуса а, расстояние между осями которых равно 2Л (рис. 3.13). Потенциал одного из проводов равен -U, другого - соответственно +U. Заряды проводов на единицу длины равны по величине и противоположны по знаку.

89

Математически задачу можно сформулировать следующим образом. Требуется найти функцию и, которая во внешнем по отношению к цилиндрам пространстве удовлетворяет уравнению Лапласа (3.8), на поверхностях цилиндров принимает заданные

значения +U и -U, а в направлениях, перпендикулярных осям цилиндров, на бесконечности обращается в нуль. В силу теоремы единственности существует только одна функция и, удовлетворяющая указанным требованиям. Для построения функции и применим искусственный прием.

Выше было показано, что эквипотенциальные поверхности поля двух параллельных противоположно заряженных нитей образуют семейство поверхностей круговых цилиндров. Найдем расстояние между нитями, при котором две эквипотенциальные поверхности будут совпадать с поверхностями цилиндров, образующих двухпроводную линию. Полагая в (3.54) хо = h и rо = а, получаем

Потребуем, кроме того, чтобы потенциалы рассматриваемых цилиндров, расположенных справа и слева от оси Y (рис. 3.13), равнялись +U и -U соответственно. Подставляя хо = h в формулу (3.55) и учитывая соотношение (3.56), определяем линейную плотность зарядов эквивалентных нитей:

Таким образом, определены и местоположение (х = ± h, у = 0), и плотности линейных зарядов (±τ) эквивалентных заряженных нитей (их называют электрическими осями проводов). Потенциал этих нитей, определяемый выражением (3.49), во внешнем по отношению к проводам линии пространстве отвечает всем поставленным требованиям, т.е. является решением задачи. Вектор Е вычисляется по формуле Е =- grad и.

Подчеркнем, что потенциал найденных таким образом эквивалентных заряженных нитей (электрических осей проводов) совпадает с искомым потенциалом только вне цилиндров, образующих двухпроводную линию. Внутри цилиндров истинный потенциал имеет постоянные значения (±U т.е. принципиально отличается от определяемого выражением

(3.49).

Определим емкость С1 на единицу длины рассматриваемой системы проводов как отношение заряда, приходящегося на единицу длины одного из проводов, к разности потенциалов между проводами:

Из (3.57) и (3.58) получаем

90