Пименов Ю.В., Муравцов А.Д. Техническая электродинамика, 2000

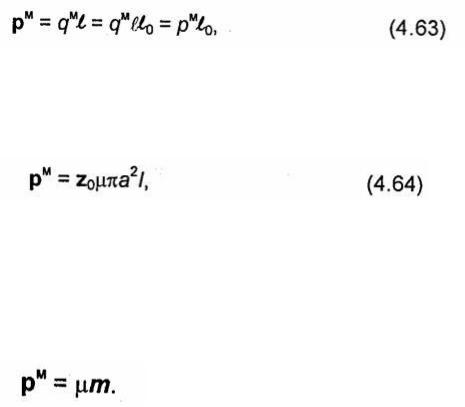
магнитостатическим. С каждой магнитостатической задачей можно сопоставить некоторую электростатическую задачу, переход к которой может быть осуществлен, например, на основе принципа двойственности (см. 2.6). Заменим в формуле (4.62) Н на Е, μ на-ε, а рм-на (-р), где p = ql- величина момента некоторого электростатического диполя системы двух зарядов q и -q, расположенных на расстоянии l. После этих преобразований формула (4.62) будет полностью совпадать с выражением (3.47) для напряженности электрического поля, создаваемого электростатическим диполем с моментом p = zop. Следовательно, выражение (4.62) является магнитостатическим аналогом формулы (3.47). По аналогии с электростатическим диполем можно ввести понятие о магнитном диполе (т.е. о системе двух точечных магнитных зарядов +qM и -qM, расположенных на расстоянии l друг от друга), поле которого определяется выражением (4.62). При этом будет выполняться соотношение pM = qMl. Момент магнитного диполя, как и момент электрического диполя р, является векторной величиной:

где l -вектор, направленный от отрицательного магнитного заряда (-qM) к положительному (+qM), по абсолютной величине равный расстоянию между зарядами l, a l0-орт вектора l. Соотношение (4.62) было получено из выражения (4.59) для магнитного поля кругового витка (рамки) с током. Следовательно, рамка с током /, расположенная в плоскости z = 0 симметрично относительно оси Z, создает на больших по сравнению с его радиусом расстояниях такое же поле, как магнитный диполь с моментом

помещенный в начале координат. Выражение (4.64) можно представить в виде

(4.65)

где S-площадь рамки, а n0-орт нормали к плоскости рамки (рис. 1.3).

Соотношение (4.65) справедливо для плоских рамок произвольной формы. Отметим, что вектор рм связан с введенным ранее (см. 1.2) магнитным моментом рамки т соотношением

4.7. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ПОСТОЯННОГО ТОКА Электрическое поле в диэлектрике, окружающем проводники с постоянным током.

Постоянный ток помимо магнитного поля создает также электрическое поле, которое описывается системой уравнений (1.576). Следовательно, оно является потенциальным, и для его характеристики можно ввести скалярный потенциал и, связанный с вектором Е соотношением (3.2). Если рассматриваемая среда является однородной (ε = const) и в ней отсутствуют свободные заряды (ρ = 0), то потенциал и удовлетворяет уравнению Лапласа (3.8), а система уравнений (1.576) принимает вид

rot Е = 0, div D = О, D = εE.

Как видно, уравнения, описывающие электрическое поле постоянного тока в идеальном диэлектрике, окружающем проводники, совпадают с уравнениями, описывающими электростатическое поле. Однако электрическое поле постоянного тока отличается от электростатического. Электрическое поле постоянного тока существует и в проводящей среде. Вектор Е связан с вектором плотности тока проводимости соотношением j = σE. Это приводит к изменению граничных условий на поверхности проводника по сравнению с граничными условиями в случае электростатики. Так как электрический ток в проводнике создает падение потенциала, то поверхность проводника уже не будет

111

эквипотенциальной и на ней появится отличная от нуля касательная составляющая напряженности электрического поля. При определении поля в диэлектрике, окружающем проводники с постоянными токами, это в большинстве случаев несущественно, так как касательная составляющая вектора Е пренебрежимо мала по сравнению с нормальной составляющей.

Рассмотрим в качестве примера соотношение между нормальной и касательной составляющими вектора Е в воздухе у поверхности проводов двухпроводной линии передачи (см. рис.4.7). Пусть проводники расположены на расстоянии 2h = 10 см друг от друга при разности потенциалов между ними в 200 В и плотностью тока j=2А/мм2. Проводники предполагаются выполненными из меди (σ = 5,65-107 См/м). Касательную составляющую вектора Е определим из закона Ома: Еτ =j/σ = 0,035 В/м. Для оценки величины нормальной составляющей найдем отношение разности потенциалов между проводами к расстоянию 2/7 между ними: ∆u/(2h) = 2000 В/м. В действительности поле между проводами является неоднородным, причем наиболее сильное поле сосредоточено около проводов, поэтому истинное значение Еп будет больше ∆u(2h). Отношение Еn к Еτ, таким образом, даже для рассматриваемого случая линии низкого напряжения имеет порядок 105. Это позволяет в большинстве практически интересных случаев при вычислении электрического поля в диэлектрике, окружающем проводники с постоянными токами, пренебречь касательной составляющей, т.е. Читать, что граничные условия являются такими же, как в электростатике, и для определения поля использовать решения соответствующих электростатических задач.

Электрическое поле в проводящей среде. Если в рассматриваемой области отсутствуют сторонние эдс, то электрическое поле постоянного тока в проводящей среде описывается следующей системой дифференциальных уравнений:

rotE = 0, j = aE, div j = 0. (4.66)

Соответствующие интегральные соотношения имеют вид

Второе уравнение системы (4.67) является следствием закона сохранения заряда (1.50), так как в случае стационарного электромагнитного поля dQ/dt=O. Из этого уравнения следует, что на грайице раздела двух сред с различными удельными проводи-мостями нормальная составляющая вектора j является непрерывной:

а касательные составляющие связаны соотношением

Равенство (4.68) выводится так же, как граничное условие для нормальной составляющей вектора В (см. 1.7.1), а формула (4.69) является следствием соотношения Е1τ = Е2τ.

В ряде практически важных случаев требуется найти токи, которые возникают в среде, изолирующей проводники друг от друга (токи утечки). Удельная проводимость изоляции во много раз меньше удельной проводимости металла. Поэтому вектор плотности тока утечки можно считать перпендикулярным к поверхности проводников. Действительно, пусть угол между вектором j и нормалью к поверхности раздела в первой среде (в изоляции) равен θ1 а во второй (в металле) -θ2. Из равенства (4.68) и (4.69) получается следующее соотношение между углами θ1 и θ2:

Так как отношение σ1 /σ2 очень мало (например, для кабельной бумаги и меди оно равно около 1,7∙10-21), угол θ1 можно считать равным нулю при любом угле 92.

112

Аналогия между электрическим полем постоянного тока и электростатическим полем. Из уравнений (4.66) следует, что электрическое поле постоянного тока является потенциальным, т.е. вектор Е можно представить в виде E=-grad u. В случае однородной проводящей среды (а = const) условие divj = O эквивалентно условию divE = 0. Следовательно, в однородной проводящей среде потенциал и электрического поля постоянного тока в области, в которой отсутствуют сторонние эдс, удовлетворяет уравнению Лапласа (divE=-div grad u = 0, т.е. ∆2u = 0). Если на границе рассматриваемой области значения потенциала и известны, то задача определения электрического поля постоянного тока в однородной проводящей среде сводится к нахождению потенциала и, удовлетворяющего уравнению Лапласа V2u = 0 и заданным граничным условиям. К такой же задаче сводится задача определения электростатического поля в однородном диэлектрике, когда внутри рассматриваемой области отсутствуют заряды. Как известно, такая задача имеет единственное решение. Следовательно, электрическое поле постоянного тока в однородной проводящей среде аналогично электростатическому полю в однородном диэлектрике, если конфигурация рассматриваемых областей в обоих случаях одинакова и, кроме того, одинаковы граничные условия для потенциалов. Эта аналогия позволяет использовать известные решения электростатических задач для нахождения электрического поля постоянного тока и наоборот.

В качестве примера применения указанной аналогии вычислим сопротивление R между электродами, находящимися в однородной проводящей среде. Пусть потенциалы электродов равны U1 и U2, причем U1>U2. Согласно закону Ома R=(U1-U2)/I, где /-ток

между электродами. Очевидно, что , где S-замкнутая поверхность, охватывающая один из электродов. Учитывая, что j = σE, получаем

Для определения величины рассмотрим другую задачу.

Пусть такие же электроды находятся в однородном идеальном диэлектрике, характеризуемом диэлектрической проницаемостью ε. Поток вектора Е через поверхность S при этом согласно закону Гаусса равен

где Q-заряд электрода, находящегося внутри поверхности S.

Если потенциалы электродов в этом случае также равны U1 и U2, то на основе указанной

аналогии можно утверждать, что интеграл в формулах (4.70) и (4.71) имеет одно и то же значение. Так как из определения емкости С системы двух проводников (см. формулу (3.72)) следует, что Q = C| U1 -U2, то

Подставляя (4.72) в (4.70), получаем

Используем формулу (4.73) для определения сопротивления утечки изоляции коаксиального кабеля. Емкость на единицу длины коаксиального кабеля или, что то же самое, емкость на единицу длины цилиндрического конденсатора (рис. 3.21) определяется выражением (3.76). Подставляя (3.76) в (4.73), находим, что сопротивление утечки на единицу длины коаксиального кабеля

113

где σ-удельная проводимость изоляции кабеля; a1- радиус внутреннего провода кабеля; а2- внутренний радиус оболочки кабеля (рис. 4.4).

114

Глава 5 ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН 5.1. ВВЕДЕНИЕ

Возможность излучения и распространения электромагнитной энергии в пространстве, по существу, непосредственно следует из положения Максвелла, согласно которому электрический ток может циркулировать в диэлектрике и свободном пространстве в виде тока смещения. При этом ток смещения, как и ток проводимости, создает вокруг себя магнитное поле. Своим предположением, основанным на опытах Фарадея, Максвелл как бы приписал диэлектрику и свободному пространству свойства проводника - проводника тока смещения. Так как электромагнитное поле является носителем электромагнитной энергии, то распространение в пространстве токов смещения сопровождается возникновением активного потока энергии (мощности излучения), распространяющегося от источника, создающего токи смещения, в окружающее пространство. Принципиальная возможность ответвления (излучения) электромагнитной энергии в пространство доказывается теоремой Пойнтинга (см. 1.8), являющейся прямым следствием уравнений Максвелла.

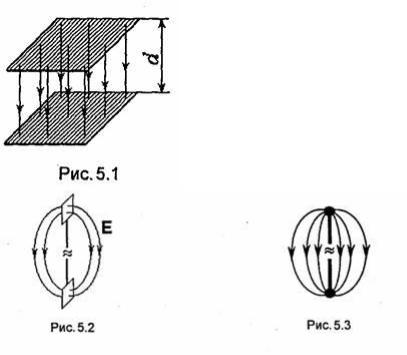
Таким образом, любая электрическая схема, способная создавать в пространстве токи смещения, является излучателем электромагнитной энергии или, как принято говорить, излучателем электромагнитных волн. Рассмотрим, например, конденсатор, питаемый источником переменной ЭДС (рис. 5.1). В пространстве между обкладками конденсатора циркулирует ток смещения. Так как пространство, окружающее конденсатор, обладает способностью проводить ток смещения, то последний должен ответвляться в него так же, как ответвлялся бы ток проводимости, если бы конденсатор находился в пространстве, обладающем проводимостью. Процесс ответвления токов смещения и, следовательно, излучения электромагнитной энергии в пространство, окружающее конденсатор, является с точки зрения теории Максвелла таким

ким же естественным, как и процесс ответвления энергии в провода, присоединенные к какому-либо источнику эдс.

Практически в качестве излучателей электромагнитных волн (антенн) применяют схемы, удовлетворяющие определенным требованиям. Обычно стремятся уменьшить реактивную мощность, непосредственно связанную с антенной и не излучаемую в пространство. Показанная на рис. 5.1 схема излучателя в виде уединенного конденсатора из двух параллельных пластин в указанном смысле является неудачной. В этой схеме

115

электромагнитное поле сосредоточено в основном в пространстве между пластинами, что приводит к большой реактивной мощности по сравнению с мощностью излучения. Реактивная мощность уменьшается при повороте пластин конденсатора и расположении их так, как показано на рис. 5.2.

Один из вариантов схемы, обеспечивающей интенсивное излучение, показан на рис. 5.3. Эта схема, в которой пластины заменены проводами с шарами на концах, была впервые осуществлена Генрихом Герцем и известна под названием диполя Герца.

Инициатива и практическое решение вопроса применения радиоволн в качестве средства связи принадлежит А.С. Попову, который впервые в мире осуществил сеанс радиосвязи. Им же были предложены и осуществлены передающие и приемные антенны в виде несимметричных вибраторов.

5.2. ЭЛЕМЕНТАРНЫЙ ЭЛЕКТРИЧЕСКИЙ ВИБРАТОР

Элементарным электрическим вибратором (ЭЭВ) называют короткий по сравнению с длиной волны провод, обтекаемый электрическим током, амплитуда и фаза которого не изменяются вдоль провода. Этот вибратор является по существу идеализированной, удобной для анализа излучающей системой, так как практически создание вибратора с неизменными по всей длине амплитудой и фазой тока невозможно. Однако вибратор Герца (рис. 5.3) оказывается весьма близким по своим свойствам к ЭЭВ.

Благодаря имеющимся на его концах металлическим шарам, которые обладают значительной емкостью, амплитуда тока слабо изменяется вдоль вибратора. Неизменность фазы обеспечивается малыми по сравнению с длиной волны размерами вибратора.

Изучение поля ЭЭВ крайне важно для понимания процесса излучения электромагнитных волн антеннами. Любое проводящее тело, обтекаемое токами, можно считать как бы состоящим из множества элементарных электрических вибраторов, а при определении поля, создаваемого этими токами, можно воспользоваться принципом суперпозиции, т.е. рассматривать его как сумму полей элементарных вибраторов.

Перейдем к анализу поля ЭЭВ, расположенного в безграничной однородной изотропной среде, характеризуемой параметрами ε, μ. Ток в вибраторе будем считать известным, т.е. сторонним током, изменяющимся по закону /CT = /mCTcos(ωt+ψ0), где /тст- его амплитуда, а ψ0- начальная фаза (фаза в момент времени t = 0). Так как поле, создаваемое вибратором, в рассматриваемом случае является монохроматическим, удобно воспользоваться методом комплексных амплитуд. Вместо тока /ст

.

Таким образом, задача сводится к нахождению поля по заданному распределению тока. Сначала найдем векторный потенциал А. Введем сферическую систему координат r,θ,φ, ходится в его центре (рис. 5.4).

Комплексная амплитуда векторного потенциала в случае монохроматического поля при произвольном распределении токов в объеме V определяется формулой (2.58). Разобьем интегрирование по объему, занимаемому ЭЭВ, на интегрирование по площади

116

его поперечного сечения ∆S и по длине вибратора l. Для упрощения преобразований будем считать поперечный размер вибратора (диаметр) малым по сравнению с его длиной

l. Учитывая, что представим формулу (2.58) в виде

где - значение координаты точки интегрирования (рис.5.5). При вычислении интеграла (5.1) ограничимся случаем, когда расстояние от вибратора до точек, в которых определяется поле, велико по сравнению с длиной вибратора (r>>l). Тогда в знаменателе подынтегрального выражения величину R можно

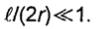Кроме того, по предположению Как известно из курса физики (это будет также показано ниже), отношение c/f равно длине волны λ в среде без потерь с параметрами ε и μ. Поэтому k = 2π/λ, и в (5.1) можно заменить ехр (- ikR) на ехр (- iкг). При такой замене погрешность определения фазы

подынтегрального выражения равна 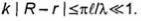С учетом изложенного формула (5.1) принимает вид

Отметим, что сделанное предположение о малости диаметра вибратора d по сравнению с его длиной не является необходимым. Достаточно считать, что d«r.

Вектор Нт связано Аm соотношением Нт =(1/μ) rot Am. Вектор Ёт можно вычислить по формуле (2.57), однако несколько проще, найдя Нm, определить Ет из первого уравнения Максвелла:

В сферической системе координат rotAm вычисляется по

формуле (П. 17). В рассматриваемом случае вектор Аm параллелен оси Z. Чтобы воспользоваться равенством (П. 17), нужно найти

117

Этот результат можно было предвидеть из физических соображений, так как прямолинейный ток вибратора может создать только кольцевые магнитные силовые линии, лежащие в плоскостях, перпендикулярных оси вибратора.

Произведя дифференцирование, получим

Для определения вектора Еm подставим найденный вектор Нmв (5.2). Учитывая, что Нт = Нθт = 0 и дНφт/дφ =0, приходим к выражению

Полученные формулы определяют составляющие комплексных амплитуд векторов Е и Н. Для перехода к мгновенным значениям векторов Е и Н нужно полученные выражения умножить на exp(iωt). а затем отделить действительную часть (Е =

5.3. АНАЛИЗ СТРУКТУРЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ ЭЛЕМЕНТАРНОГО ЭЛЕКТРИЧЕСКОГО ВИБРАТОРА 5.3.1. Деление пространства вокруг вибратора на зоны

Из полученных формул следует, что вектор напряженности электрического поля, создаваемого ЭЭВ, имеет две составляющие Еr и Еθ а вектор Н - одну Нφ Таким образом, в любой точке пространства вектор Е лежит в меридианальной плоскости, т.е. в плоскости, проходящей через ось вибратора и рассматриваемую точку, а вектор Н - в азимутальной плоскости, т.е. в плоскости, перпендикулярной оси вибратора.

Из выражений (5.3), (5.4) и (5.5) видно, что зависимость

амплитуд составляющих векторов Ёт и Нт от расстояния r определеляется величинами 1/(kr), 1 /( kr )2 и 1/( kr)3. При больших значениях kr (kr >>1) величинами 1/( kr)2 и 1 /(kr)3 можно пренебречь по сравнению с 1/( kr), и, наоборот, при малых значениях kr(kr<<1) основными будут величины 1/( kr)3 для составляющих вектора Ё и 1/( kr), 2 - для вектора Н. Поэтому при анализе структуры электромагнитного поля вибратора пространство вокруг вибратора делят на три зоны: дальнюю или волновую ( kr>>1), ближнюю (kr<<1) и промежуточную, где кг соизмеримо с единицей.

118

Величина kr зависит от соотношения между расстоянием от вибратора до точки, в которой вычисляется поле, и длиной волны.

Так как k=2π/λ, то условия kr>>1, kr<<1, kr=1, определяющие дальнюю, ближнюю и

промежуточную зоны, эквивалентны условиям соответственно. Перейдем к анализу свойств электромагнитного поля элементарного электрического вибратора в различных зонах.

5.3.2. Дальняя (волновая) зона

Дальняя или волновая зона, как уже указывалось, характеризуется условием k=2π/λ. Из сравнения формул (5.4) и (5.5) следует, что в этом случае можно пренебречь составляющей Еr по сравнению с Ёθ. Кроме того, в выражениях для Eθ и Нφ можно в квадратных скобках пренебречь слагаемыми 1/( kr)3и I /( kr)2, по сравнению с 1/( kr).

Учитывая, что получаем:

Таким образом, в дальней зоне напряженность электрического поля имеет только составляющую Еθ, а напряженность магнитного поля - составляющую Нφ, которые изменяются синфазно.

Поверхность, во всех точках которой в один и тот же момент времени фаза рассматриваемой функции имеет одинаковые значения, называется поверхностью равных фаз (ПРФ). В случае монохроматического поля на ПРФ постоянна фаза комплексной амплитуды рассматриваемой функции. Соответственно поверхность, на которой постоянна амплитуда (модуль комплексной амплитуды) рассматриваемой функции,

называют поверхностью равных амплитуд (ПРА).

В анализируемом случае ПРФ определяются уравнением r = = const, т.е. представляют собой концентрические сферы с центром в середине вибратора.

Выберем какую-либо поверхность равных фаз и проследим, что происходит с нею с течением времени. Фаза составляющей Ёθ в точке с координатой r0 в момент времени t0 равна ψ0 = ωto- kr0 + π/2. Записывая выражение для фазы в точке с координатой r = r0 + ∆r в момент t1 = t0 + ∆t и приравнивая это выражение ψо, получаем, что ω∆t=k∆r. Следовательно, за время ∆t поверхность равной фазы смещается на расстояние ∆r и в момент t1 представляет собой сферу радиуса rо + ∆r. Скорость перемещения поверхности равной фазы (фазовая скорость)

Как видно, поле (5.6) - электромагнитная волна, расходящаяся от вибратора.

Убедимся, что использованное выше соотношение λ =c/f действительно выполняется. Длиной волны называют кратчайшее расстояние между двумя ПРФ, на которых в один и тот же момент времени значения фазы рассматриваемой функции отличаются на 2π.

Пусть фаза составляющей Еθ на сфере, соответствующей значению r = r0 = const, в момент t= to = const равна ψ=ωto - kr0 + π/2, а на сфере r= r0 + λ равна ψ1 =ωt0-k(r0+λ)+π/2. По определению длины волны должно выполняться соотношение ψ0-ψ1 == 2π. Подставляя значения ψо и ψ1 получаем ωto - kr0 + π/2 - [ωto - k (r0 + λ) + π/2] = kλ= 2π. Следовательно, λ = 2π/k = 2πl(2nf√εμ) = c/f. Длина волны может быть определена также

как расстояние, на которое перемещается ПРФ за период. Так как период Т= 1/f,тоλ= vфT= c/f.

Свободно распространяющиеся волны классифицируют по форме ПРФ. Волны, у которых поверхности равных фаз совпадают с поверхностями равных амплитуд, называют

119

однородными. В нашем случае ПРА определяются уравнением sin θ/r= const и не совпадают с ПРФ. Таким образом, в дальней зоне поле ЭЭВ представляет собой неоднородную сферическую волну, распространяющуюся от вибратора со скоростью света с = 1/√εμ. Векторы Ёт и Нт этой волны взаимно перпендикулярны и перпендикулярны направлению распространения волны. Волны, обладающие таким свойством, называют поперечными.

Распространение волны сопровождается переносом энергии. Средняя за период плотность потока энергии равна Пср = Re П. Комплексный вектор Пойнтинга в рассматриваемом случае является чисто вещественной величиной, поэтому

Из этого выражения следует, что излучение электромагнитной энергии максимально в направлениях, перпендикулярных оси вибратора (θ = π/2) и не зависит от угла φ. Вдоль своей оси (θ = 0 и θ = π) вибратор не излучает. Средняя за период скорость распространения энергии определяется по формуле (1.162). Подставляя в (1.162) выражение (5.7) и учитывая, что

получаем . Используя формулу (1.160), нетрудно

убедиться, что мгновенное значение скорости распространения энергии v3 = v3 cp = roc Таким образом, излучаемая вибратором электромагнитная энергия распространяется вдоль радиусов, проведенных из середины вибратора (т.е. перпендикулярно ПРФ) со скоростью света в данной среде.

Векторы Е и Н изменяются синфазно. На рис. 5.6 показано изменение векторов Е и Н вдоль радиуса r в некоторый момент

времени t = t0, а на рис. 5.7 приведена зависимость значений Е и Н в точке r = r0 от времени.

Важным параметром электромагнитной волны является ее характеристическое сопротивление Zc, равное отношению поперечных к направлению распространения волны составляющих векторов Ёт и Нт. Так как рассматриваемая волна является поперечной, то