Пименов Ю.В., Муравцов А.Д. Техническая электродинамика, 2000

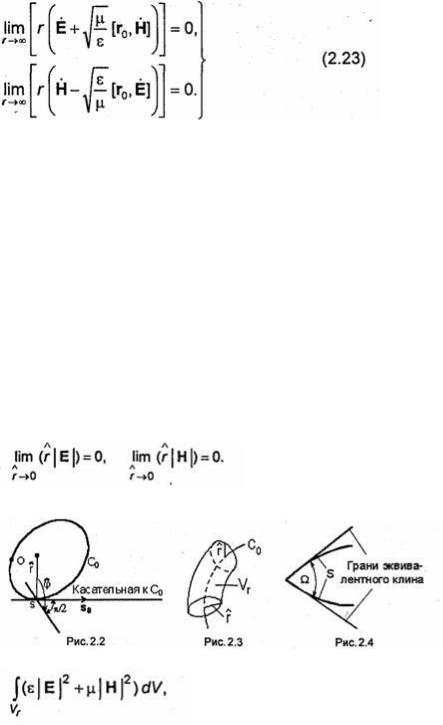
и, следовательно, проведенное выше доказательство справедливо. При r→ ∞ поверхность S' возрастает пропорционально r2. Поэтому для выполнения условия (2.22) необходимо, чтобы абсолютная величина произведения [Ё3,Нз] при r→ ∞ убывала быстрее r-2. Для этого достаточно потребовать, чтобы искомые векторы Е и Н убывали быстрее, чем 1/r.

Таким образом, внешняя задача электродинамики имеет единственное решение, если на поверхности S, ограничивающей объем V, выполняется одно из условий (2.1)-(2.4) и, кроме того, при r→ ∞ векторы Е и Н убывают быстрее, чем 1/r. Последнее всегда имеет место, так как в любых реальных средах имеются потери энергии.

Отметим, что теорему единственности для внешней задачи электродинамики можно доказать и в случае среды без потерь, если вместо условия убывания векторов Е и Н при r→ ∞ быстрее 1/г потребовать выполнения следующих условий:

Предельные соотношения (2.23) называются условиями излучения. Они были сформулированы Зоммерфельдом. Физически эти условия эквивалентны требованию, чтобы при r→ ∞ поле имело характер поперечных волн, распространяющихся вдоль направления r0 (предполагается, что источники поля находятся на конечном расстоянии от поверхности S). Использованный здесь термин "поперечная волна" определен в гл.5.

Отметим, что в тех случаях, когда поверхность S имеет особенности типа изломов, острых кромок и др., для единственности решения краевой задачи электродинамики перечисленных условий недостаточно. Необходимо выполнение дополнительных условий, определяющих поведение составляющих векторов Е и Н вблизи этих особенностей.

К таким условиям относятся, в частности, "условия на ребре", сформулированные Мейкснером для случая идеально проводящих тел. Рассмотрим эти условия. Пусть контур Со представляет собой ребро (острую кромку) идеально проводящей поверхности S.

Введем систему координат 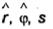(рис. 2.2), связанную с контуром Со, где s - длина дуги,

отсчитываемая вдоль контура Со от некоторой точки О Є Со, а 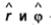- полярные координаты в плоскости, перпендикулярной Со. Условия на ребре записываются в виде

Соотношения (2.24) должны выполняться равномерно по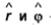

Условия на ребре (2.24) обеспечивают существование интеграла

61

где Vr - объем кольцевой области радиуса r, охватывающей контур Со. Существование этого интеграла эквивалентно выполнению требования ограниченности энергии электромагнитного поля в любом конечном объеме, охватывающем контур Со (рис.2.3). Анализируя соотношения (2.24) совместно с уравнениями Максвелла,

можно показать, что касательные к ребру (контуру Со) составляющие 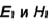должны

быть ограниченными, а нормальные к ребру составляющие 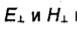могут иметь особенности вида г-x, где 0<х < 1. Для определения параметра и нужно знать внутренний угол так называемого эквивалентного клина, который строится следующим образом. Через произвольную точку М на рассматриваемом ребре Со проводится касательная l к Со и две полуплоскости, касательные к S в точке М, так, чтобы их ребра совпали с l Клин, образованный этими полуплоскостями, и называют эквивалентным клином (на рис. 2.4 показано сечение поверхности S плоскостью, перпендикулярной ребру эквивалентного клина в точке М; касательная l перпендикулярна плоскости рисунка, а ее след совпадает с точкой М). Пусть внутренний угол эквивалентного клина равен Ω. (предполагается, что Ω< π). Анализируя структуры полей вблизи ребра идеально проводящего клина, найденные на основе

решения соответствующих краевых задач, получили, что x = (π - Ω)/(2π - Ω). В частном случае, когда поверхность S имеет острую кромку (например, на краю бесконечно тонкого

экрана), Ω = 0 и х = 1/2. На таком ребре составляющие 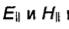имеют особенность вида const, а составляющие обращаются в нуль как

Из приведенного выше доказательства единственности решения краевых задач электродинамики следует, что при отсутствии потерь энергии в области V решение внутренней задачи может быть неединственным. Физически это означает, что в такой системе помимо полей, созданных непрерывно действующими сторонними источниками, могут существовать незатухающие поля, созданные когда-то действовавшими сторонними источниками (но в рассматриваемое время переставшими действовать). Эти поля из-за отсутствия потерь в среде могут существовать сколь угодно долго (например, собственные колебания идеального объемного резонатора).

2.3. ВОЛНОВЫЕ УРАВНЕНИЯ 2.3.1. Общий случай

При решении прямых задач электродинамики требуется найти векторы Е и Н по известным (заданным) сторонним источникам. Предположим, что сторонние источники расположены в безграничной однородной изотропной среде. Для упрощения преобразований будем считать, что σ= 0. Записывая уравнения Максвелла для данного частного случая, получаем

Определение векторов Е и Н непосредственно из системы уравнений (2.25) затруднительно. Поэтому целесообразно преобразовать ее, исключив либо вектор Е, либо вектор Н, т.е. получить из нее такое дифференциальное уравнение, в которое входил бы только один из векторов Е или Н. Для этого возьмем ротор от обеих частей второго уравнения системы (2.25) и изменим порядок дифференцирования по времени и по пространственным координатам. Учитывая известное из векторного анализа равенство

62

где 2≡Δ-оператор Лапласа, и третье равенство рассматриваемой системы, приходим к уравнению

Аналогично выводится и уравнение для вектора Н:

Каждое из векторных уравнений (2.27) и (2.28) эквивалентно трем скалярным уравнениям, получающимся при проецировании векторного уравнения на оси X, Y и Z декартовой системы координат. Эти скалярные уравнения относятся к уравнениям вида

где w и f(x, у, z, f)-искомая и заданная (известная) функции соответственно. Как известно, уравнения вида (2.29) описывают волновые процессы, причем параметр v равен скорости этого процесса. Такие уравнения принято называть неоднородными уравнениями Даламбера или неоднородными волновыми уравнениями. Уравнения (2.27) и (2.28)

отличаются от (2.29) только тем, что входящие в них функции являются векторными.

Уравнения такого типа называют неоднородными векторными уравнениями Даламбера или неоднородными векторными волновыми уравнениями. Аналогичные уравнения,

правые части которых равны нулю, называют однородными векторными уравнениями Даламбера (однородными векторными волновыми уравнениями).

В дальнейшем будет показано, что входящий в уравнения

(2.27) и (2.28) параметр 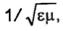являющийся аналогом параметра v в (2.29), в случае среды без потерь также представляет собой скорость распространения электромагнитного поля и равен скорости света ев рассматриваемой среде. Этот результат не является неожиданным, так как свет - это электромагнитные волны определенного диапазона частот.

Без затруднений записываются аналогичные уравнения для векторов Е и Н и в том случае,

когда σ≠ 0 (см., напр., [1]).

2.3.2. Монохроматическое поле

В случае монохроматического поля полная система уравнений Максвелла в комплексной форме, учитывающая сторонние электрические источники, имеет вид

Предположим, что среда, заполняющая рассматриваемую часть пространства, является однородной и изотропной. Возьмем ротор от обеих частей второго уравнения системы (2.30) и исключим вектор Н, используя первое уравнение. Учитывая формулу (2.26) и

равенство справедливое для однородной изотропной среды, придем к уравнению

Очевидно, что такие же уравнения связывают между собой комплексные амплитуды

63

Если в рассматриваемой области отсутствуют сторонние источники, уравнения

(2.31) и (2.32) упрощаются:

Для перехода к случаю среды без потерь в уравнениях (2.30)-(2.34) нужно положить . Каждое из векторных уравнений (2.33) и (2.34) эквивалентно трем однотипным скалярным

уравнениям для декартовых составляющих соответствующего вектора: ∆2w+k2w = 0, где

w-любая из составляющих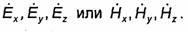

2.4. ЭЛЕКТРОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ 2.4.1. Общий случай

Выведенные в предыдущем разделе дифференциальные уравнения позволяют в принципе определить векторы Е и Н через функции jст и ρст. Однако наличие в их правых частях выражений grad ρст и rot jст в ряде случаев несколько затрудняет получение

удобных расчетных формул. Поэтому указанные уравнения обычно используют в тех случаях, когда сторонние источники расположены за пределами рассматриваемой области, т.е. когда уравнения (2.27) и (2.28) становятся однородными и соответственно уравнения (2.31) и (2.32) переходят в (2.33) и (2.34).

В общем случае для определения векторов поля по заданным источникам обычно применяют искусственный прием: сначала находят вспомогательные функции, а потом через них вычисляют векторы Е и Н. Эти вспомогательные функции можно ввести различным образом в зависимости от специфических особенностей анализируемой задачи. Для упрощения решения многих задач вводят так называемые электродинамические потенциалы. Рассмотрим систему уравнений Максвелла (2.25). Последнее уравнение этой системы представляет собой четвертое уравнение Максвелла div В = 0, записанное для случая однородной изотропной среды. Так как дивергенция ротора любого вектора равна нулю (div rot a = 0), то из уравнения div В = 0 следует, что вектор В можно представить в виде В = rot А. При этом вектор

При известном векторе А уравнение (2.35) позволяет однозначно найти вектор Н. Однако оно допускает некоторый произвол в определении вектора А. Действительно, если вместо А взять вектор A1= А + grad ψ, где ψ - произвольная скалярная функция, то значение вектора Н не изменится, так как

Неоднозначность определения вектора А будет использована при выводе дифференциального уравнения для А.

Подставим выражение (2.35) во второе уравнение системы (2.25) и изменим порядок дифференцирования по времени и пространственным координатам. Объединив затем векторы Е и дА/дt под знаком ротора, получим rot(E + дА/дt) = 0. Учитывая тождество (2.36), можно положить, что стоящее под знаком ротора выражение равно - grad и, где и- некоторая скалярная функция, или

Знак минус перед grad и в формуле (2.37) введен, чтобы в случае электростатического поля функция и совпадала с обычным электростатическим потенциалом.

64

Таким образом, все векторы, определяющие электромагнитное поле, выражаются через две функции: векторный потенциал А и скалярный потенциал и. Следовательно, задача состоит теперь в том, чтобы найти функции А и и. Подставляя (2.35) и (2.37) в первое уравнение системы (2.25) и преобразовывая левую часть получающегося при этом соотношения с помощью тождества (2.26), приходим к равенству

Упростим уравнение (2.38). Как уже отмечалось, вектор А определен с точностью до градиента произвольной скалярной функции. Следовательно, можно потребовать, чтобы вектор А удовлетворял добавочному условию. Потребуем, чтобы

Соотношение (2.39) принято называть условием калибровки. учетом (2.39) уравнение (2.38) принимает вид

Аналогичное уравнение получается и для скалярного потенциала и. Подставляя (2.37) в третье уравнение системы (2.25), получаем

Используя условие калибровки (2.39) и тождество div grad и = 2u, приходим к уравнению

(2.41)

Таким образом, векторный и скалярный потенциалы, как и векторы Е и Н, удовлетворяют неоднородным уравнениям Даламбера. Однако правые части уравнений для потенциалов имеют более простой вид. Поэтому уравнения (2.40) и (2.41) оказываются более удобными при решении многих конкретных задач.

Найдем частные решения уравнений (2.40) и (2.41), считая функции jст и ρст. известными. Вначале рассмотрим уравнение (2.41). Предположим, что электрическое поле создается точечным неподвижным зарядом постоянной величины Q = const, расположенным в начале координат, вектор Е в этом случае определяется выражением (1.7). Так как поле не должно зависеть от времени, то dA/дt = 0 и соотношение (2.37) принимает вид Е =- grad и. Расписывая grad и в сферической системе координат r,θ,φ (см. приложение 4) и учитывая, что вектор Е в рассматриваемом случае может зависеть только от координаты r (от расстояния от заряда Q до точки наблюдения), получаем

где r0 - координатный орт переменной r. Подставляя выражение (2.42) в (1.7) и выполняя интегрирование по переменной r, находим функцию и:

Постоянная интегрирования в (2.43) принята равной нулю, чтобы при r→ ∞ функция и обращалась в нуль. Формула (2.43) полностью совпадает с известным из курса общей физики выражением для электростатического потенциала точечного заряда (см. замечание по поводу выбора знака перед grad и в выражении (2.37)). Если заряд сосредоточен в малом элементе объема dV с плотностью ρст, то и =ρстdV/(4πεR), где R- расстояние от элемента dV до точки наблюдения. От этой формулы легко перейти к выражению для

65

электростатического потенциала, создаваемого произвольным распределением зарядов в объеме V. В соответствии с принципом суперпозиции получаем

Значение и, определяемое формулой (2.44), можно рассматривать как решение уравнения

получающегося из равенства (2.41), если в последнем положить д2u/дt2=0. Уравнение

(2.45) называют уравнением Пуассона.

Предположим теперь, что поле также создается точечным зарядом, расположенным в начале координат, но величина этого заряда изменяется со временем Q = Q (t). Тогда в любой точке, кроме начала координат, потенциал и будет удовлетворять однородному уравнению Даламбера

Для решения уравнения (2.46) удобно использовать сферическую систему координат r, θ, φ (рис.2.5). Оператор Лапласа 2 в этой системе координат определяется формулой (П. 18). Так как лоле создается точечным зарядом, расположенным в начале координат, то потенциал и не должен зависеть от углов θ и φ. Поэтому уравнение (2.45) можно переписать в виде

- произвольные дважды дифференцируемые функции аргументов t-rlc и t+rlc соответственно. В том, что функции f1(t-r/c) и f2(t+r/c) удовлетворяют (2.47), можно убедиться непосредственной подстановкой их в это уравнение. Таким образом, скалярный потенциал и можно представить в виде

66

Первое слагаемое в выражении (2.48) представляет собой волну, распространяющуюся из начала координат вдоль радиусов r со скоростью света Действительно,

функция в фиксированный момент времени t имеет одинаковые значения на

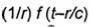принято называть расходящимися сферическими волнами. Соответственно второе слагаемое в выражении (2.48) представляет собой сферическую волну, распространяющуюся из бесконечности со скоростью света с и сходящуюся к началу координат. Отметим существенную особенность функций, описывающих волновые процессы. Они всегда содержат множители вида f(t±r/v), характер зависимости которых от расстояния вдоль направления распространения волны в фиксированный момент времени повторяет характер их зависимости от времени в фиксированной точке пространства, а v- скорость распространения волны.

Если источники поля сосредоточены в ограниченной области, то сходящаяся сферическая волна может возникнуть только в результате отражения расходящейся сферической волны. Так как пространство считается однородным, то отраженной волны не может быть, и функцию f2(t +r/с) нужно считать равной нулю. Следовательно, и = f1(t- r/c)/r. Значения потенциала и должны быть связаны с интенсивностью источников поля. В рассматриваемом случае источником поля является точечный заряд Q(t). Полученное выражение для и должно быть справедливым при любом законе изменения функции Q(t). Так как в статическом случае потенциал и определяется формулой (2.43), естественно предположить, что f1-r/c) = Q(t-r/c)/(4πε). Тогда u=Q(t-R/c)/(4πεr). Если заряд сосредоточен в малом элементе объема dV с плотностью ρст = ρст(t), то скалярный потенциал и = pСТ(t- R/c)dV/(4πεR), где R-как и ранее, расстояние от элемента dV до точки наблюдения. От этой формулы легко перейти к выражению для скалярного потенциала, обусловленного произвольным распределением сторонних зарядов в объеме V:

декартовы координаты элемента dV; x, у, z -декартовы координаты точки наблюдения N;

элемент объема 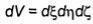(рис.2.6).

Выражение (2.49) является частным решением неоднородного уравнения Даламбера (2.41). Отметим, что приведенный здесь вывод не является строгим, он имеет лишь наводящий характер. Строгий вывод формулы (2.49) можно найти, например, в [12].

67

Аналогично можно записать и решение уравнения (2.40). Для этого нужно в (2.49) заменить и на А, ρст на jСТ и ε на 1/μ. В результате получим

Из (2.49) и (2.50) следует, что для вычисления электродинамических потенциалов и и А в произвольной точке пространства N=N(х, у, z) в момент времени t нужно брать значения токов и зарядов в каждом элементе dV в более ранний по сравнению с t момент времени t’= t-R/c, определяемый расстоянием R от элемента dV до точки наблюдения N(х, у, z) (рис.2.6). Иными словами, влияние источников электромагнитного поля проявляется не мгновенно: требуется некоторое время t = Rlc, за которое электромагнитные колебания, вызванные зарядами и токами в элементе dV, успеют распространиться от элемента dV до точки наблюдения. Поэтому функции А и и в форме (2.50) и (2.49) часто называют запаздывающими потенциалами.

2.4.2. Монохроматическое поле

Рассмотрим систему уравнений Максвелла для монохроматического поля, записанную для комплексных амплитуд векторов Е и Н:

Используя равенство div(μHm) = O, являющееся следствием второго уравнения системы (2.51), представим вектор Нm в виде

где Аm-комплексная амплитуда некоторого, пока неизвестного,

вектора А. Подставляя (2.52) во второе уравнение системы (2.51) и учитывая тождество (2.36), получаем

где Ăт - комплексная амплитуда некоторой, пока неизвестной, скалярной функции и. Подставляя (2.52) и (2.53) в первое уравнение системы (2.51) и учитывая (2.26), имеем

Соотношение (2.52) допускает некоторую свободу в определении вектора Аm (см. замечание к формуле (2.37)). Поэтому с целью упрощения уравнения (2.54) потребуем выполнения дополнительного условия

которое обычно называют условием калибровки Лоренца. При этом равенство (2.54) переходит в неоднородное векторное уравнение Гельмгольца

Отметим, что условие калибровки (2.55) позволяет выразить через один векторный потенциал не только вектор Нm, но и вектор

Ёm. Действительно, выражая йт из (2.55) и подставляя в (2.53), получаем

68

Предположим вначале, что среда, в которой ищется поле, является идеальным

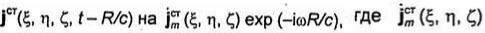-комплексная амплитуда плотности сторонних электрических токов. Так как ,

Для перехода к случаю среды с потерями достаточно в (2.58) заменить μ на μ и k на

Подставляя (2.53) в равенство являющееся следствием первого уравнения системы (2.51), и учитывая условие калибровки (2.55) и тождество (П.ЗО), приходим к уравнению Гельмгольца для скалярного потенциала:

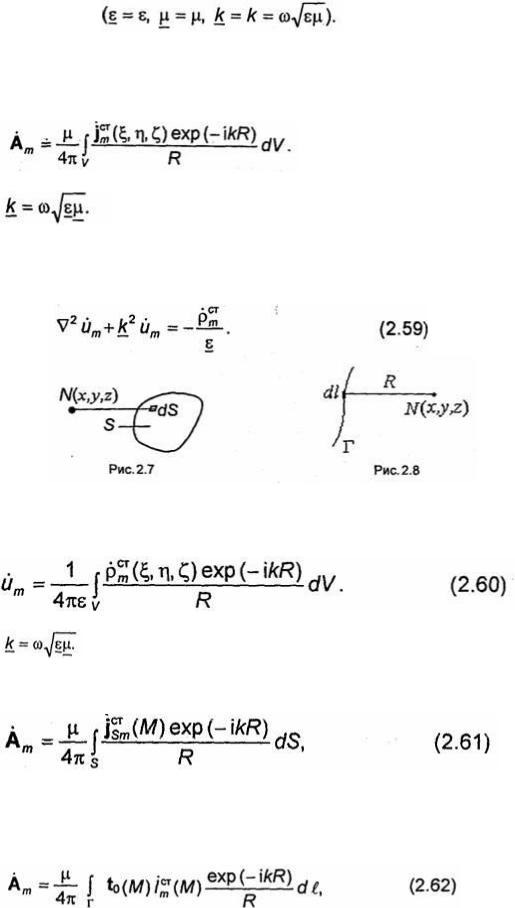
В случае однородной среды без потерь (ε =ε,μ = μ, k = к) решение уравнения (2.59) может

быть получено из (2.58) заменой функции 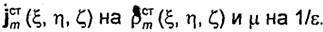. При этом имеем

Для перехода к случаю среды с потерями нужно в (2.60) заменить ε на ε и k на

Полученные формулы соответствуют распределению сторонних источников в некотором объеме V. Если сторонние электрические токи являются поверхностными и распределены по некоторой поверхности S, то

где M-точка на поверхности S, принадлежащая элементу dS, a R-расстояние от точки М до точки наблюдения N=N(х, у, z) (рис. 2.7).

В случае линейного стороннего тока jст, распределенного

вдоль контура Г, комплексная амплитуда векторного потенциала определяется выражением

69

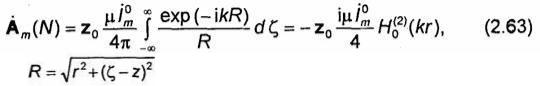
где to(M) - орт касательной к контуру Г в точке М, направление которой совпадает с направлением тока; dl - элемент контура Г, содержащий точку М; R-расстояние от точки МЄ Г до точки наблюдения N (рис. 2.8).

Аналогично видоизменяется формула (2.60) для скалярного потенциала и в случае поверхностных и линейных зарядов.

2.4.3. Плоские задачи электродинамики

При построении электродинамических моделей реальных задач часто считают, что поле, созданное сторонними источниками, и поперечное сечение рассматриваемой области не зависят от одной из декартовых координат, например от z. Такие модели называют плоскими (двумерными) задачами. Простейшим сторонним источником в этом частном случае является синфазная токовая нитьлинейный электрический ток, текущий параллельно оси Z, амплитуда и фаза которого не зависят от z. Вычислим соответствующий ему векторный потенциал.

Предположим, что линейный электрический ток течет вдоль

оси Z. То/да, полагая в (2.62) 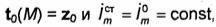получаем

оси Z, до точки наблюдения N(х, у, z); - расстояние от точки N(х, у, z) до оси Z, a H (2)0 (kR)-функция Ханкеля второго рода нулевого порядка от аргумента кг, связанная с функциями Бесселя Jo(kr) и Неймана N0(kr) нулевого порядка соотношением

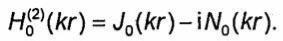При r→0 функция

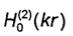имеет логарифмическую особенность, а при r→0 справедливо асимптотическое

соотношение 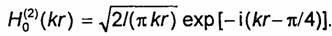Как видно, на больших расстояниях от источника (kr>>1) поверхности, на которых фаза функции Аm одинакова во всех точках, описываются уравнением r = const и представляют собой поверхности соосных круговых цилиндров, бесконечно протяженных вдоль оси z. С учетом знака в показателе степени множителя ехр [— i (kr—π/4)] поле, создаваемое синфазной токовой нитью, может быть названо цилиндрической волной, распространяющейся от источника к бесконечности.

Так как в рассматриваемом случае поле не зависит от z, a

вектор Am=zQAm, то divAm=0 и выполняется простое соотношение Ёm = -iωAm.

Отметим, что хотя до сих пор при записи формул (2.50), (2.58) и (2.61)-(2.63) ДЛЯ векторного потенциала речь шла о поле, создаваемом сторонними источниками, аналогичные формулы имеют место и для векторного потенциала, создаваемого другими токами, например токами, возникающими на металлическом объекте под воздействием поля сторонних источников.

70