Пименов Ю.В., Муравцов А.Д. Техническая электродинамика, 2000

Действительно, электромагнитное поле отдает энергию току проводимости, если оно ускоряет движение заряженных частиц, образующих ток. Для этого вектор напряженности электрического поля Е должен иметь составляющую, ориентированную вдоль линий тока, т.е. чтобы скалярное произведение векторов Е и jст было больше нуля.

Рассмотрим более подробно формулы, определяющие энергию электромагнитного поля. Подынтегральные выражения в

можно интерпретировать как мгновенные значения объемных плотностей энергии электрического и магнитного полей соответственно, а их сумму

- как объемную плотность полной энергии электромагнитного поля.

Подчеркнем, что принцип суперпозиции, которому удовлетворяют векторы напряженностей электрического и магнитного полей, не распространяется на энергию. Действительно, пусть энергии полей E1, H1 и Е2, Н2, существующих по отдельности в области V, равны соответственно W1 и W2. Тогда энергия суммарного поля Е = Е1 + Е2, Н

=Н1 + Н2 определится выражением

-взаимная энергия полей. Взаимная энергия W12 может быть как положительной, так и отрицательной. Если векторы Е1 и Е2, а также H1 и Н2 взаимно перпендикулярны, то

W12 = 0.

В случае переменных процессов распределение электромагнитной энергии непрерывно изменяется. Это изменение в каждой данной точке можно определить на основе уравнения (1.122), которое удобно представить в виде

где pст =-E jст и pn = Ej-мгновенные значения плотностей мощности сторонних источников и мощности джоулевых потерь соответственно. При переходе от соотношения (1.122) к уравнению (1.136) учтены формулы (1.125) и (1.135). Уравнение (1.136) является

дифференциальной формой теоремы Пойнтинга.

1.8.3. Активная, реактивная и комплексная мощности

Рассмотрим выражение для мгновенных значений мощности Р в электрической цепи, в

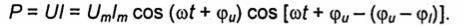. После элементарных тригонометрических преобразований представим Р в виде суммы двух слагаемых:

51

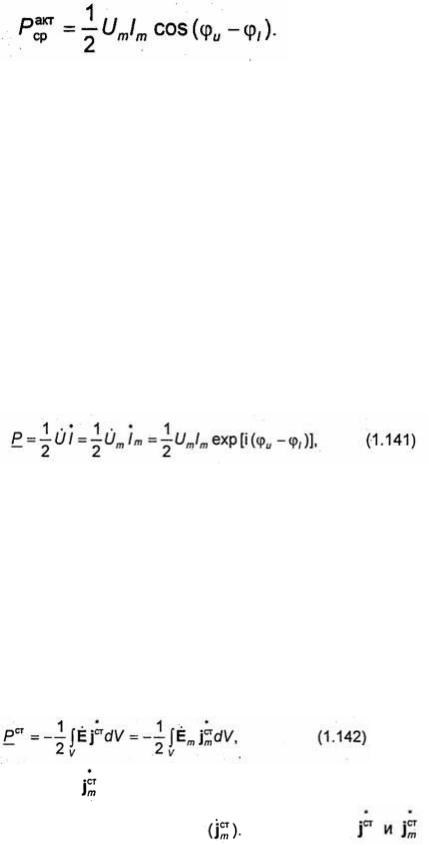
Составляющую РАКТ называют активной мощностью. Так как в любой цепи

то активная мощность не может быть отрицательной . Среднее за период значение активной мощности

Составляющую Рреак называют реактивной мощностью.

Как видно из (1.139), она изменяется с частотой 2ώ и в течение периода Т= 1/f дважды изменяет знак. Среднее за период значение реактивной мощности равно нулю. Поэтому среднее за период значение мощности Р совпадает со средним за период значением

активной мощности: При анализе гармонических колебаний в электрических цепях широко используют метод

комплексных амплитуд. При этом вместо мгновенных значений напряжения U и тока / вводят в рассмотрение комплексные функции Ủ и Ỉ соответствующие им комплексные амплитуды Ủ и Ỉm , связанные обычными (см.1.6)

соотношениями: 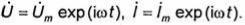Для перехода от мгновенных значений напряжения и тока к их комплексным функциям Ủ и Ỉ достаточно заменить

. Однако метод комплексных амплитуд непосредственно применим только в случае линейных соотношений. Поэтому переходить в выражениях для мгновенных значений мощности к комплексным функциям обычными заменами U на Ủ и / на Ỉ не имеет смысла. В то же время можно ввести понятие комплексной мощности, удобное для практического использования. Назовем комплексной мощностью функцию

где символ * означает, что взята комплексно-сопряженная величина: функции Ỉ и Ỉm являются комплексно сопряженными Ỉ и Ỉm соответственно. Как видно из (1.141), комплексная мощность не зависит от времени. Отделяя в (1.141) действительную и мнимую части, замечаем, что действительная часть комплексной мощности совпадает со средним за период значением мощности

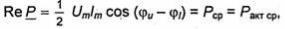а мнимая часть равна амплитуде реактивной

мощности Аналогично может быть введена комплексная мощность и в любом другом случае. Рассмотрим, например, мощности, входящие в уравнение (1.126).

Заменяя в (1.128) вектор Е комплексным вектором Ё, ajст- вектором jст, комплексно сопряженным с jст, и умножая результат

на 1/2, приходим к выражению для комплексной мощности сторонних источников:

где - вектор, комплексно сопряженный с комплексной амплитудой плотности

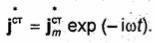Действительная часть комплексной мощности сторонних источников (RePст) равна средней за

период мощности сторонних источников, которая в свою очередь равна средней за период активной мощности сторонних источников:

Мнимая часть комплексной мощности сторонних источников

равна амплитуде реактивной мощности сторонних источников.

Преобразовывая аналогичным образом формулу (1.127) для мгновенных значений мощности джоулевых потерь Рп, получаем вещественную величину, равную среднему за период значению мощности джоулевых потерь в объеме V:

Рассмотрим выражение для потока энергии через поверхность

S. Переходя в (1.134) к комплексным векторам Е и Н, получаем выражение для комплексного потока энергии через поверхность S:

- комплексный вектор Пойнтинга.

Действительная и мнимая части РЕ равны соответственно среднему за период потоку энергии через поверхность S и амплитуде реактивного потока энергии через S. Аналогично действительная и мнимая части комплексного вектора Пойнтинга представляют собой среднюю за период плотность потока энергии в рассматриваемой точке пространства и амплитуду плотности реактивного потока энергии в той же точке соответственно.

1.8.4. Уравнение баланса комплексной мощности

Уравнение баланса комплексной мощности может быть получено либо из уравнений Максвелла в комплексной форме, либо непосредственно из теоремы Пойнтинга. Второй путь короче. При этом вывод упрощается, если в качестве исходного использовать уравнение баланса мгновенных значений мощности в форме (1.123). Перейдем от мгновенных значений мощностей, входящих в (1.123), к комплексным мощностям на основе приема, описанного в 1.8.3. Все подынтегральные выражения в (1.123) содержат произведения двух векторов. Заменим в этих произведениях первый вектор соответствующим ему комплексным вектором (например, вектор Е - на Ё), а второй вектор - соответствующим ему комплексно-сопряженным

вектором (например, jст-нa jст). Умножая обе части получающегося при этом равенства на 1/2, приходим к соотношению

Вычисляя производные по t и учитывая обозначение (1.145), получаем уравнение баланса комплексной мощности:

53

Проанализируем это уравнение. Используя формулы (1.142)—(1.144), перепишем его в виде

-соответственно средние за период значения энергий электрического и магнитного полей в объеме V. Из равенства комплексных величин следуют отдельные равенства для их действительных и мнимых частей. Отделяя в (1.147) действительные части, получаем

Левая часть равенства (1.148) представляет собой среднюю за период мощность сторонних источников, которая равна также средней за период активной мощности сторонних источников. Второе слагаемое в правой части (1.148) равно среднему за период потоку энергии через поверхность S и соответственно среднему за период активному потоку энергии через ту же поверхность:

Поэтому равенство (1.148) эквивалентно соотношению

Таким образом, уравнение (1.148) представляет собой уравнение баланса средних за период мощностей. Уравнение (1.148) иногда называют также уравнением баланса активных мощностей.

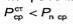средний поток энергии отрицателен, т.е. направлен из окружающего пространства в объем V.

Отделяя в (1.147) мнимые части, получаем

Входящие в (1.150) величины 1тРст и ImPΣ; равны соответственно амплитуде реактивной мощности сторонних источников и амплитуде реактивного потока энергии через поверхность S. Поэтому уравнение (1.150) иногда называют уравнением баланса реактивных мощностей.

Реактивный поток энергии изменяется со временем по гармоническому закону с удвоенной круговой частотой 2ω. В течение периода он половину времени имеет положительное значение, т.е. энергия поступает в окружающее пространство, а другую половину - отрицательное, т.е. энергия поступает из окружающего пространства, в объем V. Среднее за период значение реактивного потока энергии равно нулю. Таким образом, из (1.150) следует, что разность между амплитудами реактивной мощности сторонних источников и реактивного потока энергии через ограничивающую этот объем поверхность S равна умноженной на 2ω разности между средними за период значениями энергий магнитного и электрического полей в объеме V.

Предположим, что объем V представляет собой изолированную систему (например, ограничен идеально проводящей поверхностью). Тогда поток комплексного вектора Пойнтинга через S будет равен нулю, и уравнения (1.149) и (1.150) примут вид

54

В этом случае в объеме V энергия электрического поля будет периодически преобразовываться в энергию магнитного поля и обратно. Если средние за период значения энергий электрического и магнитного полей равны, т.е.

то этот процесс протекает без участия источников, и мощность сторонних источников

оказывается чисто активной (ImРст = 0). Если же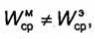, то периодическое преобразование энергии электрического поля в энергию магнитного поля и обратно возможно только при участии сторонних источников. При этом реактивная мощность

сторонних источников будет отлична от нуля 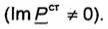. Если в изолированной области мощность сторонних источников является чисто активной, то имеет место резонанс. Из изложенного следует, что для резонанса необходимо выполнение условия (1.153). Отношение

где , называют добротностью изолированной системы. Выражение (1.154) можно переписать в иной форме. Заменяя со на 2π/Т, получаем

где W - изменение энергии электромагнитного поля системы за период. Таким образом, добротность изолированной системы - это увеличенное в 2π раз отношение запаса энергии

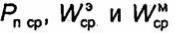определяются выражениями

1.8.5. Скорость распространения электромагнитной энергии

Как уже отмечалось, из теоремы Пойнтинга (1.126) следует возможность распространения в пространстве энергии электромагнитного поля. Вычислим скорость, с которой происходит это распространение. Выделим в рассматриваемой части пространства так называемую энергетическую трубку, т.е. трубку на боковой поверхности которой перпендикулярная к ней составляющая вектора Пойнтинга (Пп) тождественно равна нулю (рис.1.24). При этом условии средний за период поток энергии через поперечное сечение трубки при отсутствии джоулевых потерь не изменяется вдоль трубки.

55

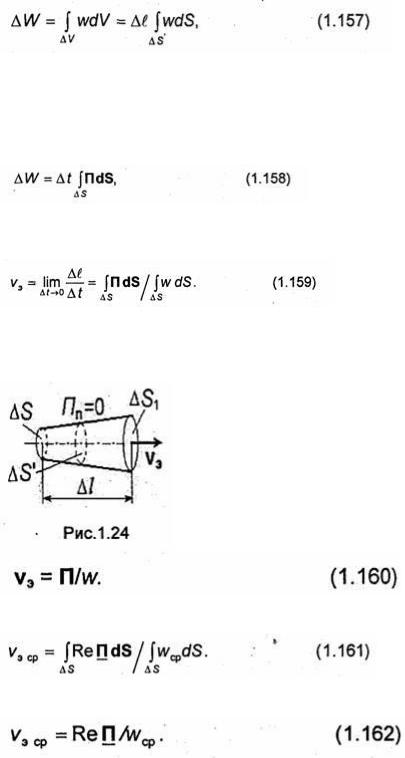
Энергия электромагнитного поля ΔW, прошедшая за время Δt через поперечное сечение трубки S, будет распределена с плотностью w в объеме ΔV, ограниченном боковой поверхностью трубки и поперечными сечениями S и S1 находящимися на расстоянии Δl друг от друга (рис.1.24). Эта энергия может быть вычислена по формуле

где S' - некоторое поперечное сечение трубки, расположенное между сечениями S и

ΔS1.

Будем называть скоростью распространения энергии v3 предел отношения l кΔt при

Δt→O.

При достаточно малых значениях Δt можно считать, что в пределах Δt вектор Пойнтинга не изменяется. Поэтому наряду с (1.157) должно выполняться соотношение

где dS=l0dS, а l0 - единичный вектор, перпендикулярный к S и направленный в сторону ΔS1. Приравнивая правые части выражений (1.157) и (1.158) и переходя к пределу при Δt→0, находим

При выводе формулы (1.159) учтено, что в пределе при Δt→0сечение S' совпадает с ΔS. Если Е и Н, а следовательно, П и w не изменяются вдоль сечения ΔS, формула (1.159) упрощается. Так как в этом случае направление вектора Пойнтинга совпадает с направлением распространения энергии, то

Нетрудно показать, что в случае монохроматического поля среднее за период значение скорости распространения энергии v3cp определяется формулой

Если значения вектора П и функции wcp одинаковы во всех точках сечения AS, выражение (1.161) может быть записано в виде

Таким образом, в данной главе рассмотрены основные уравнения электродинамики. Перейдем к рассмотрению вопроса о применении этих уравнений к решению конкретных задач.

56

Глава 2 ПОСТАНОВКА ЗАДАЧ ЭЛЕКТРОДИНАМИКИ

2.1. КЛАССИФИКАЦИЯ ЗАДАЧ ЭЛЕКТРОДИНАМИКИ

При решении многих проблем радиотехники, электро- и радиосвязи, радиофизики и других научно-технических отраслей необходимо знать структуру электромагнитного поля в рассматриваемой части пространства. К таким проблемам относятся, например, разработка излучающих систем (антенн) и повышение их помехозащищенности, обеспечение электромагнитной совместимости радиотехнических устройств и систем, разработка различных линий передачи энергии и многие другие. Для расчета электромагнитного поля в каждом конкретном случае требуется решить соответствующую электродинамическую задачу.

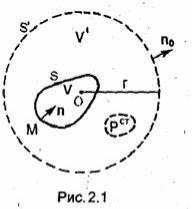
Выделяют два класса задач электродинамики, которые называют прямыми и обратными задачами. Прямые задачи электродинамики (их часто называют также задачами анализа) состоят в определении электромагнитного поля, которое создается в рассматриваемой части пространства под воздействием известных (заданных) источников. Обратные задачи электродинамики (обычно их называют задачами синтеза) состоят в определении системы источников, которые создают электромагнитное поле, обладающее требуемой (заданной) структурой. Прямые задачи электродинамики часто формулируют как краевые задачи, состоящие в нахождении электромагнитного поля, удовлетворяющего определенным (краевым) условиям на границе рассматриваемой части пространства. Различают внутренние и внешние краевые задачи .Пусть задана некоторая область V, ограниченная замкнутой поверхностью S (см. рис. 1.23). Определение поля внутри области V называют внутренней задачей. Соответственно определение поля во всем пространстве, внешнем по отношению к области V (рис. 2.1), называют внешней задачей.

Возникающие на практике электродинамические задачи обычно весьма сложны,

и их решение удается получить лишь после введения ряда упрощающих предположений. Поэтому практически всегда вместо реальной задачи рассматривают некоторую модельную задачу, которая в той или иной степени отражает реальную ситуацию. Часто исходную задачу удается разбить на ряд более простых, каждая из которых позволяет учесть один или несколько влияющих факторов.

2.2. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ЭЛЕКТРОДИНАМИКИ 2.2.1. Вводные Замечания

Уравнения Максвелла являются дифференциальными уравнениями в частных производных. Такие уравнения допускают множество решений. Однако из общих физических представлений очевидно, что при полном повторении условий эксперимента распределение поля должно быть одинаковым. Следовательно, в каждом конкретном случае электромагнитное поле должно удовлетворять не только уравнениям Максвелла, но и некоторым дополнительным условиям. Эти дополнительные условия определяются специальными теоремами, называемыми теоремами единственности решения задач

57

электродинамики. Ограничимся доказательством этих теорем для краевых задач в случае монохроматического поля, причем будем считать, что в рассматриваемой части пространства происходит (хотя бы и очень слабое) поглощение энергии, т.е. что Рпср ≠ О.

2.2.2. Единственность решения внутренних задач электродинамики

Покажем, что внутренняя задача электродинамики имеет единственное решение, если на граничной поверхности S (см. рис.1.23) выполняется одно из следующих четырех условий:

вкаждой точке М поверхности S задана проекция вектора Е на плоскость Р[М), касательную к S в точке М (Е-задача):

вкаждой точке М поверхности S задана проекция вектора Н на плоскость Р(М) (Н-задача):

на одной части поверхности S (обозначим ее S1) задана проекция Еτ вектора Ё, а на другой части (S2) - проекция Нτ вектора Н на плоскость Р{М), причем S1 + S2 = S (ЕН-задача):

в каждой точке М поверхности S проекции векторов Ё и Н на оскость Р(М) связаны соотношением

Условие (2.4) часто называют импедансным краевым условием. Очевидно, что векторы Et и Ht., образующиеся при проецировании Ёτ и Нτ на плоскость Р(М), имеют различное

и рассмотрим их разность:

и одинаковым краевым условиям на поверхности S. Уравнения Максвелла для поля Ё3,Н3 получаются почленным вычитанием уравнения (2.8) из (2.7). При этом векторы jCT сокращаются, и уравнения Максвелла для поля Ё3, Н3 принимают вид

На поверхности S поле Ё3, Н3 должно удовлетворять следующим краевым условиям: в случае Е-задачи

58

вслучае Н-задачи

вслучае Е-задачи

вслучае импедансного краевого условия (2.4)

Составим уравнение баланса для средней за период мощности разностного поля Ё3, Н3. Так как векторы Ё3, Н3 удовлетворяют уравнениям Максвелла (2.9), то мощность

сторонних источников разностного поля 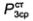равна нулю, и уравнение (1.148) принимает вид

Так как dS = nodS, где п0-орт внешней нормали к поверхности S, то произведение [Ё3, H3]dS определяется только касательными составляющими векторов Ё3 и Нз. В случае

проводимости . В этом случае уравнение (2.15) принимает вид

Так как то из равенства (2.16) следует, что Ё3 = 0. Используя второе уравнение Максвелла, записанное относительно векторов Ё3 и Н3, получаем Н3 = 0. Следовательно, Ё2 = Ё1 и Н2 = Н1, т.е. задача имеет единственное решение.

Рассмотрим теперь краевое условие (2.4). В этом случае подынтегральное выражение во втором слагаемом в уравнении (2.14) может быть преобразовано следующим образом:

При этом из (2.14)

получаем соотношение

Так как и, кроме того, выполняется условие (2.5), то равенство (2.17) возможно только при Ё3 = 0. Таким образом, и в этом случае задача имеет единственное решение.

Единственность решения в более общем случае, когда

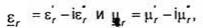доказывается аналогично на основе анализа уравнения (2.14). При этом выражение для средней за период мощности потерь в объеме V для поля Ё3,Н3 должно быть записано на основе равенства (1.156).

59

2.2.3. Единственность решения внешних задач электродинамики

В случае внешней задачи электродинамики поверхность S не охватывает рассматриваемую часть пространства, простирающуюся до бесконечности. Поэтому для единственности решения кроме одного из условий (2.1)-(2.4) требуется задать дополнительное условие, характеризующее поведение векторов Е и Н в точках, бесконечно удаленных от поверхности S. Выясним, каким должно быть это дополнительное условие.

Пусть на S выполняется одно из условий (2.1)-(2.4). Предположим, что имеется два решения задачи E1, H1 и Е2, Н2, и введем в рассмотрение разностное поле Е3, Н3 по формулам (2.6). Как и в случае внутренней задачи электродинамики, векторы Ё3 и Н3 удовлетворяют уравнениям Максвелла (2.9) и одному из условий (2.10)—(2.13) на

поверхности S. Из произвольной точки 0 внутри области V мысленно проведем сферу радиуса г так, чтобы вся область V и все сторонние источники оказались внутри этой сферы. Объем, заключенный между поверхностями S и S', обозначим через V (рис.2.1). Составим уравнение баланса для средних за период значений мощности поля Ё3,Н3 в объеме V:

Перейдем в уравнении (2.18) к пределу при r→ ∞. Тогда область V распространится на все пространство, внешнее по отношению к области V. Если в пределе третье слагаемое в левой части уравнения (2.18) окажется равным нулю, то получающееся при этом соотношение

не будет иметь принципиальных отличий от аналогичного уравнения (2.14) для внутренней задачи электродинамики, и, следовательно, рассматриваемая задача также будет иметь единственное решение. Действительно, при выполнении условий (2.1)-(2.3), второе слагаемое в левой части (2.19) обращается в нуль, и это уравнение принимает вид

В частном случае, когда потери в среде обусловлены только наличием проводимости, т.е.

когда 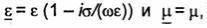уравнение (2.20) записывается в форме

Так как а то из (2.21) получаем Ё3 =0, а из второго уравнения Максвелла - Н3 = 0. Следовательно, Ё2 = Ё1 и Н2 = Н1.

Если на поверхности S выполняется условие (2.4), то из уравнений (2.19) и (2.13) имеем

откуда также следует единственность решения.

В более общем случае, когда 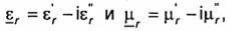единственность решения доказывается также на основе формулы (2.20) для краевых условий (2.1)-(2.3) и на основе уравнения (2.19) в случае краевого условия (2.4). При этом должно быть использовано соотношение (1.156).

Найдем условие, при котором

60