Пименов Ю.В., Муравцов А.Д. Техническая электродинамика, 2000

5.7. ЭКВИВАЛЕНТНЫЕ ИСТОЧНИКИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

При анализе конкретных излучающих систем часто возникают ситуации, когда распределение токов в системе либо неизвестно, либо имеет крайне сложный характер, но зато можно считать известным поле на некоторой замкнутой поверхности, охватывающей излучающую систему. В этих случаях поле, излучаемое системой, можно найти непосредственно по значениям векторов Ё и Н на этой поверхности.

Задача формулируется следующим образом. Пусть источники сосредоточены в ограниченной области V. Характер источников и их расположение неизвестны, но зато известны значения векторов Ё и Н на внешней по отношению к источникам стороне поверхности S, ограничивающей объем V. Поверхность S может быть как действительной поверхностью раздела различных сред, так и воображаемой, важно только, что на ней задано поле Ё,Н. Требуется найти поле вне области V. В силу теоремы единственности задача имеет единственное решение.

Среду, расположенную с внешней стороны поверхности S, будем называть первой средой,

а внутри S- второй. Они характеризуются параметрами соответственно. Поля обозначаются аналогично: в первой среде-Ё 1Н1, во второй-

Е2,Н2.

Предположим, что на S отсутствуют поверхностные токи и заряды. Тогда на S должны выполняться следующие условия:

поверхности S.

Для решения задачи применим искусственный прием. Предположим, что поле в облачи V отсутствует. Это заведомо неверное предположение. Однако если значения касательных составляющих векторов Ё и Н на внешней по отношению к V стороне поверхности S останутся прежними, то полученное с помощью такого предположения решение будет

правильным вне области V. Так как при сделанном предположении , то при прежних значениях не будут выполняться граничные условия (5.24)-(5.27). Для

того чтобы на поверхности S векторы остались прежними и в то же время удовлетворяли граничным условиям, предположим, что на S распределены дополнительные источники (поверхностные заряды и токи), компенсирующие образовавшиеся разрывы составляющих векторов Ё и Н. Рассмотрим вначале нормальную компоненту вектора Ё. Если на S имеются

поверхностные электрические заряды с плотностью PSSKB. TO вместо условия (5.24)

должно выполняться условие, аналогичное (1.86): . Так

как по предположению , то искомая ПЛОТНОСТЬ эквивалентных поверхностных зарядов

131

Аналогично компенсируется разрыв касательной составляющей вектора Н. При наличии поверхностных электрических токов с плотностью js экв на S вместо условия (5.27) должно

соотношении , получаем

Разрывы касательной составляющей вектора Ё и нормальной составляющей вектора В = μН можно компенсировать, введя эквивалентные поверхностные магнитные токи и

заряды с плотностями соответственно. При этом соотношения (5.25) и (5.26) следует заменить условиями, подобными (1.98) и (1.86) соответственно. Учитывая, что поле Ё2,Н2 считается равным нулю, приходим к равенствам

Подчеркнем еще раз: предполагается, что в природе нет свободных магнитных зарядов и токов. Их вводят формально для упрощения анализа. В рассматриваемом случае на S вообще может не быть источников, при этом фиктивными будут не только магнитные, но и электрические токи и заряды. Они были введены лишь для того, чтобы при произвольно сделанном предположении об отсутствии поля в области V, где находятся реальные источники, на внешней стороне поверхности S сохранились прежние

значения векторов Ё и Н. При этом в силу теоремы единственности поле в рассматриваемой области не изменится. В тех случаях, когда поверхность S совпадает (полностью или частично) с поверхностью идеального проводника, формулы (5.29) и (5.28) определяют на S (или на части поверхности S) реальные токи и заряды.

Электрические и магнитные поверхностные заряды и токи, определяемые соотношениями (5.28)-(5.31), называют эквивалентными источниками электромагнитного поля, а возможность перехода от значений векторов Е и Н на поверхности S к эквивалентным источникам-принципом эквивалентности (теоремой эквивалентности).

Зная распределение эквивалентных источников, можно найти создаваемое ими электромагнитное поле, например, с помощью векторных электродинамических

потенциалов которые были рассмотрены в 2.4. Векторный потенциал Аm в данном случае определяется выражением (2.61), в котором нужно только заменить

Магнитный векторный потенциал вычисляется по аналогичной формуле, вытекающей из (2.61) и перестановочной двойственности уравнений Максвелла:

где N и М-точки наблюдения и интегрирования соответственно, а R - расстояние от точки М до N.

Поле, созданное эквивалентными источниками, выражается через векторные потенциалы

формулами (2.70).

ПЛОТНОСТИ эквивалентных поверхностных токов и зарядов связаны между собой уравнениями непрерывности, которые в случае монохроматического поля имеют вид:

132

электромагнитное поле однозначно определяется электрическими и магнитными токами, т.е. одними касательными составляющими векторов

Ё и Н на поверхности S. Напомним, что для единственности решения рассматриваемой задачи (см.2.2) достаточно задать на поверхности S либо Ёτ, либо Нτ. Поэтому

одновременное произвольное задание и недопустимо.

5.8. ЭЛЕМЕНТ ГЮЙГЕНСА 5.8.1. Принцип Гюйгенса

Гюйгенсом было сформулировано предположение, согласно которому каждая точка фронта волны, созданной каким-либо первичным источником, является вторичным источником сферической волны. Это предположение называют принципом Гюйгенса.

Под фронтом волны обычно понимают поверхность, отделяющую область, в которой в данный момент времени уже имеют место электромагнитные колебания, от области, в которую волна еще не успела распространиться. При описании распространяющихся монохроматических электромагнитных волн часто вместо термина поверхность равных фаз используют термин фронт волны, что, строго говоря, не совсем корректно.

Пусть известна поверхность Si (рис. 5.24), на которой фаза функции, характеризующей волну, в момент t=t0 равна некоторому значению ψ0. В следующий момент времени t = t0 + ∆t поверхность, соответствующая значению фазы ψ0., уже не будет совпадать с S1. Для определения этой новой поверхности согласно принципу Гюйгенса нужно каждую точку поверхности S1 принять за центр сферы радиуса r0 = c∆t, где с-скорость распространения волны. Тогда поверхность S2 (рис. 5.24), огибающая семейство построенных таким образом сфер, проведенная-с учетом направления распространения волны, будет искомой поверхностью, на которой фаза в момент t = to + +At равна ψ0.

Принцип Гюйгенса справедлив для любых волновых процессов и позволяет проследить за перемещением фронта волны или поверхности равных фаз, начиная с момента времени, в который являются известными фронт волны, или соответственно ПРФ. Математическая формулировка принципа Гюйгенса впервые была дана Кирхгофом. Поэтому указанный принцип обычно называют принципом Гюйгенса-Кирхгофа.

Принцип Гюйгенса-Кирхгофа позволяет находить поле и в том случае, когда поверхность, окружающая источники, не совпадает с поверхностью равных фаз. При этом, конечно, необходимо учитывать распределение фаз эквивалентных источников.

Принцип Гюйгенса-Кирхгофа широко применяется при расчете диаграмм направленности различных излучающих систем СВЧ диапазона. Основные типы антенн этого диапазона: щелевые, рупорные и зеркальные (схематически изображенные на рис. 5.25, а,б,в соответственно) можно представить в виде замкнутой поверхности; одна часть которой (So) является металлической, а другая (SΣ) представляет собой поверхность раскрыва (через нее электромагнитная энергия излучается в окружающее пространство)., Поле йа SΣ обычно известно с той или иной степенью точности, и его можно заменить распределением эквивалентных источников. Поверхности So можно считать идеально

проводящей, тогда , что соответствует отсутствию магнитных токов

133

. Кроме того, при приближенных расчетах часто пренебрегают затеканием электрических токов на внешнюю поверхность антенны, т.е. предполагают, что на поверхности S0 отсутствуют

также электрические токи В таком приближении поле в дальней зоне определяется только эквивалентными

поверхностными электрическими и магнитными токами или, что то же самое, касательными составляющими векторов, Ё и Н на поверхности SΣ.

При вычислении поля можно воспользоваться принципом суперпозиции: разбить поверхность SΣ на элементарные площадки ∆S, найти поле, создаваемое эквивалентными токами каждой площадки, а затем просуммировать полученные результаты.

5.8.2. Поле элемента Гюйгенса

Практически элемент Гюйгенса можно представить как элемент фронта (или ПРФ) распространяющейся волны. Магнитное поле, действующее на этом элементе,

можно заменить эквивалентным электрическим током, а электрическое поле-эквива- лентным магнитным током. Таким образом, элемент Гюйгенса можно рассматривать как элементарный излучатель, обтекаемый электрическими и магнитными токами. Определим его направленные свойства.

Так как векторы Е и Н свободно распространяющейся волны взаимно перпендикулярны, то эквивалентные им электрические и магнитные токи также будут взаимно перпендикулярны. Расположим прямоугольный элемент Гюйгенса (плоскую прямоугольную площадку ∆S = l1l 2) в плоскости ХОΥ так, чтобы начало координат совпадало с его центром. Ориентация касательных составляющих векторов Е и Н на площадке ∆S, соответствующая некоторому моменту времени t0, показана на рис. 5.26, а ориентация электрических и магнитных токов, эквивалентных этим составляющим, в тот же момент времени t0 - на рис. 5.27.

Полагая , получаем, что комплекс-

ные амплитуды эквивалентных электрического 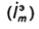и магнитного

токов, текущих по ∆S, равны

Поле, создаваемое элементом Гюйгенса, равно сумме полей, создаваемых расположенными перпендикулярно друг другу элементарным электрическим вибратором

длиной l2 с током i3т и элементарным магнитным вибратором длиной l1 с током . Вычислим поле элемента Гюйгенса в дальней зоне. Рассмотрим, например, плоскость YOZ

134

(плоскость E). Комплексная амплитуда напряженности электрического поля, создаваемого ЭЭВ, в системе

координат, полярная ось которой совпадает с осью У, определяется выражением

где θ1° - координатный орт угла θ1отсчитываемого от оси Υ (рис. 5.28). Соответственно комплексная амплитуда напряженности электрического поля, создаваемого элементарным магнитным вибратором, в рассматриваемой плоскости в системе координат, полярная ось которой совпадает с осью X, равна

где φ20 - координатный орт угла φ2, отсчитываемого от плоскости XOY (рис. 5.29). В верхней части рассматриваемой плоскости (при z > 0) орты θ1° и φ20 совпадают, а в нижней (при z < 0) –то в направлены противоположно. Если можно считать, что

то в направлении оси Z вектор напряженности полного электрического

поля а в противоположном направлении (при φ2 = Зπ/2) Ёт = 0. Вдоль оси Υ (т.е. при φ2 = 0 и φ2 = π) ЭЭВ не излучает, и Ёт = Ё2т. При сделанном предположении диаграмма направленности элемента Гюйгенса в рассматриваемой плоскости (х = 0) имеет вид кардиоиды (рис. 5.30). Обычно поле элемента Гюйгенса записывают в системе координат r, θ, φ, показанной на рис. 5.26. Переходя в формулах

(5.33) и (5.34) от единичных векторов к орту θ0 и от угла θ1 к углу 0 (см. рис. 5.28 и 5.29), получаем следующее выражение для вектора Ёт = Ё1т + Ё2т в плоскости х = 0:

где знак «-» соответствует положительным значениям координаты Υ а знак «+»- отрицательным.

Нетрудно показать, что в произвольном направлении, характеризуемом координатами θи φ, комплексная амплитуда напряженности Электрического поля, создаваемого элементом Гюйгенса, имеет две составляющие:

135

Из формул (5.36) видно, что при выполнении условия диаграмма направленности элемента Гюйгенса одинакова во всех плоскостях, проходящих через ось Z, и имеет вид кардиоиды (см. рис. 5.30). Пространственная диаграмма направленности элемента Гюйгенса представляет собой поверхность, образующуюся при вращении кардиоиды вокруг ее оси симметрии (оси Z). Из диаграммы направленности видно, что излучение максимально в направлением оси Z, перпендикулярной к площадке ∆S.

Вектор напряженности магнитного поля, создаваемого элементом Гюйгенса, в дальней

зоне при любых значениях углов θ и φ можно найти по формуле где г0- орт радиуса-вектора, проведенного из середины элемента Гюйгенса в точку наблюдения. Переходя к составляющим Нθт и Hφm, получаем

5.9. Лемма Лоренца. Теорема взаимности

Пусть в линейной изотропной среде имеются две независимые группы источников, одна

136

Равенство (5.44) называют леммой Лоренца.

На основе леммы Лоренца доказывается теорема взаимности, имеющая фундаментальное значение. Предположим, что источники первой группы

сосредоточены в конечном объеме V1 а источники второй группы -в конечном объеме V2. Области Vi и V2 пространственно разделены (не пересекаются

друг с другом).

Интегрируя равенство (5.44) по произвольной области V, включающей в себя V1 и V2 (рис. 5.31), и применяя теорему Остроградского-Гаусса, получаем

где S - поверхность, ограничивающая объем V.

Соотношение (5.45) является интегральной формулировкой леммы Лоренца.

Распространим интегрирование в уравнении (5.45) на все пространство. При этом поверхность S уйдет в бесконечность. Не нарушая общностисти рассуждений, можно считать, что амплитуды векторов Ё1Н1, Ё2 и Н2 убывают с увеличением расстояния от источников быстрее, чем 1/r (см. теорему единственности, доказанную в 2.2). Тогда при r→∞ левая часть уравнения (5.45) обратится в нуль. Учитывая, кроме того, что по

137

предположению вектор плотности сторонних токов отличен от нуля только в объеме

Vb а вектор -только в объеме V2, получаем

В полученном выражении Ё1, - вектор напряженности электрического поля, создаваемого

в точках объема V2 токами распределенными в объеме V1 a E2- напряженность электрического поля, создаваемого в точках объема V1 токами, протекающими в объеме

V2.

Соотношение (5.46) является одной из наиболее общих математических формулировок

теоремы взаимности.

Выясним некоторые следствия, вытекающие из этой теоремы. Предположим, что объемы

V1 и V2 и распределение токов в них совершенно одинаковы. Из равенства (5.44) следует, что в этом случае векторы Ё1 и Ё2 также будут одинаковыми. Например, пусть имеются две одинаковые антенны 1 и 2 с одинаковым, распределением токов. Тогда вне зависимости от того, является ли разделяющее антенны пространство однородным или неоднородным, можно утверждать, что антенна 1 создает у антенны 2 такое же поле, какое антенна 2 создает у антенны 1.

На основе теоремы взаимности можно также доказать, что диаграмма направленности приемной антенны имеет такую же форму, какую она имела бы, если бы антенна работала в качестве передающей. Применение теоремы взаимности в ряде случаев позволяет существенно упростить решение электродинамических задач.

При доказательстве теоремы взаимности предполагалось, что среда, заполняющая рассматриваемое пространство, является линейной и изотропной. Предположим теперь, что среда, оставаясь линейной, является анизотропной. В этом случае параметры ε и μ (оба или по крайней мере один из них) будут тензорами.

Тогда вместо уравнения (5.44) получаем

138

Глава 6 ПЛОСКИЕ ВОЛНЫ

6.1. ПЛОСКИЕ ВОЛНЫ В ОДНОРОДНОЙ ИЗОТРОПНОЙ СРЕДЕ 6.1.1. Переход от сферической волны к плоской

Рассмотрим еще раз электромагнитное поле, создаваемое ЭЭВ в дальней зоне в безграничной однородной изотропной среде без потерь. Предположим, что векторы Е и Н требуется знать только в области V, размеры которой малы по сравнению с расстоянием до источника (r0). Введем дёкартову систему координат х, у, z, ось Z которой проведена

.вдоль радиуса-вектора, соединяющего середину вибратора Q с точкой О, принятой за начало координат (рис.6.1). В пределах области V можно пренебречь изменением амплитуд векторов Ёт и Нт -и, кроме того, считать, что их фазы зависят только от координаты z, т.е. считать, что sin θ/r= = const, a exp(-ikr)=exp[-ik(ro+z)]. Вводя

обозначение (2λr0) =E0 перепишем формулы (5.20) в виде

В (6.1) учтено, что векторы Ёт и Нт перпендикулярны друг другу и направлению распространения волны (оси Z). Ориентация векторов Ёт и Нт относительно осей X и У зависит от ориентации вибратора, создающего поле. В общем случае эти векторы могут иметь как х-ю, так и у-ю составляющие, связанные соотношениями

Поверхности равных фаз (ПРФ) в данном случае определяются уравнением z = const, т.е. представляют собой плоскости, перпендикулярные оси Z. Волну, ПРФ которой образуют семейство параллельных плоскостей, называют плоской волной. Таким образом, сферическую волну, создаваемую ЭЭВ, в пределах области V можно рассматривать как плоскую волну.

Очевидно, аналогичный результат получится и в тех случаях, когда источником поля являются элементарный магнитный вибратор, элемент Гюйгенса, система таких излучателей и др. При этом в общем случае между составляющими вектора Ёо по осям X и У может иметь место фазовый сдвиг.

6.1.2. Свойства плоской волны в однородной изотропной среде

Исследуем основные свойства плоской волны, распространяющейся в безграничной однородной изотропной среде. Источники, создающие волну, находятся за пределами рассматриваемой области. Поэтому векторы Ёт и Нт удовлетворяют однородным уравнениям Гельмгольца (2.33) и (2.34) соответственно. Предположим, что поле не зависит от координат х и у. Тогда уравнения (2.33) и (2.34) принимают вид

139

Рассматривая таким же образом фазу напряженности электрического поля волны 2), придем к равенству ω∆t=-β∆z. В этом случае положительным ∆t соответствуют отрицательные значения ∆z, то есть волна 2) распространяется противоположно оси Z.

Предположим, что источник, создающий электромагнитное поле, расположен со стороны отрицательных значений z (рис. 6.1). Так как среда считается безграничной и однородной, в рассматриваемой области пространства должна существовать только волна,

140