Пименов Ю.В., Муравцов А.Д. Техническая электродинамика, 2000

Перейдем от векторного потенциала А к напряженности магнитного поля Н. Предполагая, что пространство заполнено однородной изотропной средой, получаем

Учитывая, что плотность тока j не зависит от координат точки, в которой вычисляется поле, и используя тождество rot(ψ,a)-= ψ rot a + [grad ψ, а], преобразуем подынтегральное выражение в (4.15):

где R0 = R/R-opт вектора R, проведенного из dV в точку наблюдения. Подставляя (4.16) в (4.15), получаем

К аналогичным выражениям для вектора Н приводят формулы 4.13) и (4.14) в случае поверхностных и линейных токов:

Соотношения (4.17)-(4.19) представляют собой интегральные формы закона Био-Савара:

Закон Био-Савара характеризует магнитное поле dH, создаваемое элементом тока Idl. Связь формул (4.19) и (4.20) очевидна. Покажем, что поля, определяемые выражениями (4.17) и (4.18), также можно представить в виде суперпозиции элементарных полей dH, определяемых соотношением (4.20), от отдельных элементарных токов. Преобразуем подынтегральное выражение в (4.17). Выберем в качестве элемента dV элемент токовой трубки . длиной dl, ось которой, направлена по току, а сечение равно dS. Обозначив через /=jdS полный ток, протекающий по трубке, и учитывая множитель 1/4π перед интегралом, получим выражение ;

полностью совпадающее с правой частью формулы (4.20). Связь формул (4.18) и (4.20) доказывается аналогично.

Часто при решении практических задач для упрощения расчета предполагается, что ток вдоль одной из координатных осей остается неизменным, т.е. что линии тока по этой координате уходят в бесконечность. Такие предположения обычно делаются при определении поля, создаваемого линейным током, который протекает вдоль длинной нити, или токами, протекающими вдоль длинного цилиндра. Предположение о бесконечной протяженности линий тока не позволяет использовать формулы (4.17)-(4.19). Рассмотрим эти особые случаи.

Найдем магнитное поле и векторный потенциал прямолинейной бесконечно-протяженной уединенной нити, обтекаемой постоянным током. Пусть эта нить совпадает с осью Z цилиндрической системы координат. Очевидно, что напряженность магнитного поля Н в

101

этом случае имеет одну составляющую Нφ и не зависит от переменных z и φ. Выбирая в качестве контура Г в (4.1) окружность радиуса r, лежащую в плоскости, перпендикулярной к оси Z, получаем напряженность магнитного поля нити

За направление тока в (4.21) принято направление оси Z.

Векторный потенциал рассматриваемой нити должен иметь только z-ю составляющую (A=zoA), величина которой зависит от координаты r. Учитывая (4.10) и расписывая rot А в цилиндрической системе координат, получаем

, откуда следует, что

Интегрируя выражение (4.22) по г, находим

Постоянную С в формуле (4.23) обычно полагают равной нулю. Тогда

От формулы (4.24) нетрудно перейти к выражению для потенциала, создаваемого токами, неизменными вдоль оси Z, которые протекают по цилиндру произвольного сечения S:

где - расстояние от элемента dS, характеризуемого координатами ξ; η, До точки наблюдения N(х;у), dS = dξ,dη (см. рис. 3.5).

Если поле создано поверхностными токами, распределенными по некоторой цилиндрической поверхности S, образующие которой параллельны оси Z, а плотность поверхностных токов не зависит от координаты z, то векторный потенциал А выражается формулой

где Г-линия пересечения поверхности S с плоскостью, перпендикулярной к оси Z, a R- расстояние от элемента dl до точки N, в которой вычисляется потенциал (см. рис. 3.6).

4.4. ЭНЕРГИЯ СТАЦИОНАРНОГО МАГНИТНОГО ПОЛЯ

Общее (1.132) выражение для энергии магнитного поля, сосредоточенной в некотором объеме V, остается справедливым и в случае стационарных процессов:

Формулу (4.27) можно преобразовать таким образом, чтобы магнитная энергия была выражена через токи, создающие магнитное поле. Для этого заменим в (4.27) вектор В его представлением через векторный потенциал А. Используя тождество НВ = Н rot A = div [А, Н] + A rot H, получаем

102

Первый интеграл в уравнении (4.28) преобразуем в поверхностный интеграл, используя теорему Остроградского-Гаусса, а во втором интеграле выразим rot H через плотность токов j с помощью равенства rot Н = j. Тогда соотношение (4.28) примет вид

где S-поверхность, ограничивающая объем V.

Выберем в качестве поверхности S сферу радиуса r и устремим r к бесконечности, т.е. распространим интегрирование в (4.29) на все пространство.

Любая пространственно ограниченная система токов, как следует из формул (4.12)-(4.14) и (4.17)-(4.19), создает магнитное поле, напряженность Н и векторный потенциал А которого при r→∞ убывают пропорционально 1/r2 и 1/r соответственно (или еще быстрее). При этом поверхность S возрастает пропорционально r2. Следовательно, в пределе при r→∞ первый интеграл в правой части уравнения (4.29) будет равен нулю. В результате получим

Вотличие от исходного выражения (4.27) интегрирование в (4.30) распространяется лишь

на ту область пространства Vo, в которой имеются токи. В формуле (4.30) можно исключить векторный потенциал А. Для этого нужно заменить вектор А его представлением в виде интеграла (4.12).

Вслучае линейных токов выражение для энергии магнитного поля упрощается. Рассмотрим вначале уединенный контур Г с током /. Формула (4.30) для этого контура принимает вид

Применим к интегралу в (4.31) теорему Стокса:

где Ф-магнитный поток через поверхность S, опирающуюся на контур Г. Подставляя

(4.32) в (4.31), получаем

В случае N контуров (Г1,Г2,...,ГN) выражение для WM записывается следующим образом:

где Фn-магнитный поток, сцепленный с контуром Гn a /n-ток в контуре Гn.

В формуле (4.34) векторный потенциал А и поток Фn обусловлены не только током /n но и токами в остальных контурах. В силу принципа суперпозиции можно записать следующее равенство:

где Аk- векторный потенциал, создаваемый в рассматриваемой точке током 1к, протекающим в контуре Гk.

Выделим в сумме (4.35) векторный потенциал Аn соответствующий току 1п:

103

и подставим (4.36) в (4.34). В результате придем к выражению

Преобразовав интегралы в полученном выражении с помощью теоремы Стокса, перепишем его в виде

где Фnk -поток, сцепленный с контуром Гn который обусловлен током 1к контура Гk. Первое слагаемое в правой части формулы (4.37) определяет собственную энергию контуров системы, а второе -взаимную энергию.

4.5. ИНДУКТИВНОСТЬ

Поток Ф, пронизывающий уединенный контур Г, пропорционален току в этом контуре:

Ф = LI. (4.38)

Коэффициент L зависит от конфигурации и размеров контура Г и называется его индуктивностью. Индуктивность измеряется в генри (Гн). Из закона индукции Фарадея (1.34) и формулы (4.38) следует, что индуктивность уединенного контура численно равна величине эдс, наводимой в этом контуре при линейном изменении его тока на 1 А за 1 с.

Подставляя (4.38) в (4.33), получаем

WM = L12I2. (4.39)

В случае N контуров поток Фпk пропорционален току 1к:

Фпк=МпкIк. (4.40)

Коэффициент пропорциональности Мпk при к≠п называют взаимной индуктивностью контуров Гk и Гn а коэффициент Мkk=Lk-собственной индуктивностью контура Гk. Коэффициент Мпk при к≠п можно определить следующим образом. Воспользовавшись формулами (4.32) и (4.14), представим выражение для потока Фпk в виде

где dln и dlk-элементы контуров Гn и Гk соответственно, a R-расстояние между этими элементами.

Приравнивая правые части формул (4.41) и (4.40), получаем

Как видно, взаимная индуктивность контуров Гn и Гk зависит только от их формы и взаимного расположения и не изменяется при перестановке индексов (свойство взаимности):

Из закона индукции Фарадея (1.34) и формулы (4.40) следует, что взаимная индуктивность двух контуров численно равна эдс, наводимой в одном из них при линейном изменении тока в другом на 1 А за 1 с.

Для определения собственной индуктивности контура выражение (4.42) непригодно. Обычно вместо него используют соотношения (4.38) и (4.39).

Перепишем выражение для энергии магнитного поля системы линейных токов (4.37) с учетом равенства (4.40):

104

Таким образом, для определения энергии магнитного поля системы линейных токов достаточно знать собственные и взаимные индуктивности контуров и токи в них.

4.6. ПРИМЕРЫ РАСЧЕТА МАГНИТНЫХ ПОЛЕЙ Поле бесконечно длинного проводника. Вычислим магнитное поле бесконечно

длинного цилиндрического проводника радиуса а. Будем считать для простоты, что ток / распределен равномерно по сечению проводника. Введем цилиндрическую систему координат r,φ, z, ось Z которой совпадает с осью проводника. Ввиду симметрии задачи поле не зависит от угла φ. Поле также не зависит от z, поэтому для определения вектора Н можно использовать закон Ампера (первое уравнение в (4.1)).

Выбирая в качестве контура Г окружность радиуса r≥a, лежащую в плоскости, перпендикулярной к оси Z с центром на оси Z, получаем

Для определения магнитного поля внутри провода выберем в качестве контура Г окружность радиуса r<a. Учитывая, что ток, охватываемый контуром Г, в этом случае равен 1(r/а)2, получаем

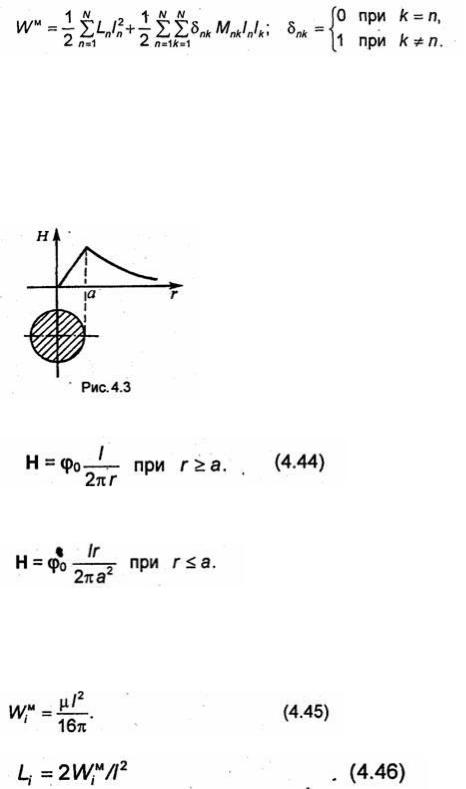
Таким образом, поле цилиндрического проводника в области 0≤ r ≤ a линейно возрастает от нуля до некоторого максимального значения (рис. 4.3), равногоI /(2πa), а при r≥а совпадает с полем прямолинейного тока величиной /, определяемого формулой (4.21).

Вычислим энергию магнитного поля сосредоточенного внутри проводника на участке единичной длины. Используя (4.27) и выражение (4.44), получаем

По аналогии с формулой (4.39) величину

называют внутренней индуктивностью на единицу длины цилиндрического проводника.

Из формул (4.45) и (4.46) получаем

105

Таким образом, внутренняя индуктивность на единицу длины цилиндрического проводника при равномерном распределении тока по его сечению не зависит от диаметра проводника.

Поле коаксиального кабеля. Пусть ток, протекающий по внутреннему проводу коаксиального кабеля (рис. 4.4), равен /, а ток внешнего проводника -/. Распределение тока по сечениям проводников будем считать равномерным. Поступая так же, как и в случае уединенного проводника, придем к следующим выражениям для напряженности магнитного поля:

Радиусы проводников а1,а2 и а3 указаны на рис. 4.4. Там же приведена кривая, характеризующая зависимость напряженности магнитного поля коаксиального кабеля от координаты r.

Для вычисления индуктивности L1 на единицу длины коаксиального кабеля представим ее в виде суммы трех слагаемых:

где L’i и L’’i-внутренние индуктивности на единицу длины центрального и наружного проводников соответственно, а Lе-так называемая внешняя индуктивность на единицу длины коаксиального кабеля, определяемая магнитным потоком между проводниками.

Величины L’i и L’’i вычисляются по формуле (4.46). Опуская очевидные преобразования, выпишем окончательные результаты:

где μ- абсолютная магнитная проницаемость проводника. Как видно, внутренняя индуктивность на единицу длины центрального проводника коаксиального кабеля (L’i) совпадает с внутренней индуктивностью на единицу длины уединенного цилиндрического проводника (4.47).

Внешнюю индуктивность Le определим в соответствии с формулой (4.39) следующим образом:

106

где - энергия магнитного поля, сосредоточенного в зазоре между проводниками, приходящаяся на единицу длины коаксиального кабеля. Вычисляя энергию магнитного поля по формуле (4.27):

Предполагается, что магнитная проницаемость среды, заполняющей коаксиальный кабель, равна μ0-

Поле двухпроводной линии. Рассмотрим вначале поле двух линейных противоположно направленных токов / и -/, т.е. токов, протекающих по бесконечно тонким прямолинейным нитям, расположенным на расстоянии 2l друг от друга (рис. 4.5). Магнитные силовые линии лежат в плоскостях, перпендикулярных оси Z, и определяются (см. 1.2.4) уравнением

Векторный потенциал имеет только продольную (параллельную оси Z составляющую и в силу принципа суперпозиции равен сумме потенциалов каждого из токов:

Учитывая равенство (4.10), из уравнения (4.49) получаем соотношение (дA/dx)dx + (dA/dy)dy = 0, которое может быть переписано в виде dA=0, где dA-полный дифференциал функции А. Следовательно, функция А не изменяется вдоль магнитной силовой линии. Это означает, что магнитные силовые линии совпадают с линиями пересечения плоскостей, перпендикулярных оси Z, с поверхностями, на которых А = const. Эти поверхности определяются из условия R2/R1 = b = const, которое совпадает с уравнением (3.50), определяющим эквипотенциальные поверхности системы двух параллельных противоположно заряженных нитей. Таким образом, поверхности, на которых величина векторного потенциала постоянна, представляют собой поверхности круговых цилиндров, параллельных оси Z, местоположение осей и радиусы которых определяются формулами (3.52) и (3.53) соответственно, а магнитные линии образуют семейство окружностей, возникающих при пересечении этих цилиндрических поверхностей с плоскостями, перпендикулярными оси Z (рис. 4.6).

107

В реальной двухпроводной линии проводники имеют круговые сечения конечных размеров. Однако, если магнитная проницаемость проводов равна магнитной проницаемости внешней среды, то в случае тонких проводов поле вне проводов практически не отличается от поля линейных токов, совпадающих с геометрическими осями проводов. Поэтому все сказанное применимо и к реальной линии из тонких проводов.

Вычислим индуктивность L1 на единицу длины двухпроводной линии, образованной одинаковыми проводами, расстояние между осями которых (2ft) много больше их диаметров (2а). Величина L1‘=2LI‘ + Le, где Lе- внешняя индуктивность двухпроводной линии на единицу длины. Значение L1‘ вычисляется по формуле (4.47). Для определения Le воспользуемся формулой (4.38). Вычислим магнитный поток Ф через поверхность, охватываемую контуром ABCD, расположенным в плоскости у=0 (рис.4.7). Стороны АВ и CD параллельны оси Z, имеют единичную длину и лежат на поверхности проводов (х = h - а на АВ и х = а - h на CD).

В рассматриваемом случае векторный потенциал А определяется выражением (4.50), в котором нужно только заменить l на h. Так как В = rot А, то

Интегрируя (4.51) по площади SABCD, ограниченной контуром А имеем

ABCD, имеем

Следовательно, внешняя индуктивность двухпроводной линии на единицу длины

108

Если абсолютные магнитные проницаемости проводов и окружающей среды равны |д0, то полная погонная индуктивность двухпроводной линии в случае тонких проводов (h>>а) равна

Поле кругового контура, обтекаемого постоянным электрическим током. Вычислим поле линейного тока /, образующего круговой виток радиуса а (рис. 4.8). Введем сферическую систему координат r, θ, φ, полярная ось которой совпадает с осью витка, а начало-с его центром. Так как рассматриваемое поле должно быть осесимметричным, то начало отсчета угла φ можно выбрать произвольно. Будем отсчитывать его от плоскости, проходящей чер полярную ось и точку наблюдения N( r, θ,0), в которой вычисляется поле. Для определения векторного потенциала воспользуемся выражением (4.14). Проецируя вектор dl на направления r0,θ0, φо, соответствующие точке наблюдения N(r, θ ,0), получаем

-полные эллиптические интегралы первого и второго рода соответственно.

109

Эллиптические интегралы не выражаются через элементарные функции, однако они подробно изучены, и имеются таблицы их значений в зависимости от величины b, называемой модулем этих интегралов.

Для вычисления вектора Н воспользуемся соотношением (4.10). Выражение для rot А в сферической системе координат определяется формулой (П. 17), приведенной в приложении 4. Так как векторный потенциал А имеет одну составляющую А=φ0А не зависящую от угла φ, из формулы (П. 17) следует, что напряженность магнитного поля имеет две составляющие:

При дифференцировании полных эллиптических интегралов К(b) и E(b), входящих в формулу (4.55), удобно пользоваться формулами

где ралов.

Отметим, что выведенные формулы можно использовать и в случае кольцевого проводника конечной толщины, если радиус витка и расстояние до точки, в которой вычисляется поле, велики по сравнению с поперечными размерами сечения проводника.

Поле магнитного диполя. Рассмотрим поле кругового витка, считая, что точки наблюдения находятся на больших по сравнению

с радиусом витка расстояниях от его центра (r>>а). В этом случае выражение для векторного потенциала (4.54) существенно упрощается. Разложим входящую под знак интеграла величину 1/R в ряд по степеням отношения air и пренебрежем членами порядка (a/r)2 по сравнению с единицей:

Напряженность магнитного поля имеет две составляющие Нr и Нθ, определяемые соотношениями (4.56). Выполняя дифференцирование, получаем

перепишем формулу (4.60) в виде

В области, где справедливо равенство (4.62), плотность тока проводимости равна нулю (j = 0), а любой принадлежащий ей контур не охватывает тока, т.е. выполняются уравнения (1.56). Следовательно, поле, определяемое формулой (4.62), можно считать

110