Komyak_A_I_Molekulyarnaya_spektroskopia

ni n0

4

3

2

1

0

Рис. 2.7. Относительная заселенность вращательных уровней молекулы HCl (Т = 300 К)

Значение J для максимума интенсивности можно приближенно оценить, если продифференцировать выражение (2.21) по J. Приравняв dni/dJ к нулю, получим:

Учитывая, что для комнатной температуры kТ 208,6 см–1 , а для

HCl kТ = 10,59 см–1 то получим Jmax 3, т. е. функция (2.21) имеет максимум при J равном трем. Для более тяжелых молекул, у которых Be

достаточно мало (например, F2) максимум заселенности уровня при одной и той же температуре приходится на большее J (для молекулы F2

Jmax 10).

Если совокупность молекул содержит различные изотопы (например, молекулы С12О16 и С13О16 ), то их вращательные спектры будут слегка отличаться, так как у более тяжелого изотопа Be . будет меньше и спектр

молекулы С13О16 располагаеться со стороны меньших частот. Измеряя положение линий с большой точностью, можно вычислить равновесное расстояние re между атомами в молекуле. С другой стороны, если оно известно из рентгеноструктурных или нейтронографических измерений, то, имея вращательные спектры, можно определить массу изотопа. Если дополнительно измерять интенсивность линий вращательного спектра, то можно определить относительное содержание изотопного вещества.

63

До настоящего времени рассматривали двухатомную молекулу как жесткое образование и пренебрегали возможными изменениями межъядерного расстояния. В действительности, если отвлечься от колебаний, при увеличении вращения будет изменяться межъядерное расстояние молекулы за счет центробежных сил вращения. При этом, чем интенсивнее вращение, тем больше центробежные силы будут растягивать молекулу. Это приведет к увеличению момента инерции Ie и к уменьшению вращательной постоянной Ве. В энергетическом спектре жесткого ротатора совокупность уровней энергии представляла собой расходящуюся последовательность. Для нежесткого ротатора эта последовательность будет сходящейся. Аналитическое выражение для вращательной энергии нежесткого ротатора имеет следующий вид:

где D – постоянная центробежного растяжения, которая всегда положительна и по порядку величины равна 10–6 см–1 (для молекулы водорода она несколько больше). Это величина мала по сравнению с Be .

При малых J поправочным членом D J2(J + 1)2 можно пренебречь, но начиная со значений J 10 его уже необходимо учитывать. Правила отбора для нежесткого ротатора остаются такими же, как и для жесткого. В табл 2.2 для ряда двухатомных молекул приведены вращательные постоянные Be и межъядерные расстояния re , полученные из

вращательных спектров.

2.3. ВРАЩАТЕЛЬНЫЕ СПЕКТРЫ МНОГОАТОМНЫХ МОЛЕКУЛ

2.3.1.Деление молекул на сферические, симметричные

иасимметричные волчки

Если многоатомную молекулу, атомы которой не располагаются на одной прямой, рассматривать как твердое тело (жесткий ротатор), то вращение его может быть весьма сложным. Это вращение разлагают обычно по трем взаимно перпендикулярным направлениям – главным осям вращения, которые пересекаются в центре масс молекулы. Моменты инерции вокруг трех взаимно перпендикулярных осей вращения могут быть представлены с помощью эллипсоида инерции, ориентация которого фиксирована в молекуле, а центр масс молекулы совпадает с центром эллипсоида инерции. Каждый эллипсоид имеет три взаимно перпендикулярные главные оси. Если выбрать систему

64

координат так, чтобы оси X , Y, Z совпадали с главными осями эллипсоида инерции, то уравнение эллипсоида инерции может быть записано в виде

называемые главными моментами инерции. Многоатомная молекула будет обладать тремя главными моментами инерции, которые обозначим

через IА , IВ, и IС.

Вращение любой молекулы можно выразить через ее вращение относительно главных осей инерции. Для рассмотренных выше двухатомных молекул (см. рис. 2.1) эллипсоид инерции является плоским диском, ибо момент инерции относительно оси молекулы равен нулю ( I z 0 ), а два других момента равны друг другу ( I x , – I y ).

Вращающаяся нелинейная несимметричная молекула, у которой все три главных момента инерции различны, называется асимметричным ротатором (асимметричным волчком). Его главные моменты инерции обычно располагаются в порядке их возрастания:

Трем моментам инерции соответствуют три вращательные постоянные, обозначаемые через А, В и С:

Эти постоянные соответствуют равновесной конфигурации молекулы (минимуму потенциальной энергии, значок « е » для постоянных опускаем) и располагаются в порядке их уменьшения

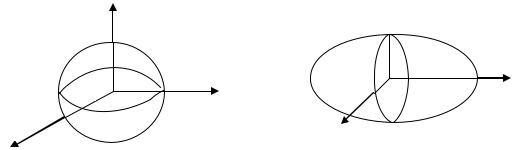
Если в молекуле три главных момента инерции равны (IA= IB = IC),то она относится к сферическому волчку. Этот случай осуществляется для довольно симметричных молекул типа CH4, UF6, CCl4, которые относятся к точечным группам симметрии Td, Oh. В силу высокой симметрии у таких молекул отсутствует постоянный дипольный момент и эллипсоид поляризуемости представляет собой сферу (рис. 2.8). Поэтому указанные молекулы не имеют чисто вращательных спектров поглощения и комбинационного рассеяния. Мы рассмотрели два крайних случая: случай высокосимметричных и несимметричных молекул

65

наименьшего момента инерции (IA) в соответствии с условием (2.25), согласно которому моменты инерции волчков располагаются в по рядке их возрастания.

Таким образом, будем совершать переход от вытянутого волчка к сплюснутому через промежуточный переход асимметричного волчка, для которого А > В > С. Чем меньше отличается В от С или от А, тем ближе асимметричный волчок к симметричному, вытянутому или сплюснутому. В качестве параметра, характеризующего асимметрию волчка, обычно вводят отношение

Для вытянутого симметричного волчка, когда B = C, = –1 для

сплюснутого волчка, когда A = B, = 1. Для асимметричного волчка, у которого В есть среднее между А и С, т. е.

B A C , 2

это отношение обращается в нуль ( = 0). При значениях , близких к –1, получаем слегка асимметричный волчок, близкий к вытянутому симметричному; при близких к +1 получаем слегка асимметричный волчок, близкий к сплюснутому симметричному.

Для многих молекул существенным является не только параметр , но

постоянными А и С. Это отношение может изменяться от 0 до 1. Нуль получаем, если А = С. В соответствии с (2.27) постоянная. В также

67

должна быть равна А или С. Следовательно, мы имеем дело со сферическим волчком, у которого IA = IB = IC. Предельное значение

невозможен так как он соответствует IC = ), что осуществляется для линейных молекул. Таким образом, линейную молекулу можно рассматривать как предельный случай вытянутого симметричного волчка, для которого IA 0.

В случае плоских молекул момент инерции относительно оси IC , перпендикулярной плоскости молекулы (эта ось является одной из

Из соотношения между моментами инерции можно найти соотношения между вращательными постоянными:

т. е. момент инерции относительно оси симметрии сплюснутого волчка равен удвоенному моменту инерции относительно любой перпендикулярной к ней оси. Этот случай реализуется для плоских молекул с выделенной осью симметрии порядка n 3 (например, молекула бензола С6H6 ион NO3– и др.).

2.3.2.Вращательные уровни энергии сферического волчка.

Умолекул типа сферического волчка три главных момента инерции

равны: IA = IB = IC . У них эллипсоид поляризуемости представляет собой сферу и отсутствует дипольный момент, поэтому они не активны в ИК- и КР-спектрах и представляют только теоретический интерес.

Однако имеется одно существенное различие молекул типа сферического волчка от линейных молекул, рассмотренных в п. 2.1, которое заключается в числе вращательных степеней свободы.

68

Последнее будет проявляться в степени вырождения вращательных уровней энергии. Вращательные уровни молекул типа сферического волчка легко можно найти, если записать классическое выражение для энергии вращения молекулы с тремя моментами инерции, отличными от нуля. Это выражение будет иметь вид:

где Px , Py , Pz – составляющие механического момента по подвижным

осям, за которые выбираются главные оси инерции, а IA , IB , IC – соответствующие моменты инерции вокруг этих осей. Учитывая тот факт, что для сферического волчка все три момента инерции равны (IA = IB = IC ), формулу (2.34) можно переписать следующим образом:

где P2 Px2 Py2 Pz2 .

Учитывая затем квантование квадрата момента количества движения, формулу (2.35) перепишем иначе

образом, вращательные уровни молекулы типа сферического волчка определяются той же формулой, что и вращательные уровни двухатомной линейной молекулы. Существенное различие имеется в числе вращательных степеней свободы.

Для характеристики вращательного движения двухатомной молекулы достаточно было двух степеней свободы. Для этого вводились два квантовых числа J и mJ, определяющих значения квадрата момента количества движения и проекции момента количества движения на одну из неподвижных в пространстве координатных осей.

Молекула типа сферического волчка, как и любая нелинейная молекула, будет иметь три вращательные степени свободы. Для полной характеристики ее вращательного движения необходимо задать три квантовых числа. Два ранее названных квантовых числа J и mJ сохраняют свой смысл, а скажем k, будет определять значение проекции момента количества движения на одну из подвижных координатных

69

осей. Направление этих осей может быть выбрано произвольно, т. е., их можно выбрать совпадающими с направлением главных моментов инерции. Необходимо только, чтобы эти оси вращались вместе с молекулой. Проекция момента количества движения на подвижную ось, которую выбирают совпадающей с осью Z, квантуется совершенно так же, как и проекция на неподвижную ось, а именно

где k = J(J – 1), ..., 0 ,...–J + 1, –J, т. е. принимает 2J + 1 значений.

Так как энергия от квантового числа k не зависит, то получается дополнительное вырождение уровней энергии кратности 2J + 1. Это вырождение имеет место наряду с вырождением mJ кратности (2J + 1)2, т. е. вырождение сохраняется относительно проекций момента количества движения на подвижную и неподвижную оси координат. Общая степень вырождения уровней энергии молекул типа сферического волчка по mJ и k равна

Для каждого вращательного числа J возможны 2J + 1 ориентации момента относительно неподвижных и 2J + 1 относительно подвижных осей, что и приводит к (2J + 1)2 возможным состояниям.

Как видим в п. 2.2, число молекул во вращательном состоянии с заданным значением J будет определяться формулой:

Сравнивая формулы с формулой (2.39) и (2.21) видим, что для молекул типа сферического волчка большая их доля будет находиться на высоких вращательных уровнях, чем для линейных молекул с той же вращательной постоянной B и температурой Т. Например, для вращательного уровня J = 4 различие в статистических весах уровней энергии для линейной молекулы и молекулы типа сферического волчка равно 9, а для J = 10 это различие будет более 20. Эти различия принимаются во внимание и особенно существенны при термодинамических расчетах.

Чисто вращательные спектры имеют место лишь у молекул, которые только случайно (а не в силу высокой симметрии) являются сферическими волчками. В этом случае у них дипольный момент не обязательно равен нулю, а эллипсоид поляризуемости не должен быть сферой.

70

2.3.3. Вращательные уровни энергии и спектры молекул типа симметричного волчка

Симметричным волчком будем называть молекулу, в которой равны два главных момента инерции (IВ = IС для вытянутого волчка или IA = IB для сплюснутого волчка). Третий момент инерции не равен нулю и не совпадает с двумя другими. Примером вытянутого симметричного волчка является молекула метилфторида FCH3 , в которой три атома водорода тетраэдрически связаны с атомом углерода, а атом фтора находится на большем расстоянии по сравнению с водородом от атома углерода. Вращение такой молекулы вокруг оси С – F (ось симметрии молекулы) отличается от вращения вокруг двух других осей, перпендикулярных данной. Моменты инерции относительно двух других осей равны IB = IC . Момент инерции относительно направления связи С – F(IA) хотя и мал, но им пренебрегать нельзя. Вклад во вращение вокруг этой оси (она совпадает с осью симметрии молекулы) вносят три атома водорода, расположенных вне этой оси.

Уровни энергии симметричного волчка можно найти через квадраты соответствующих моментов количества движения

Для симметричного вытянутого волчка Ix = Iy, а Iz Iy. Ось Z совпадает

В формуле (2.40) мы добавили и вычли выражение pz2 I y ). В первый

член выражения (2.41) входит квадрат полного момента p2 , который квантуется и равен BJ(J + 1) (см. 2.2), а во второй член входит проекция квадрата момента на ось Z , являющуюся осью симметрии волчка. Проекция момента Рz квантуется и принимает значения Рz = ћk. Таким образом квантованное выражение дли энергии вращения будет иметь вид:

71