Сформулируем задачу. Известно:

1)уравнения состояния (1.1);

2)система ограничений, наложенных на переменные состояния и управляющие воздействия (1.2) и (1.3);

3)граничные условия (начальное x0 и конечное xT состояния ОУ).

Найти такой алгоритм управления u* (t) U , который обеспечивает экстремум некоторому функционалу J = M {F[x(t), x&(t), u(t), t]} → extr , заданному на управлениях u(t) и соответствующим им значениях x(t) X , и переводит ОУ из начального состояния x0 в заданное xT . Здесь x(t) – решение системы (1.1) с начальными условиями x(t0 ) = x0 , соответствующее управлению u* (t).

Для решения задач параметрической оптимизации используют методы математического программирования; для решения задач оптимизации управления – вариационные методы, принцип максимума Понтрягина, динамическое программирование.

Тема 2. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

2.1. Постановка задачи математического программирования. Виды экстремума функций многих переменных

К задачам математического программирования (МП) относятся задачи оп-

тимизации, в которых отыскивается экстремум заданной скалярной функции многих переменных при ограничениях в форме системы равенств и неравенств. Все они с формальной точки зрения могут быть сведены к следующей постановке.

Найти значения переменных x1, x2 ,..., xn , доставляющие экстремальное значения некоторой функции F = F(x1, x2 ,..., xn ) и удовлетворяющие m уравнениям и неравенствам

янные величины. Условия (2.1) называются ограничениями. Как правило, отдельно оговариваются ограничения на знак переменных xi ≥ 0,i =1, n , так как методы

их учета могут быть иными, чем сложных ограничений типа (2.1). Могут налагаться условия целочисленности переменных. Кратко условия задачи МП можно записать следующим образом:

6

min(max){F(x) g j (x)(≤,=,≥)bj , xi ≥ 0,i =1,n; j =1,m}.

Если при определении экстремума ограничиться рассмотрением минимизации, задача не теряет общности, так как максимизация функции F1(x) эквива-

лентна минимизации функции F(x) = −F1(x) , т.е. max F(x) = −min[−F(x)].

Функция F = (x1, x2 ,..., xn ) называется целевой функцией, или функцией це-

ли. Переменные xi , удовлетворяющие совокупности заданных ограничений,

представляют собой допустимое решение задачи, и называются планом задачи. Допустимое решение, доставляющие экстремум функции цели F = F(x1, x2 ,..., xn ) ,

называется оптимальным решением, или оптимальным планом. Не каждая за-

дача математического программирования имеет планы, так как не каждая система ограничений имеет решение.

Основные виды экстремума функций конечного числа переменных.

Пусть F(x) определена в некоторой области R переменных x1, x2 ,..., xn . Если

на переменные не накладывается никаких ограничений, т.е. область R не ограничена, то экстремум функции F(x) называется безусловным, а в противном случае

– условным.

Простейшая задача оптимизации связана с нахождением значений переменных, обеспечивающих экстремум функции цели при отсутствии ограничений, т.е. с нахождением безусловного экстремума функции.

Безусловным глобальным минимумом (максимумом) функции называется наименьшее (наибольшее) в пределах всей рассматриваемой области R значение

этой функции. Если в некоторой точке x = x0 R функция F(x) имеет меньшее (большее) значение, чем во всех точках x , принадлежащих некоторой малой ок-

рестности точки x0 , то говорят, что в этой точке имеет место локальный минимум (максимум) функции F(x) .

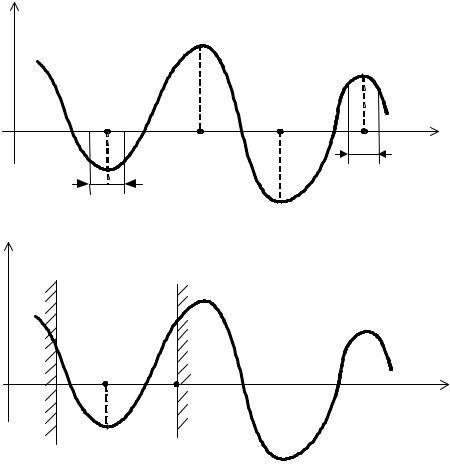
На рис. 2.1, а изображена функция F(x) , заданная на неограниченной облас-

ти R, здесь в точках x1* и x2* достигается соответственно глобальный безусловный максимум и минимум функции F(x) , так как

F(x2* ) ≤ F(x) и F(x1*) ≥ F(x) для x R .

В точках x10 и x20 достигается безусловный локальный минимум и максимум функции F(x) , так как в ε окрестностях этих точек удовлетворяются условия:

F(x10 ) ≤ F(x10 ± ε) , F(x20 ) ≥ F(x20 ± ε) , ε > 0 .

7

Очевидно, что если в пределах области R имеется всего один минимум (максимум), то он является глобальным.

При наличии ограничений область R ограничивается областью допустимых значений переменных X. В этом случае точки экстремума должны обязательно принадлежать области X и сам экстремум называется условным. При этом экстремумы называются граничными, если они имеют место в граничных точках области и внутренними, если соответствуют внутренним точкам области X.

На рис. 2.1, б область X ограничена: X ={x | a ≤ x ≤ b}. Точке x10 здесь будет

соответствовать условный глобальный минимум функции F(x), а точкам x = a и x = b – условный локальный и глобальный максимум соответственно. Причём экстремумы в точках x = a и x = b являются граничными. Для решения практических задач наибольший интерес представляет нахождение глобального условного экстремума.

F(x)

F(x)

б

Рис. 2.1. Примеры экстремума функции одной переменной: а – безусловные; б – условные

8

2.2. Определение выпуклости функций

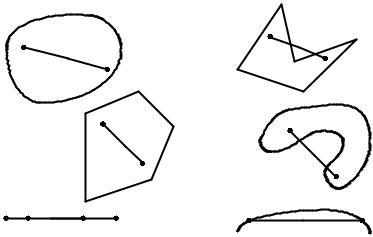
Одним из важнейших понятий, используемых в математическом программировании, является понятие выпуклости. Точечные множества S называются выпуклыми, если для любых двух точек x1 S и x2 S следует, что

[αx1 + (1 − α)x2 ] S , где α [0,1] . Геометрически это означает, что если две точ-

ки принадлежат множеству S, то и весь отрезок, соединяющий эти точки, принадлежит S.

На рис. 2.2, а показано несколько примеров выпуклых, а на рис. 2.2, б – несколько примеров невыпуклых множеств.

Аналогично дается определение выпуклой функции. Функция F(x) является выпуклой на выпуклом множестве S, если для любых двух точек x1, x2 S выполняется соотношение

где α [0,1] .

Рис. 2.2. Примеры выпуклых и невыпуклых множеств: a – выпуклые множества; б – невыпуклые множества

Если в (2.2) знак «≤» можно заменить на знак строгого неравенства « < », то функция F(x) будет строго выпуклой. На рис 2.3 показана геометрическая ин-

терпретация определения выпуклой функции одной переменной, откуда следует, что выпуклая функция F(x) всегда расположена ниже любой прямой, соединяю-

9