Для определения постоянных интегрирования C1 и C2 необходимо

задать начальные условия для функции Ψ(t) . Однако они не могут зада-

tоднозначно определил бы какой-то процесс x(t) из всей совокупности и

x&0 = f0 , а следовательно, и Ψ0 (t) можно не включать в выражение для H, если

функционал не содержит в явном виде управления u, так как в этом случае слагаемое Ψ0 f0 не влияет на максимизацию H.

7.3.3. Принцип максимума в задачах о максимальном быстродействии. В

задачах о максимальном быстродействии минимизируемый функционал характеризует время перехода системы из состояния x(t0 ) в состояние x(t1) и имеет вид

афункция f0 (x,u) ≡1.

Сучётом (7.55) составим функцию H1 , равную

n

H1 = Ψ0 + ∑Ψi fi (x,u) . (7.56)

i =1

139

С учётом сказанного, принцип максимума для систем, оптимальных по быстродействию формулируется следующим образом.

Для оптимальности системы по быстродействию необходимо существование таких ненулевых непрерывных функций Ψ1(t),Ψ2 (t),...,Ψn (t) , что для всех

t [t0 ,t1] функция H переменных u1, u2 ,..., ur в заданной области их допустимых значений достигает максимума, т.е. H (Ψ, x,u) = max H , причём величина max H

постоянна во времени и max H ≥ 0 .

u U

Согласно приведенным формулировкам принцип максимума даёт только необходимые условия оптимальности. Вопрос о достаточности условий сложен, поэтому в практических приложениях заранее интуитивно предполагают достаточность по физическому смыслу исследуемой системы.

Пример 7.6. ОУ описывается системой уравнений x&1 = x2 , x&2 = u . Найти

управляющее воздействие, которое за минимальное время переведёт объект из произвольного начального состояния в равновесное x1 = 0; x2 = 0 , при этом

u ≤1.

Составим функцию H (Ψ, x,u) = Ψ1x2 + Ψ2u и определим максимум H по пе-

ременной u: dHdu = Ψ2 = 0 . Это равенство может выполняться только при нулевой функции Ψ2 (t) , поэтому максимум H достигается на границе области допусти-

140

Управление u , максимизирующее H, определим из равенства

∂∂H = K1 Ψ1(t) = 0. u T1

Равенство (7.59) возможно только при Ψ1(t) = 0 , в соответствии с этим для

максимума H необходимо, чтобы u =Umax при Ψ1(t) > 0 и u = −Umax при

Ψ1(t) < 0 , т.е.

u (t) =Umax SignΨ1(t) .

∂∂Hu может зависеть от нескольких или от суммы всех со-

ставляющих вектора Ψ(t) .

Для определения характера управляющего воздействия нужно знать, сколько раз функция Ψ1(t) меняет знак или, иначе говоря, сколько корней имеет функция

Ψ1(t) . При прохождении функции Ψ1(t) через нуль каждый раз будет происхо-

дить смена знака управляющего воздействия. Моменты смены знака управляющего воздействия называются моментами переключения.

А.А. Фельдбаум в 1953 г. доказал теорему об n-интервалах, которая позволяет определить вид оптимального управления, не анализируя функции Ψ1(t): ес-

ли ОУ описывается линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами и корни его характеристического уравнения вещественные отрицательные или нулевые, то для оптимального управления необходимо и достаточно n-интервалов максимального значения управления Umax , а

знаки на интервалах должны чередоваться (n −1) раз.

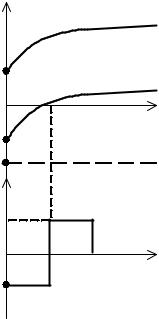
В соответствии с теоремой об n-интервалах оптимальное управление для рассматриваемого ОУ (7.57) имеет вид, показанный на рис. 7.12.

Следует отметить, что теорема об n-интервалах указывает только форму оптимального процесса, но не даёт закона определения продолжительности интервалов постоянства и моментов переключения.

142