Тема 3. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

3.1. Математическая формулировка и основные особенности задачи линейного программирования

В наиболее общем виде задача ЛП формулируется следующим образом.

Найти значения переменных xi ≥ 0, i =1,..., n , доставляющих экстремум линейной функции цели

Здесь cT =[c1,c2 ,...,cn ] – транспонированный n-мерный вектор постоянных

где А – постоянная матрица размерности m×n, В – m-мерный постоянный вектор. В сформулированной задаче имеется q ограничений типа неравенств и m − q

ограничений типа равенств. Если ограничения типа неравенств отсутствуют, то такая форма записи задачи ЛП называется канонической. Общая форма записи ограничений может быть приведена к канонической путем введения дополнительных переменных. Дополнительные неотрицательные переменные вводятся таким образом, чтобы привести ограничения неравенства к виду равенств. В зависимости от знака неравенств (3.2) и (3.3) будут иметь место следующие выражения:

13

где x – N-мерный вектор, включающий в себя как n основных, так и q дополнительных переменных (N = n + q) , A1 – постоянная матрица размерности m × N .

Введение дополнительных переменных не изменяет функции цели и не влияет на оптимальное решение задачи. В дальнейшем ограничимся задачей максимизации функции цели. При этом общность не ограничивается, так как максимизация функции F1(x) эквивалентна минимизации функции

F(x) = −F1(x) .

Теперь задача ЛП может быть сформулирована в следующей канонической форме:

Рассмотрим особенности задач ЛП. Система ограничений (3.6) представляет собой m линейных алгебраических уравнений с N неизвестными переменными. Если N = m и матрица A1 неособенная (т.е. det A1 ≠ 0, то существует единственное решение системы и варьировать переменные для обеспечения минимума F(x) оказывается невозможным. Если N < m , то некоторые уравнения являются

зависимыми и могут быть исключены, при этом возвращаемся к случаю, когда m = N. Это означает, что задача ЛП имеет смысл только при N > m , т.е. когда общее число неизвестных больше числа ограничений. В этом случае из множества решений системы (3.6) необходимо выбрать такое, которое придает целевой функции максимальное значение.

Отметим, что при отсутствии ограничений функция цели (3.7) не имеет экс-

тремума. Поэтому экстремум, если он существует, обязательно будет граничным, а не внутренним.

Так как все ограничения линейны, то множество допустимых решений явля-

ется выпуклым. Следовательно, экстремум целевой функции в задаче ЛП, если он существует, всегда является глобальным.

14

3.2. Графическая интерпретация задачи линейного программирования

Для более полного представления о задаче ЛП сделаем её геометрическую интерпретацию. Совокупность любого числа линейных ограничений выделяет в пространстве x1, x2 ,..., xn некоторый выпуклый многогранник, ограничивающий

область допустимых значений переменных (ОДЗП). Геометрическую интерпре-

тацию и решение задачи нетрудно получить лишь в простейших случаях при n = 2 или n = 3. Рассмотрим задачу:

пересечения m полуплоскостей. Условия неотрицательности позволяют ограничиться рассмотрением положительного квадранта.

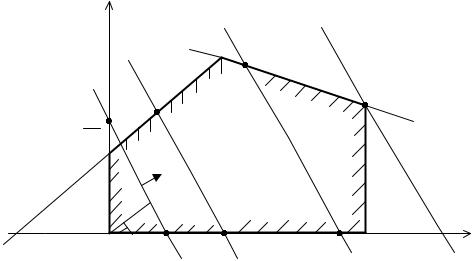
На рис. 3.1 показан один из возможных вариантов ОДЗП в виде замкнутого многоугольника для случая m = 3.

X2

d

α

X1

0 F1/C1

Рис. 3.1. Графическая интерпретация задачи ЛП

Координаты x1 и x2 любой точки, принадлежащей области, удовлетворяют

системе ограничений задачи. Чтобы найти оптимальное решение, зададим функции цели некоторое постоянное значение F1 = c1x1 + c2 x2 = const и построим пря-

15

F2 , F3 ,... и изобразить соответствующие линии, то получим семейство параллель-

ных прямых, которые называются линиями уровня функции цели. Направление стрелки показывает направление увеличения целевой функции F1 < F2 < F3 <... .

Величину функции цели можно характеризовать расстоянием d от начала коор-

динат до линии уровня в соответствии с выражением d = F1 sin α. c1

В теории ЛП доказано, что если оптимальное решение задачи существует и единственно, то оно достигается в некоторой вершине многоугольника решений. Очевидно, что целевая функция достигает максимального значения тогда, когда её линия будет проходить через точку M. Координаты этой точки будут оптимальным решением задачи. Минимальное значение рассматриваемой функции будет достигаться в начале координат. Таким образом, если требуется определить такие x1 и x2 , которые обеспечивают максимум функции цели, то геометрически

это означает, что необходимо провести прямую F = const , проходящую хотя бы через одну вершину области и имеющую максимальное расстояние d от начала координат.

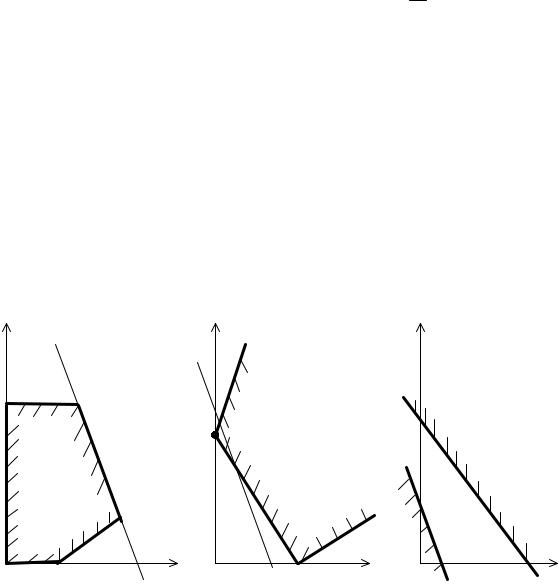
В случае минимизации это расстояние должно быть минимальным. В зависимости от вида ОДЗП и расположения линий уровня могут встретиться случаи, изображенные на рис. 3.2.

F=const

B

А ОДЗП

Рис. 3.2. Различные варианты решения задач ЛП

16