На рис. 4.6 F ' (z) < 0 , поэтому следующий интервал, на котором ищется экстремум функции [z, N ] и «секущая» проводится через точки F ' (z) и F ' (N) , находится очередное приближение z1 к экстремуму и т.д.

4.1.4. Методы полиномиальной аппроксимации. Логическая структура по-

иска с помощью метода исключения интервалов основана на простом сравнении значений функции в двух пробных точках. При этом в расчет принимается только отношение порядка на множестве значений функции и не учитывается величина разности между значениями функции.

Рассмотрим методы поиска, которые позволяют учесть относительные изменения значений функции и являются в ряде случаев более эффективными, чем методы исключения интервалов.

Выигрыш в эффективности достигается ценой введения дополнительного требования, согласно которому исследуемые функции должны быть достаточно гладкими.

Основная идея методов: по информации о m испытаниях (xi , F (xi )), i =1, m строится аппроксимирующий полином ϕ(x) степени n ≤ m −1, который

используется для оценивания координаты точки экстремума.

Качество оценок координаты точки оптимума можно повысить двумя методами:

1)использование полинома более высокого порядка;

2)уменьшение интервала аппроксимации.

Однако построение аппроксимирующего полинома порядка выше третьего становится весьма сложной процедурой, поэтому второму способу отдается предпочтение.

Метод квадратичной аппроксимации. Для трех точек испытаний ( m = 3 )

Величины α0 , α1 и α2 должны быть такими, чтобы значения ϕ(x) и F(x)

60

Таким образом, по результатам трех испытаний можно найти коэффициенты α0 , α1 , α2 аппроксимирующего квадратичного полинома. Для нахождения экс-

тремума приравнивается к нулю первая производная полинома ϕ(x) :

ddxϕ = α1 + 2α2 x − α2 (x1 + x2 ) = 0 ,

тогда оценочное значение xˆ координаты точки экстремума вычисляется следующим образом:

Как правило, точки x* и xˆ точно не совпадают. При поиске минимума унимодальной функции с высокой степенью точности ε необходимо последовательно применять сначала методы сокращения интервала неопределенности, а затем методы полиномиальной аппроксимации.

Пусть задана совокупность удачных точек a, x0 , b . На рис. 4.7 приведена

блок-схема алгоритма, реализующего поиск минимума унимодальной функции F(x) с использованием квадратичной аппроксимации и метода сокращения ин-

тервала неопределенности.

Метод кубической аппроксимации. Для четырех точек испытаний поиск минимума можно вести с помощью метода кубической аппроксимации. В качестве аппроксимирующего полинома ϕ(x) используется кубическая парабола

61

Не нарушая общности, можно предположить, что рассматриваются точки на

то xˆ = ak + (bk − ak )xˆ1 .

Дальнейшая процедура поиска минимума аналогична процедуре предыдущего метода и связана с сокращением интервала неопределенности.

Построение аппроксимирующего полинома можно выполнить и на основе меньшего числа точек, если в каждой точке вычислять не только значения функции, но и ее производные.

Аппроксимирующая кубическая функция записывается в виде

ϕ(x) = α0 + α1 (x − x1 ) + α2 (x − x1 )(x − x2 ) + α3 (x − x1 )2 (x − x2 ) . (4.18)

Коэффициенты αi подбираются так, чтобы значение ϕ(x) и ее производных в точках x1 и x2 совпадали со значениями F(x) и F ' (x) в этих точках:

63

ϕ' (x1) = F ' (x1) = α1 + α2 (x1 − x2 ) ;

ϕ' (x2 ) = F ' (x2 ) = α1 + α2 (x2 − x1 ) + α3 (x2 − x1 )2 .

После того как коэффициенты найдены, можно оценить координаты точки экстремума, приравнивая нулю производную.

Далее необходимо действовать по аналогии со случаем квадратичной функ-

ции.

4.2. Поиск безусловного экстремума функций многих переменных

Задача формулируется следующим образом: найти значения переменных x1, x2,…, xn , доставляющие экстремум скалярной целевой функции F(x1, x2,…, xn), если ограничения на переменные отсутствуют. Удобно предположить, что функция F и ее производные существуют и непрерывны.

Рассмотрим некоторые фундаментальные понятия, используемые при поиске экстремума.

Градиент функции F(x) – это вектор, составляющие которого равны частным производным функции F(x) по соответствующим переменным, т.е.

− F(x) называется антиградиентом, его направление совпадает с направлением наискорейшего убывания функции.

Матрица вторых производных 2 F(x) – это симметричная квадратная матрица порядка n вторых частных производных функции F(x). Эту матрицу называют матрицей Гессе и обозначают H (x) = 2 F(x) . Ее элемент, расположенный

на пересечении i-й строки и j-го столбца, равен ∂2 F .

∂xi∂x j

64

Необходимые и достаточные условия существования экстремума. Пусть

хТ=[x1 , x2,…, xn] – вектор переменных. Для наличия в точке x* локального минимума (максимума) необходимо, чтобы выполнялось равенство F(x*) = 0 и мат-

рица Гессе H (x*) = 2 F(x*) была положительно (отрицательно) полуопределен-

ной, т.е. xT Hx ≥ 0 ( xT Hx ≤ 0 ).

Достаточным условием существования минимума (максимума) в точке x* является положительная (отрицательная) определённость матрицы Гессе в этой точ-

ке, т.е. xT Hx > 0 ( xT Hx < 0 ).

Методы решения задач безусловной оптимизации можно разделить на три класса:

1.Методы прямого поиска, основанные только на вычислении значений целевой функции.

2.Градиентные методы, в которых используются значения первых производных F(x).

3.Методы второго порядка, в которых наряду с первыми производными используются также вторые производные функции F(x).

В ряде практических инженерных задач присутствует информация только о значениях целевой функции, поэтому прямые методы имеют важное значение, хотя требуют большего количества вычислений значений функции.

4.2.1. Метод Нелдера-Мида. Метод является одним из методов прямого поиска по симплексу. Суть его в следующем.

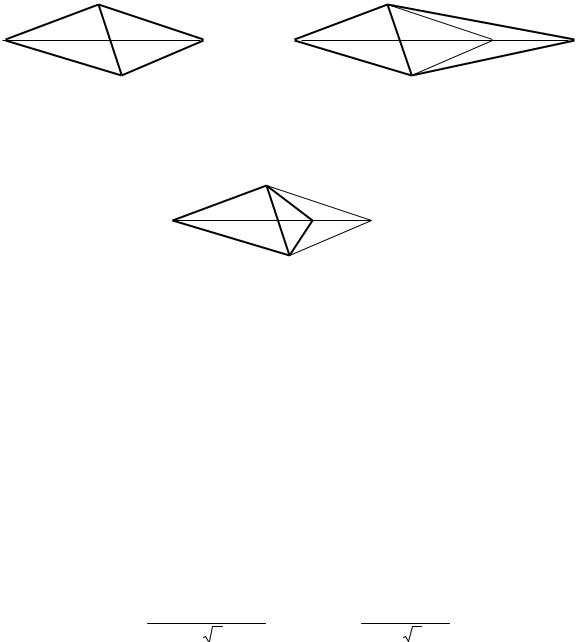
В области допустимых значений переменных выбирается начальная точка и оценивается значение целевой функции в определённых точках, окружающих базовую. «Наилучшая» из исследуемых точек принимается начальной на следующем шаге. В качестве точек эксперимента выбираются вершины симплекса. Симплекс в N-мерном пространстве представляет собой многогранник, образованный N+1 равноотстоящими друг от друга точками-вершинами. В случае двух переменных симплексом является равносторонний треугольник, в трёхмерном пространстве треугольная пирамида и т.д.

На рис. 4.9, а в виде равностороннего треугольника с вершинами x0, x1 и x2 приведен симплекс для функции двух переменных. В каждой из вершин симплекса оценивается значение целевой функции и при поиске минимума определяется вершина, которой соответствует наибольшее значение функции. Пусть это будет вершина x1. Далее находится середина отрезка x0 x2 (центр тяжести) xC, и точка x1 проецируется через неё в новую точку x3, которая используется в качестве вершины при построении нового симплекса ( x0 x2 x3 ).

Поиск завершается, когда разности между значениями функции в вершинах становятся достаточно малыми или диаметр симплекса становится меньше заданной величины итерационной погрешности по переменным x.

65