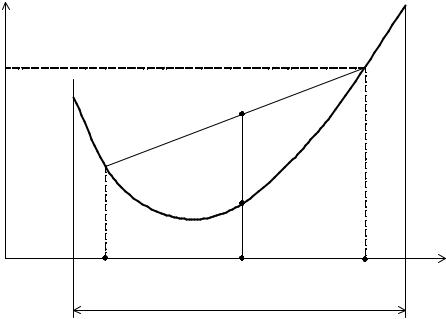
щей две точки на её поверхности. Если знак неравенства (2.2) изменить на обрат-
ный, то F(x) будет вогнутой, или выпуклой вверх функцией.
F(x)
F(x2)
|
|
|
|
|
|
|
|
x) |
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
F |
2 |
|
|
|
|
|
|
|
) |
|
||
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
x) |
|
|
|
|
|
|
|
|
( 1 |
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
F(x1) 
F[αx1+(1-α) x2]
x1 |
αx1+(1-α)x2 |
x2 |
x |
|
Множество S |
|
|
Рис. 2.3. Выпуклая функция одной переменной
Из определения следует, что если F(x) – выпуклая (или строго выпуклая), то − F(x) – вогнутая (или строго вогнутая) функция, или наоборот. Для выпуклой
функции d 2F(x) |
≥ 0 , а для вогнутой — d 2F(x) |
≤ 0. |
dx2 |
dx2 |
|
В отличие от невыпуклых функций, которые могут иметь любое число локальных минимумов, выпуклая функция имеет только глобальный минимум. Задача нахождения минимального значения выпуклой функции F(x) в случае, ко-
гда область допустимых значений переменных определяется системой выпуклых неравенств g j (x) ≤ 0, j =1,m , называется задачей выпуклого программирования.
Любой локальный минимум задачи выпуклого программирования является глобальным минимумом. Это свойство задач выпуклого программирования значительно облегчает поиск их решения.
2.3.Типы задач математического программирования
Взависимости от вида функций цели и типа ограничений задачи МП подразделяются на ряд более частных задач:
10
−линейное программирование: функция цели и ограничения являются линейными функциями переменных xi , i =1, n ;
−нелинейное программирование: функция цели и (или) ограничения являются нелинейными;
−квадратичное программирование: функция цели квадратичная, а ограни-
чения являются линейными функциями переменных xi ,i =1, n ;
−сепарабельное программирование: функция цели и ограничения являются сепарабельными функциями, т.е. представлены в виде сумм n функций, каждая из которых зависит только от одной переменной;
−геометрическое программирование: функция цели и ограничения пред-
m |
n |
αij , где |
ставлены с помощью положительных полиномов вида ∑ci ∏x j |
||
i =1 |
j =1 |
|
ci – постоянные положительные коэффициенты, i =1, m ; αij – произвольные действительные числа, j =1, n;
− целочисленное программирование – это задачи, в которых переменные xi
могут принимать только целые значения;
− стохастическое программирование: коэффициенты в целевой функции или в ограничениях являются случайными величинами.
2.4.Связь между задачей математического программирования
изадачей оптимального управления
Как уже отмечалось, задача оптимального управления заключается в отыскании такого алгоритма управления u* (t) U , который переводит ОУ из заданного начального состояния x0 в конечное xT и обеспечивает экстремум выбранному
критерию качества при соблюдении заданных ограничений. Рассмотрим задачу, в которой критерий оптимальности задан функционалом
T |
|
J = ∫ F [ x(t), u (t), t] dt + G[ x(T ), T ] , |
(2.3) |
t0 |
|
представляющему собой сумму интегральной и терминальной составляющей. Здесь G [x(T ),T ] – терминальная функция, она не зависит от управляющего
воздействия, а определяется только состоянием объекта в конечный момент времени. При этом должны удовлетворяться уравнения состояния системы
11
xi (t) = fi [x(t),u(t),t], i = |
1,n |
|
(2.4) |
& |
|
|
|
и ограничения |
|
||
g[x(t), t] ≤ 0, g[u(t), t] ≤ 0 . |
(2.5) |
||
Задача оптимального управления фактически является задачей МП [8]. Чтобы пояснить это, надо представить интеграл (2.3) в виде суммы, разбив интервал [t0 ,T ] на N временных подинтервалов:
T |
N |
|
|
|
∫F[x(t), u(t), t] dt = lim ∑F[x(tk ), u(tk ),tk ] (tk |
− tk −1) . |
(2.6) |
||
t0 |
N →∞ k =1 |
|
|
|
Уравнения состояния (2.4) при таком разбиении можно представить следую- |
||||
щим образом: |
|
|
|
|
lim |
x(tk ) − x(tk −1) |
= f [x(tk ),u(tk ), tk ], |
|
(2.7) |
|
|
|||
(tk −tk −1 )→0 |
tk − tk −1 |
|
|
|
а ограничения (2.5) – в виде |
|
|
|
|
g[x(tk ), tk ] ≤ 0, g[u(tk ), tk ] ≤ 0 . |
|
(2.8) |
||
Другими словами, интегрирование заменяется конечным суммированием, а дифференциальные уравнения – разностными уравнениями. Объединим (2.6) –
(2.8), вводя обозначения tk − tk −1 |
= ∆, x(tk ) − x(tk −1 ) = ∆x . При этом получим за- |
|||||
дачу МП: |
|
|
|
|
|
|
min(max) lim |
N |
|
|
∆x |
|
|
|
|
|
|
|||
∑ F [ x (tk ), u (tk ), tk ] ∆ +G [ x (t N )] |
lim |
= |
|
|||
|
|
|||||
N → ∞ k =1 |
|
∆ → 0 |
∆ |
|
||
|
|
|
||||
= f [ x (t k ), |
u (t k ), t k ], |
g [ x (t k ), t k ] ≤ 0 , g [u (t k ), t k ] |
≤ 0 }, |
(2.9) |
||
в которой неизвестными являются x(tk ) , u(tk ) .
Число переменных в (2.9) бесконечно, т.е. задача оптимального управления для непрерывной системы образует бесконечномерную задачу МП. При решении практических задач число переменных может быть уменьшено до приемлемой величины. Большая часть работ, посвященных решению задач оптимального управления методами МП, относится к линейным системам. При этом задача оптимального управления сводится к решению задачи линейного программирования
(ЛП).
12