Следует заметить, что от итерации к итерации значение функции цели уменьшается. Истинный экстремум x* =[1,5; 1,5] может быть достигнут на сле-

дующем шаге. С графической точки зрения x* – это точка касания одной из линий уровня со стороной ВС ОДЗП.

6.2. Метод отсекающих плоскостей Кэлли

Метод ориентирован на решение задач оптимизации с линейной функцией цели F(x) и нелинейными ограничениями, и позволяет свести исходную нели-

нейную задачу к последовательности линейных подзадач, полученных в результате линеаризации ограничений.

Рассмотрим следующую задачу МП:

где g j (x) – выпуклые функции.

Предполагается, что область допустимых значений переменных X ограничена и непуста. Простейшим линейным приближением к X служит содержащий

Это достаточно грубая, но наиболее простая аппроксимация.

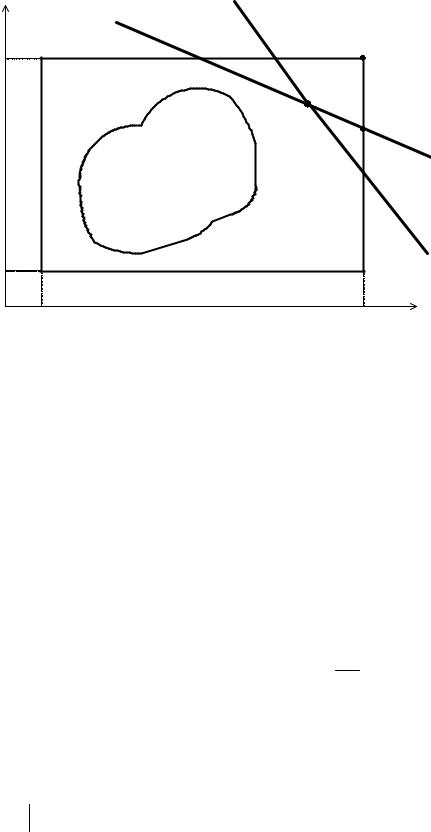
На рис. 6.2 показана замена нелинейной области X для случая двух переменных прямоугольником, определяющим линейную область

Z 0 ={x a1 ≤ x1 ≤ b1;a2 ≤ x2 ≤ b2}.

Используя это приближение в качестве ограничения, получим следующую первую подзадачу ЛП:

Пусть оптимальное решение задачи (6.5) x1* . С графической точки зрения – это одна из вершин области Z 0 (рис. 6.2). Наиболее вероятно, что истинный оп-

тимум задачи (6.4) расположен в наиболее близкой к x1* части X , поэтому именно эту часть исследуют для получения улучшенной аппроксимации.

100

a2

Рис. 6.2. Линейная аппроксимация допустимой области

В окрестности точки x1* строятся отсекающие плоскости при помощи локальной линеаризации нарушаемых ограничений. Линеаризация любого, нару-

шающегося в точке x1* ограничения g j (x) ≥ 0, осуществляется в соответствии с выражением

Келли предложил осуществлять на каждой итерации линеаризацию только одного ограничения g p (x) , которое нарушается в рассматриваемой точке наибо-

лее сильно. Если в условии задачи g j (x) ≥ 0 , то наиболее нарушаемое ограничение g p (x) определится из условия

− g p (x1* ) = max[−g j (x1* ),0], j =1,m .

сте с точкой x1* , но не затрагивает X. В результате получается некоторая меньшая

область Z 1 , представляющая собой ОДЗП для второй линейной подзадачи max{F(x) = cT x x Z1}.

101

Оптимальное решение x2* этой подзадачи с графической точки зрения соот-

ветствует одной из вершин области Z1 (рис. 6.2). Далее проверяется, какое из нелинейных ограничений нарушается в этой точке наиболее сильно, и оно подверга-

Алгоритм решения задачи (6.4) методом отсекающих плоскостей Кэлли: 1-й шаг. Задать начальные границы линейной ОДЗП

Z 0 ={x ai ≤ xi ≤ bi ,i =1, n},

так, чтобы X Z 0 , и определить точность ε > 0 решения задачи. 2-й шаг. Решить задачу ЛП:

max{F(x) = cT x x Z 0}.

Пусть x1* – оптимальное решение задачи. Для k = 1,2,… выполнить следующую последовательность шагов.

3-й шаг. Найти такое р, что

− g p (xk*) = max[−g j (xk*),0], j =1, m ,

т.е. выбрать то ограничение, которое нарушается наиболее сильно.

Если g p (xk* ) > −ε, то прекратить вычисления. В противном случае перейти

к 4-му шагу.

4-й шаг. Построить отсекающую плоскость, определяющую дополнительное ограничение, используя выражение

Определить новую область допустимых значений Z k . 5-й шаг. Решить задачу ЛП

max{F(x) = cT x x Z k }.

Обозначим через x(k +1)* оптимальное решение этой задачи. 6-й шаг. Положить k = k+1 и перейти к 3-му шагу.

102

Важным преимуществом метода Кэлли (общим для всех методов линеаризации) является сохранение любой линейности в исходной задаче. Кроме того, решаемая на каждой итерации подзадача является задачей ЛП, для решения которых разработаны наиболее эффективные методы.

Пример 6.2. Решить задачу методом отсекающих плоскостей Кэли:

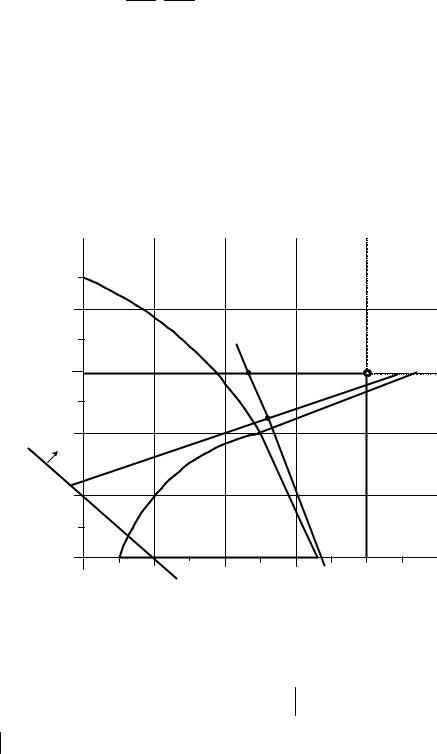
штрихованная область на рис. 6.3). Значения переменных для построения графи- ков g1(x) и g2 (x)

Т а б л и ц а 6.7

Первая итерация.

1-й шаг. Начальные границы линейной области Z 0 зададим условиями 0 ≤ x1 ≤ 4 и 0 ≤ x2 ≤ 3 , которые определяют соответствующий прямоугольник,

включающий X (рис. 6.3).

2-й шаг. Находим максимальное значение функции F(x) = x1 + x2 при ли-

нейных ограничениях, определяющих область Z 0 . Очевидно, что решением является точка x1* =[4, 3], при этом F(x1* ) = 7 .

3-й шаг. Вычисляются значения ограничений в точке x1* : g1(x1*) = −2, g2 (x1* ) = −9,8 . Наиболее сильно нарушается ограничение g2 (x) ≥ 0 .

4-й шаг. Осуществляется линеаризация ограничения g2 (x) в точке x1* в со-

103

5-й шаг. Решается задача ЛП с новыми ограничениями: max{F(x) = x1 + x2 x Z1},

где Z1 ={x 3,2x1 + x2 ≤10,9; 0 ≤ x2 ≤ 3; x1 ≥ 0}.

Решение можно осуществлять графически (одна из линий уровня функции цели для F =1 показана на рис. 6.3), либо с помощью симплекс-метода

(табл. 6.8 – 6.10).

104