5)при options(5) = 1 – метод Gauss-Neuton;

6)по умолчанию (options(5) = 0) – метод Levenberg-Marquardt.

Функция LEASTSQ преобразует целевую функцию F(x) в квадратичную F2(x). Если F(x) является знакопеременной, то минимальные значения функций F(x) и F2(x) не совпадают. Поэтому функция F(x) дополняется константой F(x)+const для устранения знакопеременности. Иначе функция LEASTSQ найдет не минимум F(x), а ее нулевое значение. На каждой итерации осуществляется поиск минимума исследуемой функции по величине шага λ в выбранном направлении (одномерная минимизация).

Для одномерного поиска используются методы полиномиальной аппроксимации, задаваемые значением options(7):

7)по умолчанию (options(7) = 0) – метод смешанной полиномиальной ап-

проксимации Mixed Polynomical Interpolation;

8)при options(7) = 1 – кубическая аппроксимация Cubic Interpolation.

Режим вывода результатов устанавливается одним из значений options(1):

–по умолчанию (options(1) = 0) – вывод промежуточных значений не проис-

ходит;

–при options(1) = 1 – обычный вывод промежуточных значений;

–при options(1) = 2 – расширенный вывод промежуточных значений.

Для контроля вектора градиента options(9) установить в 1. При выводе результатов:

options(8) – значение целевой функции; options(10) – количество выполненных итераций.

Итерационная погрешность задается значением options(2) для аргумента и options(3) для функции, значение погрешности по умолчанию 10-4.

Тема 5. ЭКСТРЕМАЛЬНЫЕ НЕЛИНЕЙНЫЕ ЗАДАЧИ

СОГРАНИЧЕНИЯМИ

Внелинейном программировании (НП) рассматриваются задачи отыскания экстремума функции многих переменных при наличии ограничений на переменные в виде неравенств, при этом функция цели или хотя бы одно ограничение нелинейны. Задача НП формулируется следующим образом.

Найти значения переменных x1, x2 ,..., xn минимизирующие скалярную целевую

функцию F(x1, x2 ,..., xn ) при наличии ограничений вида g j (x) ≤ 0, j =1, m , где по крайней мере одна из функций F(x) и g(x) является нелинейной.

Методы решения задач НП по сравнению с задачами ЛП обладают большим многообразием. Экстремум в задачах НП может достигаться не только в вершине

80

или на границе области допустимых значений переменных, но и внутри области. Допускаются любые соотношения между количеством переменных n и числом m ограничений задачи, т.е. n<m, n=m, n>m. Решение задач НП может давать два или несколько экстремумов, что требует дополнительных проверок результата решения.

5.1. Метод неопределенных множителей Лагранжа

Метод отыскания условного экстремума функции многих переменных в задачах с ограничениями равенствами при отсутствии требований неотрицательности и целочисленности переменных был предложен Лагранжем и называется ме-

тодом множителей Лагранжа.

Преобразуем их к виду bj − ϕj (x) = g j (x) = 0 . Будем полагать, что функции F(x) и g(x) непрерывны и имеют непрерывные частные производные. Образуем вспомогательную функцию L(x,λ), объединив функцию F(x) с ограничениями, используя неотрицательные постоянные множители λ1,..., λm

m

L(x, λ) = F(x) + ∑λ j g j (x) = F(x) + λТg(x) . (5.2)

j =1

Справедлива следующая теорема: если функция F(x) достигает своего экстремума при условиях (5.1) в точке x1*, x2* ,..., xn* , то существуют такие числа λ1, λ2 ,..., λm , что для функции L(x,λ) в точке x1*,..., xn* выполняются необходимые условия безусловного экстремума, т.е.

Функция L(x,λ) называется функцией Лагранжа, a числа λ1,..., λm – неоп-

ределенными множителями Лагранжа.

Таким образом, вычисление условного экстремума функции F(x) сводится к

отысканию безусловного экстремума функции Лагранжа (5.2). Задача состоит в нахождении n + m неизвестных, включающих n переменных х и m множителей

81

Лагранжа. Для их определения используется система из m ограничений и n уравнений (5.3) являющихся условиями экстремума функции Лагранжа.

Множители Лагранжа имеют определенный смысл. Предположим, что правые части системы ограничений (5.1) могут в некоторых пределах изменяться. Если рассматривать функцию Лагранжа как функцию вектора b, т.е.

m

L(x, λ,b) = F(x) + ∑λ j [bj − ϕj (x)],

j =1

то выполняется соотношение

∂∂L = λ j , j =1,m . b j

Но для оптимального решения L(x*, λ) ≡ F(x*), поэтому множители Лагранжа показывают, как реагирует целевая функция на изменение соответствующих

параметров bj , т.е. ∆F ≈ λ j .

∆bj

Если F интерпретировать как прибыль или стоимость, а bj как некоторые ресурсы, то λ j будут показывать как изменится максимальная прибыль (или минимальная стоимость) при увеличении количества j-го ресурса на единицу.

5.2. Теорема Куна-Таккера

Одной из важнейших теорем в теории НП является теорема Куна-Таккера, обобщающая классический метод неопределенных множителей Лагранжа на за-

дачи с ограничениями неравенствами вида g j (x) ≤ 0, j =1,m и ограничениями на

знак переменных xi ≥ 0, i =1, n. Пусть имеется следующая задача:

min{F(x1, x2 ,...xn ) g j (x1, x2 ,...xn ) ≤ 0, j =1, m,xi ≥ 0,i =1, n}, (5.4)

где F(x) и gj(x) – выпуклые функции n переменных.

m

Введем функцию Лагранжа L(x,λ) = F(x) + ∑λ j g j (x) , используя совокуп-

j =1

ность неопределенных множителей Лагранжа λ1, λ2 ,..., λm.

Теорема Куна-Таккера формулируется следующим образом. Пусть сущест-

82

вует вектор x, такой, что xi ≥ 0,i =1,n и g j (x) ≤ 0, j =1, m. Тогда для того, чтобы

вектор x* был оптимальным решением задачи (5.4), необходимо и достаточно, чтобы существовал неотрицательный m-мерный вектор λ, такой что

для всех x ≥ 0, λ ≥ 0.

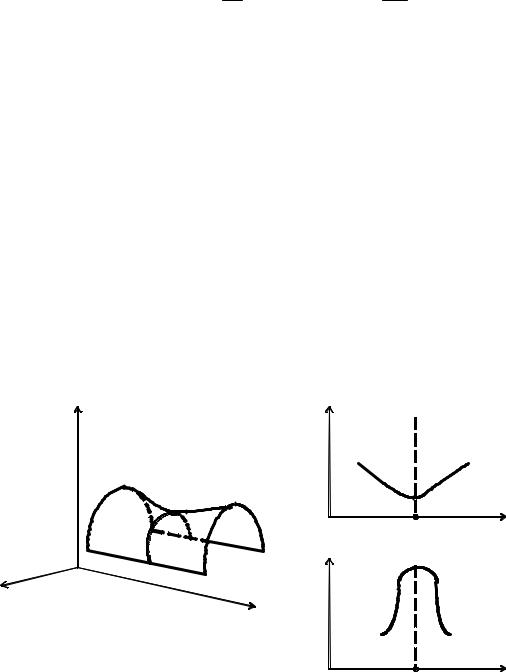
Выражение (5.5) означает, что функция L в точке ( x*, λ* ) при фиксированном x* имеет глобальный максимум в области λ ≥ 0 при λ = λ* , а при фиксированном λ* она имеет глобальный минимум в области x ≥ 0 при x = x*. Экстремальная точка ( x*, λ* ) с такими свойствами называется cедловой точкой, а теорему Куна-

Таккера часто называют теоремой о седловой точке. Итак, задаче (5.4) минимизации F(x) соответствует задача нахождения седловой точки (минимаксная задача) для функции L, в которой из всех ограничений сохраняются только ограничения на знак.

Геометрически соотношение (5.4) интерпретируется с помощью рис. 5.1.

L L

Рис. 5.1. Геометрическая интерпретация теоремы о седловой точке

Если F(x) и g j (x) являются дифференцируемыми функциями, то условия теоремы Куна-Таккера записываются следующим образом:

83