Решение, соответствующее табл. 3.18, является оптимальным. Запишем соответствие между переменными прямой и двойственной задач. Если ограничения прямой задачи приводить к виду равенств, то в качестве дополнительных появятся переменные x3, x4 , x5, x6 .

Тогда

y1, y2 , y5, y4 . С учетом (3.28) найдем оптимальное решение прямой задачи: x3 =8; x4 =8; x1 =1; x6 =1.

Переменная x5 , соответствующая y3, и x2 , соответствующая y6 , равны ну-

лю.

min F( y) = max F(x) = 6 .

Таким образом, решая симплексным методом одну из пары двойственных задач, автоматически получаем решение другой.

3.9. Целочисленное линейное программирование

Специфика задач целочисленного программирования (ЦП) заключается в том, что на переменные xi и функцию цели F(x) налагается дополнительное огра-

ничение – условие целочисленности. ЦП иногда называют дискретным про-

37

граммированием. Если требование целочисленности распространяется не на все переменные, а только на часть из них, то задача называется частично целочис-

ленной.

В большинстве случаев целочисленные задачи сильно отличаются от своих непрерывных аналогов и требуют для решения специальных методов. Условно методы решения задач целочисленного программирования можно разделить на три основных группы: методы отсечения; комбинаторные методы; приближенные методы.

Процедура решения задачи методом отсечения осуществляется следующим образом:

1.Решается задача линейного программирования с отброшенным условием целочисленности. Если в полученном оптимальном решении хотя бы одна переменная или функция цели являются дробными, то переходят ко второму шагу.

2.Строятся дополнительные линейные ограничения, отсекающие от ОДЗП ту её часть, в которой содержится оптимальное решение и не содержится ни одного целочисленного решения.

3.В исходную задачу включается дополнительное ограничение и применяется симплекс-процедура. Если же найденное оптимальное решение опять будет дробным, то формируется новое дополнительное ограничение и процесс вычислений повторяется.

Способы построения дополнительных линейных ограничений известны как алгоритмы Гомори. Они различны для полностью и частично целочисленных задач и обеспечивают решение задачи за конечное число шагов.

3.9.1.Алгоритм Гомори для полностью целочисленной задачи ЛП. Пусть дана следующая задача:

в результате решения которой с отброшенными условиями целочисленности получена оптимальная симплекс-таблица (табл. 3.19) и оптимальное нецелочисленное решение.

Здесь для удобства через v j ( j =1,m) обозначены базисные переменные в

оптимальном решении задачи, а через wi (i =1, n) – небазисные переменные. Для любой j-й строки симплекс-таблицы справедливо равенство:

n

∑α ji wi + v j = βj . (3.30)

i =1

38

где выражение в [ ] означает наибольшее целое число, не превышающее исходное, а выражение в {} – дробную положительную часть числа, например

Подставим (3.31) в (3.30)

и преобразуем (3.32) следующим образом

n

v j − [βj ] + ∑[α ji ] wi = {βj } −{α ji } wi . (3.33) i =1

Так как переменные v j и wi должны быть целыми, левая часть (3.33) также

целая, следовательно, правая часть уравнения (3.33) может принимать только целые значения. Для того, чтобы правая часть была целой, необходимо выполнение неравенства:

Выражение (3.34) представляет дополнительное линейное ограничение, или отсечение Гомори, которое определяет гиперплоскость, отсекающую нецелочисленные решения задачи вместе с частью ОДЗП и сохраняющую при этом все це-

39

лые решения. Дополнительное ограничение составляется по той строке, переменной v j которой соответствует наибольшая дробная часть. Признаком отсутствия

целочисленного решения служит наличие в таблице хотя бы одной строки с дробным свободным членом и целыми остальными коэффициентами. Задача (3.29) с добавлением ограничения (3.34) называется расширенной. Соответствующее ей решение не является допустимым, поэтому вначале находим допустимое базисное решение, а затем переходим к процедуре оптимизации.

Пример 3.8. Найти оптимальное целочисленное решение:

F(x) = x1+5x2 (max);

x1 + x2 ≤ 7;

− 2x1 + x2 ≤ 2;x1 ≤ 4;

x1,2 ≥ 0 ицелые.

Процедура решения задачи с отброшенными целочисленными условиями иллюстрируется симплекс-таблицами 3.20 – 3.22.

40

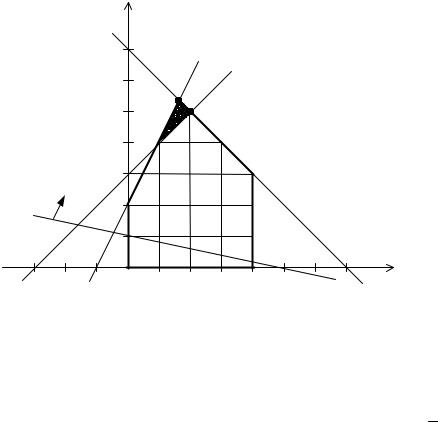
Графическая интерпретация решения представлена на рис. 3.6.

x2

Рис. 3.6. Графическая интерпретация примера 3.8

Дополнительное ограничение составляем по строке, соответствующей пере-

менной x1 в табл. 3.22, так как у нее наибольшая дробная часть: {x1}= 23 .

На основании (3.34) получаем:

Приведем (3.35) к виду равенства, вводя дополнительную переменную x6 и одновременно умножая на (-1). Тогда

С учетом (3.36) симплекс-таблица расширенной задачи представлена табл. 3.23. Осуществляя оптимизацию, найдем, что оптимальное целочисленное

решение определяется по табл. 3.24: x1* = 2; x2* = 5; Fmax = 27.

При нахождении оптимального целочисленного решения всегда происходит проигрыш в величине экстремального значения функции-цели.

41