5.6.4. Метод градієнту

У даному засобі використовується градієнт цільової функції.

На відміну від засобу релаксації в даному засобі кроки учиняються на напрямку найбистрішого зменшення цільової функції, а не по осьовим напрямкам. Такий підхід, природно, прискорює процес пошуку оптимуму.

Процес пошуку оптимуму у засобі градієнту також здійснюється в два етапу. На першому знаходяться значення приватних похідних по всім незалежним перемінним, що і визначає напрямок градієнту в точці ,що розглядається. На другому етапі здійснюється крок в напрямку, зворотному напрямку градієнту, тобто у напрямку найскорішого спадання цільової функції.

При виконанні кроку одночасно змінюються значення всіх незалежних перемінних. Кожна з них отримує припущення, пропорційне відповідної що складає градієнт по наданій осі. По суті в засобі градієнту застосовує ота ж інформація про цільову функцію, що і в засобі релаксації при виборі осьового напрямку, але спуск виробляється по оптимальному шляху.

Алгоритм градiєнтного пошуку може бути записаний наступним образом :

(5.43)

В алгоритмі (5. 43) для градiєнтного пошуку застосовується нормалізований вектор градієнту, зазначаючий лише напрямок найскорішого зміну цільової функції, але він не зазначає швидкості зміни по цьому напрямку. При цьому крок пошуку визначається величиною h^к, стратегію зміни якої можна будувати незалежно від абсолютної величини градієнту.

Можна використовувати інший алгоритм градiєнтного засобу у виді:

U^k+1_j=U^k_j - h⁰ dR(U^k)/dU_j (5.44)

В цьому випадку величина кроку ΔU^K_j= -h⁰ dR(U^K)/dU_j при постійному значенні параметраh змінюється автоматично відповідно до зміною абсолютної величини градієнту. Алгоритм (5.44) володіє отим достоїнством , що при наближенні до оптимуму величина кроку ΔU^к_jавтоматично зменшується. Взагалі, задача вибору стратегії зміни величини кроку у градієнтнім пошуку більш важна, чим в засобі релаксації, тому що після кожного кроку тут необхідно знаходити похідні цільової функції, розрахунок яких пов'язаний з обчисленням n значень цільової функції. Дрібний крок вимагає великого обсягу вичислений, при великому кроці - можливо " рисканiє " в районі оптимуму.

Момент закінчення пошуку визначається по заздалегідь заданим умовам. Один з можливих варіантів - виконання нерівняння (5. 40). Інший варіант після кожної серії з заданим числом кроків S запам’ятається значення цільової функції. Число кроків S у серії вибирається таким, щоб на початкових етапах пошуку діялося помітна зміна значення цільової функції (R). Якщо наступна серія кроків дає менше значення R, отже пошук продовжується. Якщо ж при виконанні слідкуючої серії менше значення R не знаходиться, отже пошук припиняється таі одержане найменше значення роздивляється як iскомий оптимум.

Браком градiєнтного засобу є отже, що при його використанні можна виявити тільки локальний мінімум. Для отого, щоб знайти у функції інші локальні мінімуми, необхідно проводити пошук з інших початкових точок.

Таким чином, за допомогою засобу градієнту кожний локальний мінімум цільової функції можна охарактеризувати деякою областю "притяжіння", що володіє отієї властивістю, що при завданні початкового стану U в кордонах цієї області засіб градієнту завжди приводить в один і отой же локальний мінімум.

Розглянемо один з простіших алгоритмів реалізації засобу градієнту.

Вибираємо координати початкової точки U_1nU_2n, величину кроку H₁та H₂, припущення e₁та e₂.

Визначимо градієнт цільової функції

(5.45)

Для розрахунку ΔR необхідно обчислити величини похідних dR/dU_i.

Визначимо їх численними засобами . Біля початкової крапки1 з координатами (U_1n ,U_2n ) ставляться дві допоміжні крапки: 1’- на відстані ε₁ уздовж осі U₁ і 1''- на відстані ε₂ уздовж осі U₂ (рис. 5.21) У цих крапках розраховуються значення цільової функції R(Х₁, Х₂). Похідні знаходяться по наступним формулах:

(5. 46)

(5. 47)

Рис 5.21

Після цього роблять крок в точку 2 для наступного розрахунку R(Х₁ Х₂). Координати цієї точки визначаються по формулі:

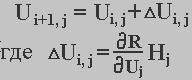
(5.48)

Подальший алгоритм розрахунків будують по-різному. В простому варіанті можна просто повторювати описану вище процедуру. О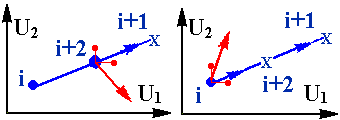днак, частіше роблять інакше. Якщо крок опинився вдалим, отже роблять ще крок в тому ж напрямку, використовуючи знайдені значення похідних на попереднім кроці. Практично це вже не буде напрямком градієнту, але якщо наступний крок дає потрібне припущення R (Х₁Х₂), отже це дозволить "зекономити" на розрахунку похідних. Якщо і цей крок удалий, отже можна зробити крок ще раз і так далі.

Якщо ж крок невдалий - в цьому випадку крок зменшують вдвічі та розраховують точку i+2. Тепер, якщо зменшений крок був удалий, отже рухатися по отому ж напрямку немає змісту , тому що прийдемо в "погану " точку i+1.

В цьому випадку біля точки i+2 ставляться допоміжні точки, розраховуються похідні та визначається нове направлення градієнту. Якщо ж і зменшений крок не приведе в "гарну" точку, отже повертаємося в точку i та будемо шукати новий напрямок градієнту в неї