
- •Министерство образования и науки, молодёжи и спорта украины
- •Одесский национальный политехнический университет
- •Институт компьютерных систем
- •Кафедра информационных систем
- •Министерство образования и науки, молодёжи и спорта украины
- •Одесский национальный политехнический университет
- •Институт компьютерных систем
- •Кафедра информационных систем
- •Содержание
- •Тема1. Формы представления информации 10
- •Тема 2. Логические основы построения элементов 16
- •Тема 3. Схемотехника комбинационных узлов 29
- •Тема 4. Схемотехника цифровых элементов 70
- •Тема 5. Схемотехника цифровых узлов 108
- •Тема 6. Интегрированные системы элементов 138
- •Тема 7. Схемотехника аналоговых узлов 179
- •Тема 8. Схемотехника обслуживающих элементов 208
- •Тема 14. Структуры микропроцессорных систем 293
- •Тема 15. Схемы поддержки мп на системных платах 340
- •Тема 16. Некоторые вопросы развития архитектуры эвм 357
- •Тема 17. Risk – процессоры 387
- •Тема 18. Суперкомпьютеры. Параллельные вычислительные системы 399
- •Список литературы 450 Тема1. Формы представления информации Лекция 1. Основные понятия
- •Тема 2. Логические основы построения элементов Лекция 2.
- •2.1. Основные понятия, определения и законы Булевой алгебры
- •Формы задания Булевой функции
- •2.2. Простейшие модели логических элементов и система их параметров
- •2.3. Типы выходных каскадов цифровых элементов
- •2.4. Системы (серии) логических элементов и их основные характеристики
- •2.5 Контрольные вопросы
- •Тема 3. Схемотехника комбинационных узлов Лекция 3
- •3.1 Общие сведения
- •3.2. Шифраторы, дешифраторы и преобразователи кодов: назначения, виды, функционирование, принципы построения
- •3.3. Синтез кс на основе дешифраторов
- •3.4. Мультиплексоры и демультиплексоры
- •3.5. Шинные формирователи
- •3.6 Синтез кс на основе мультиплексоров
- •3.7. Компараторы
- •3.8 Сумматоры
- •3.9. Арифметико-логические устройства
- •3.10. Матричные умножители
- •3.11 Постановка и методы решения задач синтеза комбинационных узлов
- •3.11.1 Синтез комбинационных узлов
- •3.11.2 Основные факторы, которые должны быть учтены при построении принципиальных схем
- •3.11.2.1 Питающие напряжения ис
- •3.11.2.2 Уровни логических сигналов
- •3.11.2.3 Нагрузочная способность
- •3.11.2.4 Коэффициент объединения по входу
- •3.11.2.5 Быстродействие
- •3.11.2.6 Помехоустойчивость
- •3.11.2.7 Рассеиваемая мощность
- •3.11.2.8. Использование элементов, имеющих выходы с третьим состоянием или с открытым коллектором
- •3.12 Критерии оценки качества технической реализации кс
- •3.13 Контрольные вопросы
- •Тема 4. Схемотехника цифровых элементов Лекция 4
- •4.1 Последовательностные цифровые схемы
- •4.2. Схемотехника триггерных устройств
- •4.3. Асинхронные триггеры
- •4.4. Синхронные триггеры
- •Rs триггер с синхронизацией по уровню
- •Синхронный rs триггер с синхронизацией по фронту
- •4.5 Методы построения триггеров одного типа на базе триггеров другого типа
- •Проектирование триггеров на основе rs-триггера
- •Метод преобразования характеристических уравнений
- •Метод сравнения характеристических уравнений
- •Использование jk-триггера
- •4.6 Регистры и регистровые файлы
- •4.6.1 Регистры памяти
- •4.6.2 Сдвигающие регистры
- •4.6.3 Универсальные регистры
- •4.7 Счётчики
- •4.7.1 Счетчики с непосредственными связями и последовательным переносом
- •4.7.2 Счетчики с параллельным переносом
- •4.7.3 Реверсивный счетчик с последовательным переносом
- •4.7.4 Двоично-кодированные счётчики с произвольным модулем
- •Построение счетчика методом модификации межразрядных связей
- •Построение счетчика методом управления сбросом
- •4.8 Распределители тактов
- •4.8.1 Распределители импульсов и распределители уровней
- •4.8.2 Кольцевой регистр сдвига
- •4.8.3 Счётчик Джонсона
- •4.9 Контрольные вопросы
- •Тема 5. Схемотехника цифровых узлов Лекция 5
- •5.1 Цифровые автоматы и их разновидности
- •5.2 Абстрактный и структурный автоматы
- •5.3. Способы описания и задания автоматов
- •5.4. Связь между моделями Мура и Мили
- •5.5. Минимизация числа внутренних состояний полностью определенных автоматов
- •5.6. Принцип микропрограммного управления. Понятия об операционном и управляющем автоматах
- •Операционные элементы
- •5.7. Граф - схемы алгоритмов (гса) и их разновидности. Способы задания гса, требования к ним
- •5.8. Абстрактный синтез микропрограммных управляющих автоматов Мили и Мура
- •5.8.1. Синтез автомата Мили
- •5.8.2. Синтез автомата Мура
- •5.9. Структурный синтез микропрограммных управляющих автоматов Мили и Мура
- •5.9.1. Структурный синтез автомата Мили
- •5.9.2. Структурный синтез автомата Мура
- •5.10. Синтез автомата Мура на базе регистра сдвига
- •5.11. Контрольные вопросы
- •Тема 6. Интегрированные системы элементов Лекция 6. Программируемые логические устройства
- •6.1 Основные физические принципы программирования плм и плис
- •6.1.1 Метод плавких перемычек
- •6.1.2 Метод наращиваемых перемычек
- •6.1.3 Устройства, программируемые фотошаблоном
- •6.1.4 Стираемые программируемые постоянные запоминающие устройства
- •6.1.5. Электрически стираемые программируемые постоянные запоминающие устройства
- •6.1.6. Flash - технология
- •6.1.7. Статическое оперативное запоминающее устройство
- •6.1.8. Сравнительная таблица технологий программирования
- •6.2 Простые и сложные плу
- •6.2.1 Ппзу
- •6.2.2 Программируемые логические матрицы
- •6.2.3. Программируемые матрицы pal и gal
- •6.2.4 Дополнительные программируемые опции
- •6.2.5 Сложные плу
- •6.3. Контрольные вопросы
- •Лекция 7. Программируемые логические интегральные схемы
- •7.1 Мелко-, средне- и крупномодульные архитектуры
- •7.2 Логические блоки на мультиплексорах и таблицах соответствия
- •7.3 Таблицы соответствия, распределённое озу, сдвиговые регистры
- •7.4 Конфигурируемые логические блоки, блоки логических символов, секции
- •7.5 Секции и логические ячейки
- •7.6 Конфигурируемые логические блоки clb и блоки логических массивов lab
- •7.7. Контрольные вопросы
- •Лекция 8
- •8.1 Дополнительные встроенные функции
- •8.1.1 Схемы ускоренного переноса
- •8.1.2 Встроенные блоки озу
- •8.1.3 Встроенные умножители, сумматоры и блоки умножения с накоплением
- •8.1.4 Аппаратные и программные встроенные микропроцессорные ядра
- •8.2 Дерево синхронизации и диспетчеры синхронизации
- •8.2.1 Дерево синхронизации
- •8.2.2 Диспетчер синхронизации
- •8.3. Системы с перестраиваемой архитектурой
- •8.4. Программируемый пользователем массив узлов
- •8.4.1. Технология picoArray компании picoChip
- •8.4.2 Технология адаптивных вычислительных машин компании QuickSilver
- •8.5. Контрольные вопросы
- •Тема 7. Схемотехника аналоговых узлов Лекция 9. Операционные усилители
- •9.1. Идеальный операционный усилитель
- •9.2. Основные схемы включения операционного усилителя
- •9.2.1. Дифференциальное включение
- •9.2.2. Инвертирующее включение
- •9.2.3 Неинвертирующее включение
- •9.3 Функциональные устройства на операционных усилителях
- •9.3.1 Схема масштабирования
- •9.3.2 Схема суммирования
- •9.3.3 Схема интегрирования
- •9.3.4 Схема дифференцирования
- •9.3.5 Источники напряжения, управляемые током
- •9.3.6 Источники тока, управляемые напряжением
- •9.4 Активные электрические фильтры на оу
- •9.5 Схемы нелинейного преобразования на оу
- •9.6 Генераторы сигналов на оу
- •9.7. Контрольные вопросы
- •Лекция 10
- •10.1. Изолирующие усилители
- •10.2. Аналоговые компараторы
- •10.3. Источники опорного напряжения
- •10.4. Аналоговые коммутаторы
- •10.5. Оптореле
- •10.6. Устройства выборки-хранения
- •10.7. Цифроаналоговые преобразователи
- •10.8. Аналого-цифровые преобразователи
- •10.9. Контрольные вопросы
- •Тема 8. Схемотехника обслуживающих элементов Лекция 11
- •11.1 Сопряжение цифровых микросхем, изготовленных по разным технологиям, и сопряжение с интерфейсами
- •11.2 Управление входами ттл и кмоп
- •11.3 Дискретное управление нагрузкой от элементов ттл и кмоп
- •11.4 Передача цифровых сигналов на небольшие расстояния
- •11.5 Контрольные вопросы
- •Тема 9. Источники питания. Схемотехника комбинаторных узлов Лекция 12
- •12.1. Схемотехника линейных стабилизаторов напряжения
- •12.2 Импульсные стабилизаторы напряжения
- •12.3 Инверторные схемы
- •12.4 Контрольные вопросы
- •Тема10. Цифровые компьютеры Лекция 13
- •13.1. Принципы действия цифровых компьютеров
- •13.2. Понятие о системе программного (математического) обеспечения эвм
- •13.3. Большие эвм общего назначения
- •13.3.1. Каналы
- •13.3.2. Интерфейс
- •13.4. Малые эвм
- •13.5. Контрольные вопросы
- •Тема 11. Запоминающие устройства Лекция 14
- •14.1 Структура памяти эвм
- •14.2 Способы организации памяти
- •14.2.1 Адресная память
- •14.2.2 Ассоциативная память
- •14.2.3 Стековая память (магазинная)
- •14.3. Структуры адресных зу
- •14.3.1. Зу типа 2d
- •14.3.2. Зу типа 3d
- •14.3.3. Зу типа 2d-m
- •14.4 Постоянные зу (пзу, ппзу)
- •14.5. Флэш-память
- •14.6. Контрольные вопросы
- •Тема 12. Процессоры Лекция 15
- •15.1 Операционные устройства (алу)
- •15.2 Управляющие устройства
- •15.2.1. Уу с жёсткой логикой
- •15.2.2 Уу с хранимой в памяти логикой
- •15.2.2.1. Выборка и выполнение мк
- •15.2.2.2. Кодирование мк
- •15.2.2.3. Синхронизация мк
- •15.3. Контрольные вопросы
- •Тема 13. Универсальные микропроцессоры Лекция 16. Архитектура процессора кр580вм80
- •16.1. Регистры данных
- •16.2. Арифметико-логическое устройство
- •16.3. Регистр признаков
- •16.4. Блок управления
- •16.5. Буферы
- •16.6. Мп с точки зрения программиста
- •16.7. Форматы данных в кр580вм80
- •16.8. Форматы команд в кр580вм80
- •16.9. Способы адресации
- •16.10. Контрольные вопросы
- •Лекция 17. Система команд кр580вм80
- •17.1. Пересылки однобайтовые
- •17.2. Пересылки двухбайтовые
- •17.3. Операции в аккумуляторе
- •17.4. Операции в рон и памяти
- •17.5. Команды управления
- •17.6. Контрольные вопросы
- •Тема 14. Структуры микропроцессорных систем Лекция 18. Общие принципы
- •18.1. Системный интерфейс микро-эвм. Цикл шины
- •18.2. Промежуточный интерфейс
- •18.3. Принципы организации ввода/вывода информации в микропроцессорную систему
- •18.4. Контрольные вопросы
- •Лекция 19. Принципы организации систем прерывания программ
- •19.1. Характеристики систем прерывания
- •19.2. Возможные структуры систем прерывания
- •19.3. Организация перехода к прерывающей программе
- •19.3.1. Реализация фиксированных приоритетов
- •19.3.2. Реализация программно-управляемых приоритетов
- •19.4. Контрольные вопросы
- •Лекция 20. Принципы организации систем прямого доступа в память
- •20.1. Способы организации доступа к системной магистрали
- •20.2. Возможные структуры систем пдп
- •20.3. Организация обмена в режиме пдп
- •20.3.1. Инициализация средств пдп
- •20.3.2. Радиальная структура ( Slave dma)
- •20.3.3. Радиальная структура (Bus master dma)
- •20.3.4. Цепочечная структура ( Bus master dma)
- •20.3.5. Принципы организации арбитража магистрали
- •20.4. Микропроцессорная система на основе мп кр580вм80а
- •20.5. Контрольные вопросы
- •Тема 15. Схемы поддержки мп на системных платах Лекция 21
- •21.1. Эволюция шинной архитектуры ibm pc
- •21.1.1. Локальная системная шина
- •21.1.2. Шина расширения
- •21.1.2.1. Шина расширения isa
- •21.1.2.2. Шина расширения mca
- •21.1.2.3. Шина расширения eisa
- •21.1.3. Локальные шины расширения
- •21.1.3.1. Локальная шина vesa (vlb)
- •21.1.3.2. Локальная шина pci
- •21.2. Современные схемы поддержки мп на системных платах
- •21.2.1. Чипсет GeForce 9300/9400 фирмы nvidia
- •21.2.3. Чипсет Intel z68 для платформы Socket 1155
- •21.3. Контрольные вопросы
- •Тема 16. Некоторые вопросы развития архитектуры эвм Лекция 22
- •22.1. Теги и дескрипторы. Самоопределяемые данные
- •22.2. Методы оптимизации обмена процессор-память
- •22.2.1. Конвейер команд
- •22.2.2. Расслоение памяти
- •22.2.3. Буферизация памяти
- •22.3. Динамическое распределение памяти. Виртуальная память
- •22.3.1. Виртуальная память
- •22.3.2. Сегментно-страничная организация памяти
- •22.4. Контрольные вопросы
- •Лекция 23. Защита памяти
- •23.1. Защита отдельных ячеек памяти
- •23.2. Метод граничных регистров
- •23.3. Метод ключей защиты
- •23.4. Алгоритмы управления многоуровневой памятью
- •23.5. Контрольные вопросы
- •Тема 17. Risk – процессоры Лекция 24
- •24.1. Общая характеристика risk - процессоров
- •24.2. Arm архитектура
- •24.2.1. Дополнительные технологии
- •24.2.2. Ядро arm7tdmi
- •24.2.3. Семейство arm10 Tumb
- •24.3. Контрольные вопросы
- •Тема 18. Суперкомпьютеры. Параллельные вычислительные системы Лекция 25
- •25.1. Смена приоритетов в области высокопроизводительных вычислений
- •25.2. Сферы применения многоядерных процессоров и многопроцессорных вычислительных систем
- •25.3. Классификация архитектур вычислительных систем по степени параллелизма обработки данных
- •25.4. Архитектуры smp, mpp и numa
- •25.5. Организация когерентности многоуровневой иерархической памяти
- •25.6. Pvp архитектура
- •25.7. Контрольные вопросы
- •Лекция 26. Кластерная архитектура
- •26.1. Архитектура связи в кластерных системах
- •26.2. Коммутаторы для многопроцессорных вычислительных систем.
- •26.2.1. Простые коммутаторы
- •26.2.2. Составные коммутаторы
- •26.2.2.1. Коммутатор Клоза
- •26.3. Контрольные вопросы
- •Лекция 27. Высокопроизводительные многоядерные процессоры для встраиваемых приложений
- •27.1. Процессоры Tile-64/64Pro компании Tilera
- •27.4. Мультипроцессор Cell
- •27.4.1. Общая структура процессора Cell
- •27.4.2. Структура процессорного элемента Power (ppe)
- •27.4.3. Структура spe — "синергичного" процессорного элемента
- •27.5. Альтернативная технология построения многоядерных систем на кристалле — atac
- •27.5.1. Основные идеи архитектуры atac
- •27.5.2. Ключевые элементы технологии атас
- •27.5.3. Структура межъядерных связей
- •27.5.4. Передача данных и согласование кэш-памяти
- •27.6. Контрольные вопросы
- •Список литературы
5.5. Минимизация числа внутренних состояний полностью определенных автоматов
Рассмотрим метод минимизации полностью определенных автоматов, предложенный Ауфенкампом и Хоном.
Основная идея этого метода заключается в разбиении всех состояний исходного абстрактного автомата на попарно непересекающиеся классы эквивалентных состояний и замене каждого класса эквивалентности одним состоянием. Т.о. получающийся в результате минимальный автомат имеет столько состояний, на сколько классов эквивалентности разбиваются состояния исходного автомата.
Для пользования методом введем несколько определений.
Два состояния абстрактного автомата называются 1-эквивалентными в том случае, если реакции автомата в этих состояниях на всевозможные входные слова совпадают.
Объединение всех 1-эквивалентных состояний абстрактного автомата образует 1-класс эквивалентности.
1-эквивалентные состояния автомата называются 2-эквивалентными, если они переводятся любым входным сигналом также в 1-эквивалентные состояния.
Объединение всех 2-эквивалентных состояний образует 2-класс эквивалентности.
По индукции можно распространить определение до i-эквивалентных состояний и i-классов эквивалентности.
Если для некоторого i разбиения состояний автомата на ( i +1) - классы совпадает с разбиением на i-классы, то оно является разбиением и на - классы эквивалентности.
Разбиение множества внутренних состояний автомата на - классы и является требуемым разбиением на классы эквивалентности, при этом такое разбиение может быть получено за конечное число шагов.
Все вышеизложенное непосредственно применимо к минимизации автомата Мили. При минимизации полностью определенных автоматов Мура вводится понятие 0-эквивалентности состояний и разбиение множества состояний на 0-эквивалентные классы: к такому классу относятся одинаково отмеченные состояния автомата Мура.
Если два 0-эквивалентных состояния любым входным сигналом переводится в два 0-эквивалентных состояния, то они называются 1-эквивалентными. Все дальнейшие классы эквивалентности состояний для автомата Мура определяются аналогично приведенному для автоматов Мили.
Рассмотрим пример минимизации автомата Мили, заданного таблицами переходов и выходов – таблицы 5.7.
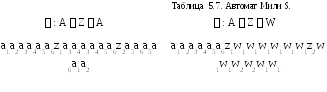
Из таблицы выходов получаем разбиение на 1-классы эквивалентности 1, объединяя в эквивалентные классы Bi состояния с одинаковыми столбцами: 1 = {B1, B2}; B2 = {a1, a2, a5, a6}; B2 = {a3, a4}. Для получения 2-эквивалентных состояний строим таблицу 1-разбиения (табл.5.8), заменяя в таблице переходов состояния a1 соответствующими классами эквивалентности B1 или B2.
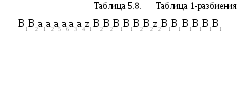
Из полученной таблицы 1-разбиения получаем 2-классы эквивалентности Ci и разбиение 2 = {C1, C2, C3}, где С1 = {a1, a2}, C2 = {a5, a6}, C3 = {a3, a4}. Сравнивая 2 и 1, отмечаем, что эти разбиения отличаются друг от друга. Поэтому аналогично строим таблицу 2-разбиения (табл. 5.9), опять заменяя в таблице переходов состояния ai соответствующими классами эквивалентности Ci.
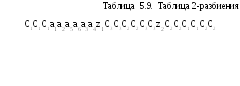
Из полученной таблицы 2-разбиения получаем 3-классы эквивалентности Di и разбиение 3 ={ D1, D2, D3}, где D1 = {a1, a2}, D2 = {a5, a6}, D3 = {a3, a4}.
Сравнивая 3 и 2, замечаем, что D1 = C1, D2 = C2, D3 = C3, 3 = 3. Следовательно получили разбиение на - эквивалентные классы. Т.к. всего три таких класса, то минимальный автомат будет содержать всего три состояния. Выбираем из каждого класса Di по одному состоянию и получаем множество состояний A' минимального автомата. Пусть, например, A'={à1, à4, à5}. Для получения минимального автомата из первоначальных таблиц переходов и выходов (табл. 5.7) вычеркиваем столбцы, соответствующие "лишним состояниям" a2, a3, a6. В результате получается минимальный автомат Мили, эквивалентный исходному автомату (табл. 5.10).
Табл.5.10. Таблицы переходов и выходов минимального автомата
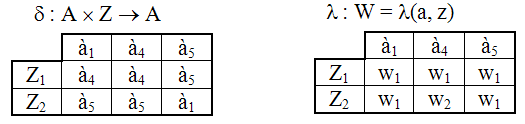
Минимизацией числа внутренних состояний автомата заканчивается этап абстрактного синтеза.
