
Курс теоретической механики 2007 (Рус)
.pdf
Аналогично, проектируя равенство (14) на оси координат, будем иметь
& |
&& |
& |
&& |
& |
&& |
(20) |
ax = Vx |
= x, ay |
= Vy |
= y, az |
= Vz |
= z , |
т.е. проекции ускорения точки на оси координат равны вторым
производным соответствующих координат по времени.
Абсолютная величина ускорения определяется по формуле
a = |
2 |
2 |
2 |
= |
&&2 |
&&2 |
&&2 |
, |
(21) |
ax |
+ ay |
+ az |
x |
+ y |
+ z |
а направление определяется направляющими косинусами
cos(x, a) = |
|
ax |
= |
|
|
|
|
&x& |
|
|
|
|
, |
||||
|
a |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
&&2 |
&&2 |
&&2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x |
+ y |
+ z |
|||||
cos(y,a) = |
ay |
|
= |
|
|
|
|
&y& |
|
|
|
|
, |
||||
a |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
&&2 |
&&2 |
&&2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x |
+ y |
+ z |
|||||
cos(z, a) = |
az |
|
= |
|
|
|
|
&z& |
|
|
. |
||||||
|
|
|
|
|
|
|
|
||||||||||
a&x&2 + &y&2 + &z&2
§7. Определение скорости при естественном способе задания
движения точки
Запишем формулу (10) в следующем виде:
Vcp = |
MM |
1 |
s |
|
|
|
. |
(22) |
|
s |
|
|||
|
|
t |
|
Предел отношения длины хорды | MM1 |
к длине стягиваемой ею дуги кривой s (рис.8) равен единице при s→0, а предельное положение секущей совпадает с положением касательной, то
lim |
MM1 |
= τ , |
(23) |
|
|||
s→0 |
s |
|
|
где τ – единичный вектор (орт) касательРис.8 ной к кривой, направленной в сторону возрастания натуральной координаты s.
61

Учитывая, что s→0 при t→0, получаем
V = lim V |
|
= lim |
MM1 |
lim |
|
cp |
|
||||
t→0 |
s→0 |
s |
t→0 |
||
|
|||||
Из (24) следует, что |
|
|
|
|
Vτ = ds , dt
s |
= |
ds |
τ. |
(24) |
|
|
|||
t |
|
dt |
|
|
(25)
где Vτ - проекция скорости на направление касательной. Заметим, что
Vτ = ±V, |
(26) |
где знак плюс ставится в случае совпадения направления скорости и положительного направления касательной и знак минус в противном случае. Поэтому проекция скорости на направление касательной Vτ носит еще название алгебраической величины скорости. Тогда (24) запишется так:
V = Vτ τ |
(27) |
Алгебраическая величина скорости равна производной натуральной координаты по времени. Если алгебраическая
величина скорости положительна, то направление скорости совпадает с направлением касательной, в противном случае – направление скорости противоположно направлению касательной.
§ 8. Кривизна линии
Углом смежности θ отрезка кривой ММ1 называется угол между двумя касательными к этой кривой – в начале М и конце М1
рассматриваемого отрезка (рис.9). |
|
|
|
|
|
|
|
|
Средней кривизной линии на отрезке |
||||||
|
называется |
|
|
|
отношение |
угла |
|
|
смежности к длине дуги этого |
||||||
|
отрезка: |
|
|
|
|
|
|
|
|
k |
|
= |
θ |
. |
(28) |
|
|
cp |
|
||||
|
|
|
|
s |
|
||
|
|
|
|
|
|
||
|
Кривизной линии в точке М называет- |
||||||
Рис.9 |
ся предел |
средней кривизны примы- |
|||||
|
кающего к этой точке отрезка ММ1 |
||||||
62
кривой при стремлении длины дуги отрезка к нулю:
k = lim k |
|
= |
lim |
θ |
. |
(29) |
cp |
|
|||||
s→0 |
|
s→0 |
s |
|
||
|
|
|
||||
Радиусом кривизны линии называется величина , обратная
кривизне: |
ρ = |
1 |
. |
(30) |
|
||||
|
|
k |
|
|
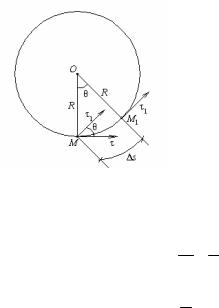
Кривизна окружности. В качестве примера найдем кривизну окружности (рис.10). Заметим, что угол смежности дуги ММ1 окружности и центральный угол МОМ1 , опирающийся на эту дугу, равны друг другу как углы с взаимно перпендикулярными сторонами. Поэтому между длиной дуги ММ1 и углом смежности θ существует зависимость
Рис.10
s = θR .
Тогда средняя кривизна на отрезке ММ1 равна
kcp = θ = 1 ,
sR
которая не зависит от длины дуги s. Поэтому в пределе получаем
k = 1 . R
Отсюда следует, что для окружности ρ = R . Таким образом,
кривизна окружности одинакова во всех ее точках и равна величине, обратной радиусу. Радиус кривизны окружности равен ее радиусу.
§ 9. Естественный трехгранник
Пусть τ – касательная, проведенная в некоторой точке М пространственной кривой (рис.11). Проведем касательную τ1 в точке М1 , расположенную недалеко от точки М (мы будем называть ее соседней точкой). Проведем через касательную τ плоскость П, параллельную касательной τ1 . При стремлении точки М1 к точке М плоскость будет поворачиваться вокруг неподвижной касательной τ.
Предельное положение плоскости, проведенной через касательную в данной точке параллельно касательной в соседней
63
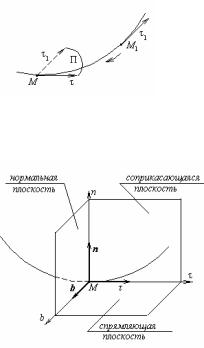
точке, при стремлении соседней точки к данной называется соприкасающейся плоскостью к кривой в данной точке.
Заметим, что если кривая лежит в плоскости (как например, окружность или парабола), то соприкасающаяся
|
плоскость совпадает с этой плоскостью. |
|||||
|
|
Очевидно, касательная к кривой ле- |
||||
|
Рис.11 |
жит в соприкасающейся плоскости. |
|
|||
|
|
Ось, проходящая через точку М, |
||||
лежащая в соприкасающейся плоскости и направленная |
в |
|||||
сторону |
вогнутости |
кривой, |
называется |
главной |
||
|
|
нормалью (на рис.12 она обозна- |
||||
|
|
начена буквой п). |
|
|
|
|
|
|
Ось, |
перпендикулярная со |
|||
|
|
прикасающейся плоскости, на- |
||||
|
|
прав –ленная в ту сторону, |
||||
|
|
откуда виден поворот от оси |
||||
|
|
τ к оси п на 90о происходящим |
||||
|
|
против |
часовой |
|
стрелки, |
|
|
|
называется бинормалью |
(на |
|||
|
|
рис.12 она обозначена буквой b). |
||||
|
|
Плоскость, |
проходящая |
|||
|
|
через |
главную |
нормаль |
и |
|
|
бинормаль, называется нор- |
|
Рис.12 |
мальной. |
|
|
Плоскость, |
проходящая |
через касательную и бинормаль, называется спрямляющей.
Три плоскости – соприкасающаяся, нормальная и спрямляющая
– образуют естественный трехгранник.
§ 10. Производная орта касательной по натуральной координате
Орт касательной τ зависит от направления касательной в точке М, положение которой определяется натуральной координатой s. Таким образом, орт касательной является функцией натуральной координаты: τ = τ (s). Обозначим через τ1 орт касательной, проведенной в точке М1 кривой с натуральной координатой s1 = s + s, т.е.
τ1 = τ ( s + s ).
64
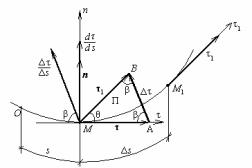
Приращение вектор-функции τ (s ) вектор |
τ = τ1 |
– |
τ лежит в |
|||||
плоскости П, проведенной через касательную τ |
параллельно |
|||||||
|
касательной τ1 (рис.13). |
|||||||
|
В |
этой |
же |
|
плоскости |
|||
|
находится и вектор Δτ . |
|||||||
|
|
|
|
|
|
|
|
s |
|
Вектор |
|
|
|
|
|||
|
|
|
dτ |
= lim |
|
τ |
||
|
|
|
|
|
|
|
||
|
|
|
ds |
s→0 |
|
s |
||
|
лежит в предельной, т.е. |
|||||||
|
в |
|
соприкасающейся |
|||||
|
плоскости. В |
|
равнобед- |
|||||
|
ренном |
треугольнике |
||||||
|
АМВ угол β = 90о – θ/2 |
|||||||
Рис.13 |
стремится к 90о , так как |
|||||||
θ → 0 при s → 0. Следовательно, предельный вектор dτ/ds перпендикулярен касательной, т.е. направлен вдоль главной нормали, причем в положительном ее направлении. Остается найти его величину. Из треугольника АМВ имеем
|
dτ |
|
= lim |
|
τ |
|
= lim |
2sin |
θ |
|
lim |
θ |
= k , |
||
|
|
|
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
ds |
|
s→0 |
s |
θ→0 |
θ |
|
|
|
s→0 s |
|
||||
так как θ → 0 при |
s → 0 и |
lim |
sin φ |
=1 |
(первый замечательный |
||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
φ→0 |
|
|
|
φ |
|
||
предел).
Учитывая и величину, и направление вектора dτ/ds, можно
записать |
|
|
|
|
|
|
dτ |
= kn = |
1 |
n , |
(31) |
|
|
|
|||
|
ds |
|
ρ |
|
|
где n – орт главной нормали.
§ 11. Определение ускорения при естественном способе задания движения точки
Дифференцируя (27) по времени, получаем
65

a = |
dVτ |
τ +Vτ |
dτ |
, |
(32) |
dt |
|
||||
|
|
dt |
|
||
Представим dτ/dt в следующем виде:
|
|
dτ |
= |
dτ |
|
ds |
= |
Vτ |
n |
(33) |
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
dt ds dt |
|
|
ρ |
|
|||||||
|
(здесь |
|
использованы |
||||||||||
|
формулы (25) и (31)). |
||||||||||||
|
|
|
Подставив (33) в (32), |
||||||||||
|
находим |
|
|
|
|
|
|
||||||
|
|
|
a = |
dVτ |
|
τ + |
V 2 |
n , |
|||||
|
|
|
|
|
ρ |
||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|||
Рис.14 |
так как Vτ2 = V 2 . Таким об- |
||||||||||||
|
разом, |
|
|
|
|
|
|
||||||
ускорение равно геометрической сумме двух составляющих:
а = aτ + an , |
(34) |
||||||
вдоль касательной |
|
|
|
|
|
|
|
aτ |
= |
|
dVτ |
|
τ |
(35) |
|
dt |
|
||||||
|
|
|
|
|
|
||
и вдоль главной нормали |
|
|
|
|
|
|
|
an |
= |
V 2 |
|
n . |
(36) |
||
|
|||||||
|
|
|
ρ |
|
|
|
|
Проекции ускорения на касательную (касательное ускорение) и главную нормаль (нормальное ускорение) определяются по формулам
|
aτ |
= |
dVτ |
, |
an |
= |
V 2 |
. |
|
|
|
(37) |
||||||
|
|
dt |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
Величина ускорения равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
dVτ 2 |
|
V 2 |
2 |
|
||||||||
|
2 |
2 |
|
|
|
|||||||||||||
a = |
aτ + an = |
|
|
|
|
|
+ |
|
|
|
. |
(38) |
||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
ρ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
66

§12. Некоторые частные случаи движения точки
1.Равномерное движение.
Равномерным называется движение точки с постоянной алгебраической скоростью.
Таким образом,
Vτ |
= |
ds |
= const . |
|
|
|
|||
|
|
dt |
|
|
Отсюда находим ds = Vτ dt |
и, интегрируя, получаем |
|
||
|
s = Vτt + so |
(39) |
||
(so – натуральная координата движущейся точки при t = 0), т.е.
закон равномерного движения точки представляет собой линейную функцию времени.
Найдем касательное ускорение точки
aτ = dVτ = 0 , т.е. dt
касательное ускорение точки при равномерном движении равно нулю.
2.Равнопеременное движение точки.
Равнопеременным |
|
называется |
движением |
точки |
с |
||||||
постоянным касательным ускорением, т.е. |
|
|
|||||||||
|
|
|
aτ |
= |
dVτ |
= const |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
dt |
|
|
|
|
Отсюда dVτ = aτ dt , и после интегрирования получаем |
|
|
|||||||||
|
|
|
Vτ |
= aτt +Voτ |
|
(40) |
|
||||
(Voτ – значение Vτ при t = 0). |
|
|
|
|
|
|
|||||
Подставляя Vτ |
= |
ds |
в (40) и интегрируя, получаем |
|
|
||||||
|
|
|
|||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
s = |
aτt 2 |
|
+Voτt + so . |
|
(41) |
|
||
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
||
Таким образом, |
|
закон |
равнопеременного движения точки |
||||||||
представляет собой квадратичную функцию времени.
Заметим, что если aτ > 0, то движение точки называется равноускоренным, если же aτ < 0, движение точки называется
равнозамедленным.
67
§13. Примеры
1.Определение скорости и ускорения точки при координатном способе задания движения.
Даны уравнения движения точки
x = 2cos2t + 3 (м); y = 4sin 2t (м) ( t – в секундах)
Необходимо найти уравнение траектории и построить ее на чертеже, а также для момента времени t = π / 4 с найти положение движущейся точки М, скорость и ускорение ее и построить их на чертеже. Кроме того, необходимо найти касательное и нормальное ускорения точки М, а также радиус кривизны траектории в том месте, где находится точка
М.
Решение. Для определения уравнения траектории точки необходимо исключить параметр t из уравнений движения. Используем основное тригонометрическое тождество
sin2 2t + cos2 2t = 1
Из первого уравнения движения имеем cos2t = x − 3 , а из второго
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
sin 2t = |
y |
. Подставляя эти выражения в основное |
тригонометри- |
||||||||||||
|
|||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ческое тождество, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(x − 3) |
2 |
+ |
y |
2 |
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
22 |
|
42 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
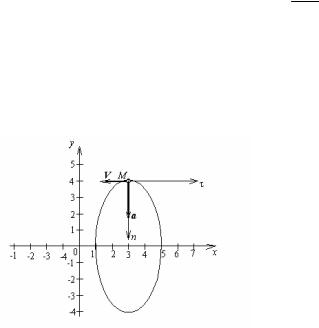
Это уравнение эллипса, |
|
полуоси которого |
соответственно |
|||||||||||
|
|
|
|
|
|
|
|
равны 2м и 4м, а центр |
|||||||
|
|
|
|
|
|
|
|
находится в |
точке |
x = |
|||||
|
|
|
|
|
|
|
|
3м, |
y = 0. Таким обра- |
||||||
|
|
|
|
|
|
|
|
зом, траекторией движе- |
|||||||
|
|
|
|
|
|
|
|
ния |
точки |
является |
|||||
|
|
|
|
|
|
|
|
эллипс. Строим его |
на |
||||||
|
|
|
|
|
|
|
|
чертеже. |
|
В |
момент |
||||
|
|
|
|
|
|
|
|
времени |
t |
точка |
М |
||||
|
|
|
|
|
|
|
|
имеет координаты |
|
||||||
|
|
|
|
|
|
|
|
x = 2cos |
π |
+ 3 =3м, |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = 4sin |
π |
= 4 м. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
Рис.15 |
|
|
|
|
Проекции скорости точ- |
||||||||
|
|
|
|
|
|
|
|
ки М на оси координат |
|||||||
68
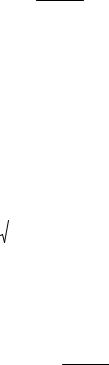
равны
Vx = x& = −4sin 2t,
Vy = y& = 8cos 2t .
При t = π/4 с они принимают следующие значения:
Vx = −4sin(π / 2) = − 4 м/с
Vy = 8cos(π / 2) = 0 .
Модуль скорости равен
V = 
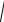 Vx2 +Vy2 = 4м / с .
Vx2 +Vy2 = 4м / с .
На чертеже строим составляющие скорости Vx и Vy ,
параллельные осям координат и имеющие найденные выше величины. Вектор V равен геометрической сумме Vx и Vy . В рассматриваемом
случае V = Vx .
Проекции ускорения точки М на оси координат равны
ax = &x& = −8cos2t, ay = &y& = −16sin 2t .
|
|
При |
t = π / 4 с |
они |
|
|
принимают |
следующие |
значения: |
|
a |
x |
= −8cos(π / 2) = 0 , |
|
a |
Y |
= −16sin(π / 2) = −16м / с2 . |
Модуль |
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||||
ускорения равен a = |
a2 + a2 |
= 16м / с2 . |
|
|
||||||
|
|
|
|
x |
y |
|
|
|
|
|
|
|
На |
чертеже строим |
составляющие |
ускорения ax |
и ay , |
||||
параллельные осям координат и имеющие найденные выше величины. Вектор a равен геометрической сумме ax и ay . В рассматриваемом
здесь случае a = ay . Дифференцируя формулу
V = 
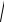 Vx2 +Vy2
Vx2 +Vy2
по времени и используя (37) и (20), находим, что
aτ = (Vxax + Vxay ) /V .
69

В рассматриваемом случае aτ = [−4 0 + 0 (−16)]/ 4 = 0 .
Нормальное ускорение определяется по формуле a |
n |
= |
a2 − a2 |
|||||||
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
В нашем случае |
a |
n |
= 162 − 0 = 16м / с2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Радиус кривизны находим по формуле ρ = V 2 / a |
n |
, т.е. ρ = 42 /16 =1м. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
2. Определение скорости и ускорения точки при естественном способе задания движения.
Пример. Точка М движется по траектории, изображенной на рисунке.
Длина прямолинейного отрезка l=4π м, радиус криволинейной части траектории R=8м. Закон движения точки по
траектории |
s = 2πt2 м. |
|
Необходимо найти |
положение |
|
точки, |
скорость, |
касательное, |
нормальное и полное ускорения точки при t=1c и при t=2с.
Рис.16
Решение. Находим положение точки при t=1с. Для этого подставляем это значение в закон движения. Получаем s = 2π = l / 2 . Таким образом, точка находится посредине прямолинейного участка траектории.
Находим алгебраическую величину скорости по формуле
ds
Vτ = dt = 4πt .
При t=1с получаем V =|Vτ |= 4π м/с. Так как точка движется вдоль прямой линии, то нормальное ускорение ее равно нулю: an = 0 и полное ускорение совпадает с касательным:
a =| a |
|
|=| |
dVτ |
| , |
|
τ |
dt |
||||
|
|
|
|||
|
|
|
|
70
