Курс теоретической механики 2007 (Рус)
.pdf
т.е. a = 4π м/с2.
При t=2с получаем s = 8π м. Так как длина прямолинейного участка l=4π м, то очевидно, что точка оказывается на криволинейном участке, при этом ее расстояние от начала этого участка равно s − l = 4π м. Длина полуокружности равна πR=8π м, таким образом точка оказывается посередине полуокружности. Величина скорости равна V = 8π м/с. Касательное ускорение
aτ = dVτ = 4π м/с2. dt
Нормальное ускорение
an = V 2 / R = 8π2 м/с2.
Полное ускорение точки определяется по формуле
a = 
aτ2 + an2 = 
16π2 + 64π4 = 79,95 м/с2.
Векторы V, aτ ,an и a показаны на рисунке.
71
Г Л А В А II
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
§ 1. Поступательное движение
Движение тела называется поступательным, если любая прямая, проведенная в этом теле, остается параллельной своему
первоначальному положению.
Теорема. При поступательном движении точки тела описывают одинаковые траектории (т.е. которые могут быть совмещены) и в каждый момент времени точки тела имеют геометрически равные скорости и геометрически равные
ускорения.
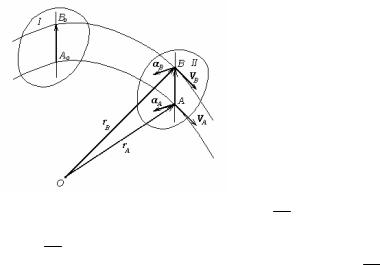
Доказательство. Пусть при t = 0 тело занимало положение I, а в момент времени t – положение II (рис.17). Проведем через две точки А и В в начальном положении тела прямую (на чертеже они обозначены через Ао и Во). В процессе движения ее направление остается неизменным, так как она остается параллельной своему первоначальному положению. Кроме того, длина отрезка АВ остается неизменной, так как точки А и В являются точками абсолютно твердого тела. Отсюда
следует , что
Рис.17 AB = const . (42) Если переместить точку А на
вектор AB , то она совместится с точкой В. Поскольку это справедливо
для любого момента времени, то при смещении на вектор AB вся траектория точки А совместится с траекторией точки В. Так как точки А и В – произвольные точки тела, то отсюда следует, что все точки
тела описывают одинаковые траектории.
Из чертежа следует, что
72
|
|
|
|
rB = rA + AB . |
(43) |
||
Это равенство справедливо в любой момент времени, т.е. в левой и правой частях ее стоят равные вектор-функции времени.
Продифференцировав (43) по t, получим
|
|
|
|
VB =VA , |
(44) |
|
|
|
|
|
|
так как |
d AB |
= 0 . Дифференцируя (44) |
по времени, приходим к |
||
|
|||||
|
dt |
|
|||
следующему равенству: |
|
||||
|
|
|
|
aB = aA . |
(45) |
Так как А и В – произвольные точки тела, то можно сделать вывод, что в каждый момент времени точки тела имеют геометрически
равные скорости и геометрически равные ускорения.
Следствие. Поступательное движение тела определяется движением одной точки этого тела.
Действительно, точки тела движутся по одинаковым траекториям и из-за равенства скоростей и ускорений в каждый момент времени они движутся одинаково вдоль этих траекторий.
Поэтому уравнения поступательного движения тела имеют следующий вид:
xA = f1 (t), yA = f2 (t), z A = f3 (t) |
(46) |
где А – одна из точек тела.
§ 2. Вращение тела вокруг неподвижной оси
Вращением тела вокруг неподвижной оси называется такое движение тела, при котором по крайней мере две точки тела остаются неподвижными (рис.18).
Прямая, проходящая через неподвижные точки, называется осью вращения.
Двугранный угол между двумя плоскостями, проходящими через ось вращения, одной – неподвижной, и другой – подвижной, жестко связанной с телом, взятый с учетом знака, называется угловой координатой. Угловой координате φ приписывается знак
«плюс», если с положительного направления, выбранного на оси
73
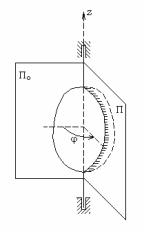
вращения, поворот на угол φ от неподвижной По к подвижной плоскости П виден происходящим против часовой стрелки, и знак
« минус» в противном случае.
Угловая координата измеряется в радианах.
Если задать угловую координату как функцию времени, то положение тела будет определено в любой момент времени. Поэтому
уравнение |
|
φ = f ( t ), |
(47) |
называется уравнением вращения твердого тела вокруг неподвижной оси.
Пусть за некоторый промежуток времени t угловая координата φ получила приращение Δφ. Отношение Δφ/Δt называется средней угловой скоростью тела за промежуток времени t. Угловой скоростью тела в момент времени t называется предел средней угловой скорости при t стремящемся к нулю:
ω = lim |
φ |
= |
dφ |
, |
|
|
|||
t→0 |
t dt |
|||
т.е. угловой скоростью вращения тела вокруг неподвижной оси
называется производная угловой координаты по времени.
Угловая скорость измеряется в рад/сек. Аналогично, угловым ускорением называется предел отношения приращения угловой скорости Δω к промежутку
времени t при t→0:
ε = lim |
ω |
= |
dω |
, |
|
|
|||
t→0 |
t dt |
|||
т.е. угловым ускорением вращения тела
вокруг неподвижной оси называется производная угловой скорости по времени.
Угловое ускорение измеряется в
рад/сек2.
Рис.18
74
§ 3. Некоторые частные случаи вращения тела вокруг неподвижной оси
1. Равномерное вращение.
Вращение тела называется равномерным, если его угловая скорость постоянна, т.е.
ω = dφ = const . dt
Отсюда находим, что dφ = ωdt и, интегрируя, получаем
φ = ωt + φo |
(48) |
(φo – угловая координата вращающегося тела при t = 0), т.е.
закон равномерного вращения тела представляет собой линейную функцию времени.
Определим угловое ускорение тела
ε = dω = 0 , т.е. dt
при равномерном вращении угловое ускорение тела равно нулю.
2.Равнопеременное вращение тела.
Равнопеременным называется вращение тела с постоянным угловым ускорением, т.е.
ε = dω = const dt
Отсюда dω = εdt , и после интегрирования получаем |
|
||||
|
|
ω = εt + ωo |
(49) |
||
(ωо – значение ω при t = 0). |
|
|
|||
Подставляя ω = |
dφ |
в (49) и интегрируя, находим |
|
||
|
|
||||
|
dt |
|
|
||
|
φ = |
εt 2 |
+ ωot + φo . |
(50) |
|
|
|
||||
2 |
|
|
|||
75
Таким образом, закон равнопеременного вращения тела
представляет собой квадратичную функцию времени.
Если ε > 0, вращение тела называется равноускоренным, если же ε < 0, вращение тела называется равнозамедленным.
§ 4. Скорости и ускорения точек вращающегося тела
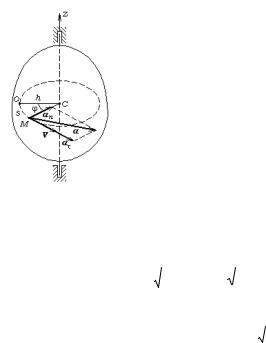
Точка М тела, вращающегося вокруг неподвижной оси, движется по окружности, центр которой С находится на оси вращения(рис.19). Пусть расстояние от точки до оси вращения, т.е. радиус окружности, по которой движется точка, равен h. Обозначим через О точку пересечения окружности с неподвижной плоскостью, а подвижную плоскость проведем через радиус СМ. Тогда угол ОСМ будет равен угловой координате φ, а положение точки М на окружности можно задать с помощью натуральной координаты s, равной длине дуги окружности ОМ. Если задано уравнение вращения тела (47), то соотношение
s = hφ
задает закон движения точки М по окружности при естественном способе задания движения. Алгебраическая величина скорости
|
определяется по формуле |
|
||||||||||||||||
|
|
|
|
Vτ |
= |
ds |
= h |
dφ |
= hω |
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
dt |
|
dt |
|
|||||||
|
Касательное и нормальное ускорения точки |
|||||||||||||||||
|
находим из формул |
|
|
|
|
|
|
|
||||||||||
|
aτ = |
dVτ |
= h |
dω |
= hε, an = |
V 2 |
= hω2 |
|||||||||||
|
|
|
|
ρ |
||||||||||||||
|
|
|
dt |
|
dt |
|
|
|
|
|
||||||||
Рис.19 |
(так как для окружности ρ = h ). Полное уско- |
|||||||||||||||||
|
рение точки определяем по формуле |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
a = aτ2 + an2 = h ε2 + ω4 . |
|
||||||||||||||||
Таким образом, формулы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||||||
Vτ |
= hω, aτ = hε, an = hω2 , a = h |
|
ε2 + ω2 |
(51) |
||||||||||||||
76
определяют скорость и ускорение точки тела, вращающегося вокруг неподвижной оси.
§ 5. Первая формула Эйлера
Введем понятие угловой скорости как вектора.
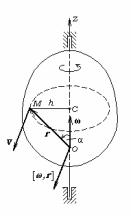
Вектором угловой скорости тела, вращающегося вокруг неподвижной оси, называется вектор, равный по модулю абсолютной величине производной угловой координаты по времени и направленный вдоль оси вращения в ту сторону, откуда видно вращение тела вокруг оси происходящим против часовой стрелки
(рис.20).
Теорема. Скорость точки тела, вращающегося вокруг неподвижной оси, равна векторному произведению угловой скорости тела на радиус-вектор точки, проведенный из полюса, лежащего на оси:
|
V = [ω, r] |
(52) |
(формула (52) и представляет собой первую формулу Эйлера). |
|
|
Доказательство. |
|
|
Величина вектора V определяется по формуле |
|
|
|
V =| ω|h, |
(53) |
а величина вектора [ω,r] вычисляется так: |
|
|
|
|[ω,r]|=|ω||r|sin α, |
(54) |
|
так как |ω|=|dφ/dt|. Из треугольника ОМС |
|
|
находим |
|
|
|r|sin α = h. |
|
|
Подставив это в (54), получим |
|
|
|[ω,r]|=|ω|h. |
(55) |
|
Из (53) и (55) следует, что |
|
|
V =|[ω,r]|. |
(56) |
|
Вектор V направлен по касательной к окруж- |
|
Рис.20 |
ности, плоскость которой перпендикулярна |
|
77
оси, поэтому этот вектор перпендикулярен оси, а кроме того, перпендикулярен радиусу окружности СМ. Таким образом вектор V перпендикулярен плоскости ОМС. Вектор [ω,r] перпендикулярен перемножаемым векторам, т.е. плоскости того же треугольника ОМС. Это значит, что векторы V и [ω,r] параллельны друг другу и, как нетрудно убедиться, направлены в одну сторону. Учитывая (56), приходим к выводу, что первая формула Эйлера (52) верна.
§ 6. Пример решения задачи на вращение тел вокруг неподвижной оси
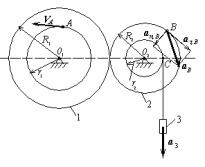
На рис.21 изображен плоский механизм, состоящий из двух находящихся в зацеплении зубчатых колес с радиусами R1 и R2 и с выступами, имеющими радиусы r1 и r2 соответственно, а также груза, подвешенного на веревке, намотанной на выступ второго колеса. Заданы закон вращения первого колеса
|
φ |
1 |
= 3t3 |
, радиусы колес и |
|
|
|
|
|
Рис.21 |
выступов R1=50 см, r1= 30 см, |
|||
R2= 40 см, r2=20 см. Необходимо определить угловую скорость колеса 1, скорость точки А, находящейся на ободе выступа колеса 1, угловое ускорение колеса 2,
а также ускорения точки В на ободе второго колеса и груза 3 при t=2 c.
Решение. Находим сначала угловую скорость и угловое ускорение
колеса 1: |
|
|
|
|
|
|
ω1 |
= |
dφ1 |
= 9t 2 (c−1 ), ε1 |
= |
dω1 |
=18t (c−2 ) . |
|
|
|||||
|
|
dt |
|
dt |
||
При t=2с имеем ω1 = 36 с-1, ε1 =36 с-2. Скорость точки А определяется по формуле
VA = ω1r1 = 36 30 = 1080 см/с.
Для того чтобы найти угловые скорость и ускорение колеса 2 необходимо воспользоваться соотношениями
78
ω1 = R2 , ε1 = R2 .
ω2 R1 ε2 R1
Отсюда получаем ω2 = ω1R1 / R2 = 36 50/ 40 = 45с-1,
ε2 = ε1R1 / R2 = 45 с-2.
Касательное и нормальное ускорения точки В находим из формул
aτ,B = ε2 R2 = 45 40 = 1800 см/с2, an,B = ω22 R2 = 452 40 =81000см/с2
Полное ускорение точки В равно
aB = 
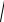aτ2,B + an2,B =81020см/с2
Ускорение груза 3 равно касательному ускорению точки С обода малого колеса 2:
a3 = aτ,C = ε2r2 = 45 20 = 900см / с2 .
79
Г Л А В А III
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 1. Основные определения
Движение точки называется сложным, если оно рассматривается относительно нескольких систем отсчета, одна из которых считается неподвижной, а остальные – движущимися по отношению к ней.
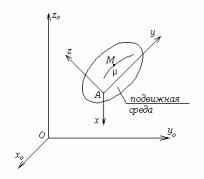
Мы ограничимся рассмотрением случая двух систем отсчета (рис.22). На этом рисунке xоyоzо – неподвижная система отсчета, xyz – подвижная система отсчета, М – движущаяся точка. Каждая система отсчета связана с некоторым телом.
Тело, с которым связана подвижная система отсчета, будем называть подвижной средой. Точка µ на рис.22 – это
Рис.22 точка подвижной среды, с которой в данный момент времени
совпадает движущаяся точка М.
Движение точки относительно неподвижной системы отсчета называется абсолютным.
Движение точки относительно подвижной системы отсчета называется относительным.
Движение подвижной системы отсчета относительно неподвижной называется переносным.
Определения абсолютной, относительной и переносной скоростей и соответствующих ускорений совершенно аналогичны. Поэтому эти определения совмещены. Отличия в определениях ускорений помещены в скобках.
Абсолютной скоростью Va (абсолютным ускорением aa) точки называется скорость (ускорение) точки относительно неподвижной системы координат.
Относительной скоростью Vr (относительным ускорением ar)
80