
Курс теоретической механики 2007 (Рус)
.pdf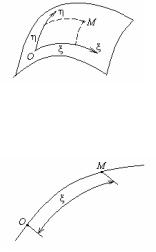
§10. Обобщенные координаты
Независимые параметры q1, q2, …,qs , однозначно определяющие
положение механической системы, называются обобщенными координатами, а их количество s − числом степеней свободы
системы.
Примеры.
1. Свободная материальная точка. Ее положение однозначно определяется тремя координатами x,y,z, т.е.
q1 = x, q2 = y, q3 = z,
ачисло степеней свободы s = 3.
2.Материальная точка, движущаяся вдоль поверхности.
Положение точки на поверхности определяется двумя криволинейными координатами ξ и η (рис.57). Таким образом,
q1 = ξ, q2 = η, s = 2.
Рис.57
3.Материальная точка, движущаяся вдоль линии. В этом
случае положение точки определяется одним параметром − натуральной координатой ξ (рис.58), т.е.
q1 = ξ, s = 1.
Рис.58
Вышеприведенные примеры являются иллюстрацией следующего факта:
181
Теорема. Наложение на механическую систему т<s
стационарных геометрических удерживающих связей уменьшают
число ее степеней свободы s на т единиц.
Доказательство. Если механическая система имеет s степеней свободы, то это означает, что ее положение однозначно определяется s независимыми параметрами qi (I = 1,2,…,s), т.е. координаты ее точек являются функциями этих параметров
xk =xk (q1 ,q2 ,…,qs ) , yk =yk (q1 ,q2 ,…,qs ) , zk =zk (q1 ,q2 ,…,qs ),
(k = 1,2,…,n) |
(192) |
(п – число точек механической системы). |
|
Пусть теперь на систему наложено дополнительно т<s
стационарных геометрических удерживающих связей |
|
|
f1 (x1 , y1 , z1 |
,…, xn , yn , zn) = 0 |
|
f2 (x1 , y1 , z1 |
,…, xn , yn , zn) = 0 |
(193) |
……………………………….. |
|
|
fm (x1 , y1 , z1 ,…, xn , yn , zn) = 0 |
|
|
Подставив равенства (192) в уравнения (193), получим |
|
|
φ1 (q1 ,q2 ,…,qs ) = 0 |
|
|
φ2 (q1 ,q2 ,…,qs ) = 0 |
(194) |
|
…………………… |
|
|
φm (q1 |
,q2 ,…,qs ) = 0 |
|
Равенства (194) можно рассматривать как систему из т алгебраических уравнений, при помощи которых т из s параметров q1,q2 ,…,qs можно выразить через остальные s−т. Таким образом, независимыми остаются только s−т параметров, а это и означает, что новое число степеней свободы s1 = s−т, что и требовалось доказать.
4. Тело, имеющее неподвижную ось вращения. В этом случае положение тела определяется одним параметром − угловой координатой φ (см. §2 главы II части II). Таким образом, для такого тела
q1 = φ, s = 1.
5.Плоская фигура, перемещающаяся в своей плоскости.
Вэтом случае три независимых параметра определяют положение
фигуры (§1 главы IV части II) − координаты х0А и у0А точки А плоской
182

фигуры и угловая координата φ, определяющая положение плоской фигуры относительно осей х и у, проходящих через точку А (рис.59).
Таким образом, для плоской фигуры
q1 = х0А , q2 = y0А , q3 = φ,
число степеней свободы s = 3.
Рис.59
6. Твердое тело, имеющее неподвижную точку. Три независимых параметра определяют положение такого тела − углы Эйлера θ, φ и ψ (§1 главы V части II). Таким образом,
q1 = θ , q2 = φ , q3 = ψ,
число степеней свободы s = 3.
7. Свободное твердое тело. Шесть независимых параметров определяют положение тела в этом случае − три координаты точки А тела и три угла Эйлера, определяющие положение тела относительно осей проходящих через эту точку (§4 главы V части II). Таким образом,
q1 = х0А , q2 = y0А , q3 = z0А, q4 = θ , q5 = φ , q6 = ψ,
число степеней свободы s = 6.
§11. Обобщенные силы
Рассмотрим механическую систему с s степенями свободы, состоящую из п материальных точек М1, М2, …, Мп , на которые действуют силы F1, F2, …, Fп . Элементарная работа сил определяется по формуле
183

n |
|
dA = ∑(Fk , drk ) . |
(195) |
k=1
Положения точек системы, а значит, и их радиус-векторы определяются значениями обобщенных координат:
rk = rk (q1 ,q2 ,…,qs ) (k = 1,2,…,n). |
(196) |
Дифференциалы функций (196) определяются по формулам
drk = ∑s ∂rk dqi (k = 1,2,…,n).
i=1 ∂qi
Подставляя их в (195) и меняя местами суммирования по k и по I, будем иметь
|
|
s |
n |
|
∂rk |
|
|
|||
|
dA = ∑dqi ∑(Fk , |
) . |
(197) |
|||||||
|
∂q |
i |
||||||||
|
i=1 |
k=1 |
|
|
|
|
|
|||
Введем обозначения |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
∂rk |
|
|
|
|
|
|
|
Qi |
= ∑(Fk , |
|
) . |
|
|
(198) |
|||
|
∂q |
i |
|
|
|
|||||
|
|
k=1 |
|
|
|
|
|
|
|
|
Тогда (197) запишется так |
|
|
|
|
|
|
|
|
||
|
|
|
s |
|
|
|
|
|
|
|
|
dA = ∑Qi dqi . |
|
|
(199) |
||||||
|
|
i=1 |
|
|
|
|
|
|
||
Величина Qi |
называется обобщенной |
|
силой, соответствующей |
|||||||
обобщенной координате qi |
(I = 1,2,…,s). Из формулы (199) следует, |
|||||||||
что обобщенная |
сила |
Qi |
, соответствующая |
обобщенной |
||||||
координате qi − это множитель при элементарном приращении
этой обобщенной координаты в выражении элементарной работы действующих на систему сил.
Примеры.
1. Свободная материальная точка. Пусть на точку действует сила F. Элементарная работа силы вычисляется по формуле
dA = Fx dx + Fy dy + Fz dz.
В соответствии с примером 1 предыдущего параграфа q1 = x, q2 = y, q3 = z. Тогда
184
dA = Fx dq1 + Fy dq2 + Fz dq3.
Сопоставляя это равенство с (199), заключаем
Q1 = Fx , Q2 = Fy , Q3 = Fz ,
т.е. обобщенные силы равны проекциям силы, действующей на
точку, на оси координат.
2. Тело, имеющее неподвижную ось вращения. В соответствии с формулой (131) §13 главы II части III имеем
dA = Mz dφ,
где Mz − сумма моментов сил, действующих на тело, относительно оси вращения. Учитывая, что q1 = φ, делаем вывод, что обобщенная сила
для тела, вращающегося вокруг неподвижной оси, является сумма моментов сил, действующих на тело, относительно оси вращения.
3. Плоская фигура, двигающаяся в своей плоскости. В
соответствии с формулой (133) (§13 главы II части III) имеем
dA = Mz dφ + (R , dΑ ), |
(200) |
n |
|
где M z = ∑mz (Fk ) , R − главный вектор плоской |
системы сил |
k=1 |
|
{F1,F2,…,Fn}, действующих на фигуру, dΑ − вектор элементарного перемещения точки А.
Второе слагаемое в правой части может быть записано так
(R , dА ) = Rx dxА +Ry dyА .
Подставляя в (200), получим
dA = Mz dφ + Rx dxА +Ry dyА .
Так как q1 = xА , q2 = yА , q3 = φ, то
185
n |
n |
|
Q1 = Rx = ∑npx Fk , Q2 = Ry = ∑npy Fk , |
|
|
k=1 |
k=1 |
(201) |
|
|
|
n
Q3 = M z = ∑mz (Fk ).
k=1
§12. Условия равновесия в обобщенных силах
Теорема. Для того чтобы механическая система, подчиненная идеальным, стационарным, геометрическим, удерживающим связям, находилась в равновесии, необходимо и достаточно, чтобы все обобщенные силы равнялись нулю:
Qi = 0 (I = 1,2,…,s). |
(202) |
Доказательство. В соответствии с принципом возможных перемещений, необходимым и достаточным условием равновесия механической системы, подчиненной идеальным, стационарным, геометрическим, удерживающим связям, является равенство
n |
|
δA = ∑(Fk , δrk ) = 0 , |
|
k=1 |
|
которое согласно формуле (199) может быть записано так |
|
s |
|
δA = ∑Qi δqi = 0. |
(203) |
i=1
Здесь δqi − элементарное (бесконечно малое) приращение обобщенной координаты qi . Заметим, что каждое такое приращение придает системе возможное перемещение, так как оно соответствует наложенным связям.
Пусть система находится в равновесии. Придадим системе возможное перемещение, при котором δq1 ≠ 0, остальные δqi = 0 (I = 2,3,…,s). Тогда из (203) получаем
Q1 = 0.
Придадим теперь системе возможное перемещение, при котором δq2 ≠ 0, остальные δqi = 0 (I = 1,3,…,s). Из (203) находим
Q2 = 0.
186
Продолжая так же действовать и далее, получим
Qi = 0 (I = 3,4,…,s).
Таким образом, из равновесия системы следует (202). Допустим теперь, что выполнены равенства (202). Тогда из (203)
следует, что каковы бы ни были δqi (I = 1,2,…,s), т.е. каково бы ни было возможное перемещение системы δА = 0, а значит, система находится в равновесии. Таким образом, из выполнения равенства (202) следует равновесие системы.
Теорема доказана.
|
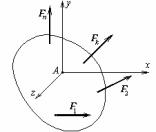
Пример. В качестве примера выведем |
||
|
условия равновесия плоской системы |
||
|
сил. Плоская фигура находится под |
||
|
действием системы сил {F1 , F2 , …, Fn}, |
||
|
лежащей в плоскости фигуры. Проведем |
||
|
оси х и у в этой плоскости, а ось z |
||
|
перпендикулярно ей. Как |
показано в |
|
|
предыдущем |
параграфе, |
обобщенными |
|
силами являются следующие величины |
||
Рис.60 |
|
|
|
|
n |
|
|
Q1 = Rx = ∑npx Fk , |
|
||
|
k=1 |
|
|
|
n |
|
|
Q2 = Ry = ∑npy Fk , |
|
||
|
k=1 |
|
|
|
n |
|
|
Q3 = M z = ∑mz (Fk ), |
|
||
|
k=1 |
|
|
приравнивая которые нулю, получаем уравнения равновесия |
|||
n |
n |
n |
|
∑npx Fk = 0, |
∑npy Fk = 0, |
∑mz (Fk ) = 0, |
|
k=1 |
k=1 |
k=1 |
|
совпадающие с известными уравнениями статики для плоской системы сил.
187
§13. Уравнения Лагранжа
Как отмечалось в §6 настоящей главы добавление сил инерции Jk (k = 1,2,…,n) к силам Fk (k = 1,2,…,n) , действующим на точки механической системы, приводит к расширенной системе сил, удовлетворяющей условиям равновесия. Очевидно, обобщенные силы
Qip (I = 1,2,…,s) расширенной системы сил удовлетворяют равенствам
Qip = Qi + Qiu ,
где Qi − обобщенные силы сил Fk (k = 1,2,…,n) , а Qiu − обобщенные
силы инерции, которые могут быть найдены преобразованием, аналогичным приведенному в §11:
|
n |
∂rk |
|
|
|
u |
= ∑(Jk , |
) (I = 1,2,…,s). |
|
||
Qi |
|
|
(204) |
||
∂q |
i |
||||
|
k=1 |
|
|
|
|
Если связи, наложенные на систему, являются идеальными, стационарными, геометрическими и удерживающими, то согласно предыдущему параграфу при движении системы должны выполняться следующие равенства:
Q |
i |
+ Qu = 0 (I = 1,2,…,s). |
(205) |
|
i |
|
Силы инерции точек механической системы определяются равенствами
|
|
|
|
|
J |
|
= −m |
|
a |
|
= −m |
|
|
dVk |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
k |
k |
k |
k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставив их в (204), будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
dVk |
|
|
∂rk |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
− Qiu |
= ∑mk |
( |
|
, |
) . |
|
|
|
|
|
|
|
(206) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
dt |
|
|
∂qi |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Нетрудно убедиться в том, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
( |
dVk |
, |
∂rk |
) = |
d |
|
(V |
|
, |
|
∂rk |
) − |
(V |
|
|
, |
d |
( |
∂rk |
)) . |
(207) |
||||||||||||||||||
|
|
|
|
k |
|
|
k |
|
|
||||||||||||||||||||||||||||||
|
|
dt |
∂q |
i |
|
dt |
|
|
|
|
|
∂q |
i |
|
|
|
|
|
|
|
|
dt |
|
∂q |
i |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пользуясь правилом Лопиталя, находим |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
∂r |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
r& |
|
|
|
|
∂r& |
|
|
∂V |
k |
|
|
||||||||
|
|
k |
= |
lim |
|
k |
|
= |
|
lim |
|
|
|
|
k |
|
= |
|
|
|
k |
= |
|
|
|
. |
(208) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
∂qi |
|
q |
→0 |
|
qi |
|
|
|
|
q |
|
→0 |
|
|
& |
|
|
|
|
& |
|
|
|
& |
|
|
|
|||||||||||
|
|
i |
|
|
|
|
|
|
|
& |
i |
|
|
|
qi |
|
|
|
|
∂qi |
|
|
∂qi |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что в результате перестановки порядка дифференцирования можно получить следующее равенство
188
d |
( |
∂rk |
) = |
∂ |
( |
drk |
) = |
∂Vk |
. |
(209) |
|
|
|
|
|
||||||
dt |
∂qi |
∂qi dt |
∂qi |
|
||||||
Подставив (208) и (209) в (207), получаем
( |
dVk |
, |
∂rk |
) = |
d |
(V |
|
, |
∂Vk |
) − (V |
|
, |
∂Vk |
) . |
(210) |
|
|
|
k |
|
k |
|
|||||||||
|
dt ∂qi |
dt |
|
& |
|
|
∂qi |
|
|
||||||
|
|
|
∂qi |
|
|
|
|
|
|||||||
Заметим попутно, что q&i (I = 1,2,…,s) носят название обобщенных скоростей.
Дифференцирование квадрата скорости Vk по qi и q&i дает
|
|
|
|
∂V |
2 |
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂V |
k |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
k |
= |
|
|
|
|
|
|
(V |
|
,V |
|
) |
= 2(V |
|
, |
|
|
|
), |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
∂q |
|
|
k |
k |
k |
∂q |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
∂q |
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
∂V |
2 |
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂V |
k |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
k |
= |
|
|
|
|
|
|
(V |
|
,V |
|
) |
= 2(V |
|
, |
|
|
|
). |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
k |
k |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
& |
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
∂qi |
|
|
∂qi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂qi |
|
|
|
|
|
|
|
|
||||||||||||
В результате подстановки их в (210) будем иметь |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
dV |
k |
|
|
∂r |
k |
|
|
|
|
|
d |
|
1 ∂V 2 |
|
|
|
1 ∂V 2 |
|
|
|
|
|||||||||||||||||
|
|
|
( |
|
|
|
, |
|
|
|
) = |
|
|
|
( |
|
|
|
k |
|
) |
− |
|
|
|
|
|
|
k |
. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ∂qi |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
dt ∂qi |
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dt 2 ∂qi |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Остается подставить это выражение в (206): |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂ |
|
n |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
∂ |
|
n |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
∂T |
|
∂T |
|
||||
− Qiu = |
d |
( |
|
|
∑ |
mkVk |
) − |
|
|
|
∑ |
mkVk |
= |
|
d |
( |
|
) − |
. (211) |
|||||||||||||||||||||||||
|
|
& |
|
|
|
|
|
|
|
|
& |
|
||||||||||||||||||||||||||||||||
|
dt |
∂qi k=1 |
|
|
2 |
|
|
|
|
|
|
|
∂qi k=1 |
|
2 |
|
|
|
|
|
|
|
dt |
∂qi |
∂qi |
|||||||||||||||||||
(Т – кинетическая энергия механической системы).
Сучетом (211) равенства (205) принимают следующий вид:
d |
( |
∂T |
) − |
∂T |
= Q |
|
(I = 1,2,…,s). |
(212) |
|
|
|
i |
|||||
dt |
& |
|
∂qi |
|
|
|||
∂qi |
|
|
|
|||||
Эти уравнения представляют собой дифференциальные уравнения
движения механической системы в обобщенных координатах или уравнения Лагранжа.
§14. Пример решения задачи с применением уравнений Лагранжа
Задача. Механическая система (рис.61) состоит из двух грузов 1 и 2 одинаковой массы т1 и трех блоков 3,4 и 5 одинаковой массы т2 и радиуса r, один из которых подвижный, а остальные неподвижные.
189
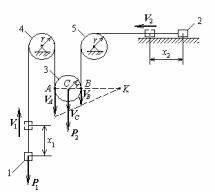
Через блоки переброшена веревка так, как показано на рисунке. К одному концу ее прикреплен груз 1, а к другому − груз 2. Найти ускорения грузов , пренебрегая весом веревки и трением на осях. Система начинает движение из состояния покоя.
Решение. Рассматриваемая механическая система имеет две степени свободы. Выберем в качестве обобщенных координат смещения х1 и х2 грузов 1 и 2 из начального положения. Тогда уравнения Лагранжа будут иметь вид
d |
( |
∂T |
) − |
|
∂T |
|
= Q |
, |
|
|
|
|
|
|
|
||||||
dt |
& |
|
|
1 |
|
|
||||
∂x1 |
∂x1 |
|
(213) |
|||||||
d |
|
∂T |
|
|
∂T |
|
|
|||
( |
) − |
|
= Q |
|
. |
|||||
|
|
|
2 |
|||||||
dt |
& |
|
|
|
∂x2 |
|
||||
∂x2 |
|
|
|
|||||||
Найдем обобщенные силы Qj (j =1,2). Придаем сначала механической системе возможное перемещение, при котором х1 получает приращение δх1, т.е. груз 1 перемещается вверх на δх1, а х2 остается неизменным,
Рис.61 т.е. груз 2 остается на месте. При этом точка А подвижного
блока перемещается вниз на δх1 , а точка В остается на месте. Поэтому точка С перемещается вниз на δх1 / 2 . Работа активных сил на этом перемещении равна
δA1 = − Р1 δх1 |
+ |
P2δx1 |
= ( |
m2 |
− m )gδx . |
|||
|
|
|
||||||
|
2 |
2 |
1 |
1 |
||||
|
|
|
||||||
Поэтому |
|
|
|
|
|
|
|
|
Q1 |
= ( |
m2 |
− m )g . |
|
(214) |
|||
|
|
|||||||
|
2 |
1 |
|
|
|
|||
|
|
|
|
|
|
|||
Придаем теперь системе другое перемещение, при котором х1 остается неизменным (т.е. груз 1 остается на месте), а х2 получает приращение δх2 , т.е. груз 2 перемещается влево на δх2 . При этом точка В подвижного блока перемещается вниз на δх2 , а точка А остается на месте. Поэтому точка С перемещается вниз на δх2 / 2 . Работа активных сил на этом перемещении равна
δA2 |
= |
P2δx2 |
= |
m2 |
gδx |
2 . |
|
|
|||||
|
2 |
2 |
|
|
||
190
