
Курс теоретической механики 2007 (Рус)
.pdf
Пример. Движение материальной точки по поверхности Земли.
В качестве примера изучения относительного движения точки рассмотрим ее движение по поверхности Земли (рис.16). Пусть точка движется в северном полушарии в меридиональном направлении с юга на север. Легко убедиться, используя правило Жуковского построения кориолисова ускорения, что кориолисова сила инерции будет иметь направление, указанное на чертеже, т.е. вправо по отношению к
|
направлению |
движения точки. |
При |
|||
|
движении в других направлениях в |
|||||
|
северном полушарии кориолисова сила |
|||||
|
инерции |
имеет |
|
составляющую, |
||
|
направленную |
таким |
образом. |
Это |
||
|
означает, что при движении точки по |
|||||
|
земной |
поверхности |
в северном |
|||
|
полушарии она отклоняется вправо |
|||||
|
по отношению |
к |
направлению |
|||
|
движения. Этим объясняется то, что в |
|||||
|
северном полушарии реки подмывают |
|||||
|
правый берег, и поэтому он круче лево- |
|||||
Рис.16 |
го (закон Бэра). |
|
|
|
||
|
В |
южном |
полушарии |
точка |
||
отклоняется влево от направления движения |
и |
в соответствии с |
||||
этим реки подмывают левый берег. Поэтому он круче правого. |
|
|||||
.
131

Г Л А В А II
ДИНАМИКА МЕХАНИЧЕСКОЙ СИСТЕМЫ И ТВЕРДОГО ТЕЛА
§1. Механическая система. Внешние и внутренние силы
Механической системой называется совокупность материальных точек, взаимодействующих друг с другом.
Классическим примером механической системы является Солнечная система, в которой все тела взаимодействуют друг с другом посредством сил взаимного гравитационного притяжения.
Твердое тело также представляет собой механическую систему, состоящую из частиц, образующих тело.
Силы, действующие на точки механической системы, делятся на две категории:
1)внешние силы,
2)внутренние силы.
Внешними называются силы, источниками которых являются материальные точки, не принадлежащие данной механической системе.
Внутренними называются силы взаимодействия между точками данной механической системы.
Внешние силы будут обозначаться символом Fe, внутренние – символом Fi.
Свойства внутренних сил.
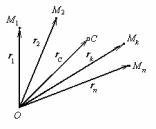
1) Главный вектор внутренних сил равен нулю.
Рассмотрим две какие-либо точки механической системы Мk и Мп (рис.17). По четвертому закону Ньютона они взаимодействуют при помощи двух прямопротивоположных сил
Рис.17 Fki и Fni , геометрическая сумма ко-
торых равна нулю. Поскольку внутренние силы состоят из таких попарно прямопротивоположных сил, то их главный вектор (т.е. общая геометрическая сумма) равен нулю.
132
2) Главный момент внутренних сил относительно любого полюса равен нулю.
Доказывается аналогично.
§2. Центр масс механической системы. Теорема о движении центра масс
Массой механической системы называется сумма масс точек, образующих эту систему:
n
M = ∑mk .
k=1
Центром масс механической системы называется геометрическая точка, радиус-вектор которой определяется по формуле
|
|
n |
|
|
|
|
|
∑mk rk |
|
|
|
r |
= |
k=1 |
. |
|
(74) |
|
|
||||
c |
M |
|
|
|
|
|
|
|
|
|
|
|
|
Здесь mk – массы точек системы (k |
|||
|
=1,2,…,n), rk – их радиус-векторы |
||||
|
(рис.16), М – масса механической |
||||
|
системы. |
|
|
|
|
|
|
Если |
|
спроектировать |
векторное |
|
равенство (74) на оси координат, то |
||||
|
получатся |
|
следующие формулы для |
||
|
координат центра масс |
|
|||
Рис.18
|
|
n |
|
|
n |
|
|
n |
|
|
|
|
∑mk xk |
|
|
∑mk yk |
|
|
∑mk zk |
|
|
xc |
= |
k=1 |
, yc |
= |
k=1 |
, zc |
= |
k=1 |
(75) |
|
M |
M |
M |
||||||||
|
|
|
|
|
|
|
(здесь xk ,yk ,zk - координаты точки Mk ).
Умножим числители и знаменатели формул (75) на ускорение свободного падения тел g. В результате будем иметь
133

|
|
|
n |
|
|
|
n |
|
|
|
n |
|
|
|
|
|
∑Pk xk |
|
|
|
∑Pk yk |
|
|
|
∑Pk zk |
|
|
x |
c |
= |
k=1 |
, y |
c |
= |
k=1 |
, z |
c |
= |
k=1 |
. |
|
P |
P |
P |
|||||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Нетрудно убедиться в том, что это формулы для координат центра тяжести механической системы, находящейся в однородном поле сил тяжести (см. §3 главы IV раздела «Статика»).
Таким образом, если механическая система находится в
однородном поле сил тяжести, то ее центр масс совпадает с центром тяжести
Теорема о движении центра масс. Центр масс механической системы движется как некоторая материальная точка, масса которой равна массе механической системы и на которую действуют внешние силы, приложенные к точкам механической
системы.
Доказательство. Запишем равенство (74) в следующем виде
n
Mrc = ∑mk rk ,
k=1
ипродифференцируем левую и правую части ее по времени дважды
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
&& |
&& |
|
|
|
|
|
|
|
|
|
|
|
Mrc |
= ∑mk rk . |
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
Так как |
&& |
= a , то в результате будем иметь |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
Mac |
= ∑mk ak . |
|
|
|
|
|
|
|
|
(76) |
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
|
|
|
|
aс |
|
− |
ускорение |
|
|
|
|
центра |
масс, |
ak |
|
− ускорение |
|||||
|
|
|
точки |
Mk |
|
(k = 1,2,… ,n). |
||||||
|
|
|
Из третьего закона динамики |
|||||||||
|
|
|
следует (рис.19), что |
|
||||||||
|
|
|
|
m |
k |
a |
k |
= F e |
+ F i . |
|||
|
|
|
|
|
|
|
k |
|
k |
|||
|
|
|
Подставив это в равенство (76), |
|||||||||
|
|
|
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ma |
c |
= Re |
+ Ri , |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
Рис.19 |
где Re = ∑Fke , |
Ri |
= ∑Fki . |
|||||||
|
|
|
|
r=1 |
|
|
|
|
r=1 |
|||
134
Но по свойству внутренних сил
Ri = 0,
и получаем окончательно
Maс = Re , т.е. |
(77) |
произведение массы системы на ускорение ее центра масс равно главному вектору внешних сил.
Возьмем теперь материальную точку Мо с массой, равной массе механической механической системы, и приложим к ней внешние силы, действующие на точки механической системы (рис.20).
Составив для этой точки основное уравнение динамики, получим
Ma = Re.
(а – ускорение упомянутой выше точки). Сопоставив это с (77), приходим к выводу, что ас = а, откуда и следует формулировка теоремы о движении центра масс.
Рис.20
Следствия.
1)Внутренние силы не влияют на движение центра масс.
2)Если главный вектор внешних сил равен нулю в течение
некоторого промежутка времени, то центр масс системы движется равномерно и прямолинейно либо находится в
состоянии покоя в течение этого промежутка.
Доказательство. Из равенства Re = 0 следует aC = 0. Последнее
может быть записано так dVc = 0 , откуда вытекает, что Vс = const. dt
Неизменность направления скорости центра масс означает его движение по прямой, а неизменность ее величины – равномерность этого движения.
§3. Пример решения задачи с применением теоремы о движении центра масс
135
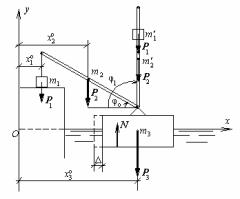
Задача. Понтонный кран поднимает груз массой m1 = 1000кг. Угол наклона стрелы, перемещающейся в вертикальной плоскости, изменяется от φο = 30о до φ1 = 90о (рис.21). Считая стрелу однородным прямолинейным стержнем длиной l = 10 м и массой m2 = 1000 кг, определить перемещение понтона массой m3 = 25000 кг, если в начальный момент кран находился в покое. Сопротивлением воды пренебречь.
Решение. Рассматриваем механическую систему, состоящую из понтонного крана, стрелы и груза. На эту механическую систему действуют следующие внешние силы: вес груза Р1 , вес стрелы Р2 , вес крана Р3 и выталкивающая сила воды N. Все эти силы вертикальны.
На основании теоремы о движении центра масс можем записать
Maс = Re, |
(78) |
где М – масса системы, aс – ускорение центра масс, Re – главный вектор внешних сил:
Re = Р1 + Р2 + Р3 + N . |
(79) |
Проектируем векторное равенство (78) (с учетом (79)) на ось х:
M&x&c = 0 .
Так как масса механической системы не равна нулю, то отсюда следует, что
&x&c = 0 .
Умножим это равенство на dt и проинтегрируем по t. В результате получим
& |
= C1 . |
(80) |
xc |
В начальный момент система находилась в покое.
Рис.21 Поэтому скорость ее центра масс, а значит и ее проекция на ось х (т.е. левая часть (80)) равнялись нулю. Отсюда
следует, что С1 = 0. Таким образом, получаем
136
& |
= 0 . |
(81) |
xc |
Умножаем теперь (81) на dt и интегрируем:
хс = С2, |
(82) |
т.е. абсцисса центра масс механической системы остается неизменной. Найдем абсциссу центра масс в начальный момент (см. рис.21)
|
|
|
m x0 |
+ m |
x0 |
+ m |
x0 |
|
|
x |
|
= |
1 1 |
2 |
2 |
3 |
3 |
. |
(83) |
c |
m1 + m2 + m3 |
|
|||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
Предположим теперь, что в результате перемещения грузов кран
сместился влево на расстояние |
. Новая абсцисса массы m3 будет |
|||
|
x/ |
= x0 − |
, |
|
|
3 |
3 |
|
|
новая абсцисса массы m1 будет |
|
|
|
|
x/ |
= x0 |
+ l cos φ |
0 |
− , |
1 |
1 |
|
|
|
так как в результате поворота стрелы, занявшей вертикальное положение, масса m1 перемещается на расстояние l cos φ0. Аналогично, новая абсцисса массы m2 будет
|
|
|
|
|
|
x |
/ |
= x0 |
+ |
l |
cos φ |
|
− . |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Таким образом, абсцисса центр масс в конечном положении такова |
|||||||||||||||||||||||
|
|
|
m (x0 |
+ l cos φ |
|
− |
) + m |
|
(x0 |
+ |
l |
cos φ |
|
− |
) + m |
|
(x |
0 |
− |
) |
|
||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
/ |
= |
1 1 |
|
0 |
|
|
|
2 |
2 |
2 |
|
|
|
0 |
|
|
3 |
|
3 |
|
|
. (84) |
||
c |
|
|
|
|
|
m1 |
+ m2 + m3 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Поскольку абсцисса центра масс остается неизменной, то правые части (83) и (84) должны быть равны. Таким образом получаем уравнение относительно Δ:
m (l cos φ |
|
− |
) + m |
|
( |
l |
cos φ |
|
− ) − m |
|
= 0 , |
|||
|
|
|
|
|
||||||||||
1 |
0 |
|
|
2 |
2 |
|
|
0 |
|
|
|
3 |
|
|
решая которое, находим |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(m + |
m2 |
)l cos φ |
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|||||||
|
|
= |
1 |
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
. |
|
(85) |
|||
|
|
m1 + m2 + m3 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
Подстановка числовых значений дает следующий результат = 0,48 м.
137
§4. Теорема об изменении количества движения механической системы
Количеством движения материальной точки называется вектор, равный произведению массы точки на ее скорость:
q = mV. (86)
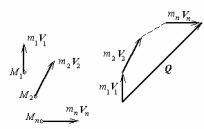
Количеством движения механической системы называется свободный вектор, равный геометрической сумме количеств движения точек системы (рис.22):
n |
|
Q = ∑mkVk . |
(87) |
k=1
Количество движения механической системы равно произведению массы М системы на
скорость Vc ее центра масс:
|
Q = MVc . |
(88) |
|||
|
Доказательство. |
|
Запишем |
||
|
формулу (74) для радиус-вектора |
||||
Рис.22 |
центра масс механической сис- |
||||
|
темы в следующем виде: |
||||
|
n |
|
|
|
|
Mrc |
= ∑mk rk |
|
|
|
|
|
k=1 |
|
|
|
|
и продифференцируем по |
времени. Пользуясь тем, |
что |
|
dr |
=V , |
|
|
||||
|
|
|
|
dt |
|
получим |
|
|
|
|
|
|
n |
|
|
|
|
MVc = ∑mkVk . |
|
(89) |
|||
|
k=1 |
|
|
|
|
Величина, стоящая в правой части (89), в соответствии |
(87) и есть |
||||
количество движения системы Q. Таким образом, получаем |
|
|
|
||
|
Q = MVc , |
|
|
|
|
что и требовалось. |
|
|
|
|
|
Теорема (об изменении количества движения механической системы). Геометрическая производная количества движения
138
механической системы по времени равна главному вектору внешних сил, действующих на точки механической системы, т.е.
(90)
Доказательство. Продифференцируем (88) по времени. Так как
dV = a , то в результате будем иметь dt
dQ |
= Mac , |
(91) |
|
||
dt |
|
|
но по теореме о движении центра масс Mac = Re и (91) запишется так:
dQ = Re , что и требовалось доказать. dt
Следствия.
1)Внутренние силы не влияют на изменение количества движения механической системы.
2)(закон сохранения количества движения) Если главный вектор внешних сил равен нулю в течение некоторого
промежутка времени, то количество движения механической системы не изменяется ни по величине, ни по направлению в течение этого промежутка.
Доказательство. Если Re = 0, то из теоремы следует, что dQ = 0 , dt
азначит, Q = const.
3)(закон сохранения проекции количества движения) Если сумма проекций всех внешних сил на какую-либо ось равна нулю в
течение некоторого промежутка времени, то проекция количества движения на эту ось не изменяется в течение этого промежутка.
Доказательство. Спроектируем равенство (90) на ось х. Так как операции проектирования и дифференцирования перестановочны (§1 главы I раздела II), то в результате получим
dQx |
= Rxe . |
(92) |
|
||
dt |
|
|
139
n |
n |
Но так как Re = ∑Fke , то Rxe = ∑прx Fke , что равно нулю по усло- |
|
k=1 |
k=1 |
вию. Из (92) получаем
dQx = 0 , dt
откуда и вытекает, что Qx = const.
§5. Пример решения задачи с применением теоремы об изменении количества движения механической системы
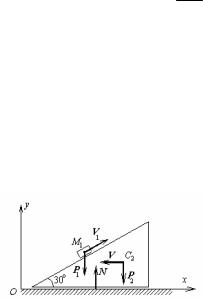
Задача. Треугольная призма массой m2 = 5 кг располагается на гладкой горизонтальной поверхности (рис.23). Вдоль ее наклонной грани движется груз массой m1 = 1 кг с относительной скоростью V1 = 2 м/с. Определить скорость V призмы, если в начальный момент
призма и груз на ней находились в состоянии покоя.
Решение. Будем полагать, что механическая система состоит из двух тел: призмы и груза. Тогда внешними по отношению к ней являются следующие силы: вес груза Р1 и вес призмы Р2, а также нормальная реакция поверхности
Рис.23 N, на которой располагается призма. Все эти силы вертикальны. Поэтому их проекции на горизонтальную ось х равны нулю. Тогда
на основании закона сохранения проекции количества движения (см. предыдущий параграф) мы можем записать
Qx = const.
В начальный момент система находилась в покое, поэтому мы можем сделать вывод, что
Qx = 0 |
(93) |
в любой момент времени.
Рассмотрим движение груза как сложное: его движение относительно призмы будем считать относительным, а движение призмы переносным. Тогда абсолютная скорость груза будет равна
140
