
Курс теоретической механики 2007 (Рус)
.pdf
δст = |
P |
. |
(44) |
|
|||
|
c |
|
|
Найдем теперь геометрическую сумму сил, действующих на точку в произвольном положении:
F1 = F + P = −c OM + P . Подставив сюда Р из (42), будем иметь
F1 = −c OM + c OO1 = −c O1M .
Это означает, что фактически точка движется под действием силы F1 , которая является восстанавливающей, центр которой находится в новом положении равновесия О1 , смещенном на расстояние δст от старого положения равновесия. Отсюда вытекает справедливость всех выводов предыдущего параграфа и в этом случае. Таким образом,
добавление постоянной силы не изменяет характера свободных колебаний – они остаются гармоническими, но центр колебаний смещается на величину статического смещения в сторону действия постоянной силы.
Из (33) и (44) имеем
|
k 2 = |
|
P |
. |
|
||||
|
|
|
|
|
|||||
|
|
|
mδст |
|
|
||||
Тогда |
|
|
|
|
|
|
|||
|
2π |
|
|
|
|
|
|
||
T = |
= 2π |
|
m |
δ |
|
. |
|||
|
|
ст |
|||||||
|
k |
|
P |
|
|||||
|
|
|
|
||||||
Это означает, что период колебаний пропорционален корню
квадратному из статического смещения.
Если сила Р является силой тяжести, т.е. когда колебания
происходят по вертикальной прямой, то P = mg и |
|
T = 2π δст . |
(45) |
g
§7. Свободные колебания материальной точки при наличии вязкого сопротивления
Пусть теперь помимо восстанавливающей силы F на материальную точку действует сила сопротивления R, пропорциональная первой степени скорости точки, т.е.
121

R = − bV. |
(46) |
Знак минус в равенстве (46) означает, что сила сопротивления направлена противоположно скорости. Составим основное уравнение динамики
Рис.9
ma = F + R
и спроектируем его на ось х:
&& |
& |
(47) |
mx |
= −cx − bx . |
Разделим (47) на m и в результате получим дифференциальное
уравнение свободных колебаний материальной точки при наличии вязкого сопротивления
&& |
& |
2 |
x = 0 . |
(48) |
x |
+ 2βx + k |
|
Здесь β = b / 2m. Уравнение (48) – это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Составим характеристическое уравнение:
λ2 + 2βλ + k2 = 0. |
(49) |
Его корни имеют следующий вид:
λ1,2 = − β ± β2 − k 2 . |
(50) |
1. Рассмотрим сначала случай малого сопротивления β < k.
Введем обозначение
k1 = k 2 −β2 . |
(51) |
Тогда корни характеристического уравнения запишутся так:
λ1,2 = − β ± ik1 ,
т.е. корни характеристического уравнения являются комплексными. Общее решение дифференциального уравнения (49) в этом случае
записывается так:
x = e− βt (C1 sin k1 t + C2 cos k1t).
Произведя внутри скобок преобразования аналогично §5, получим
122
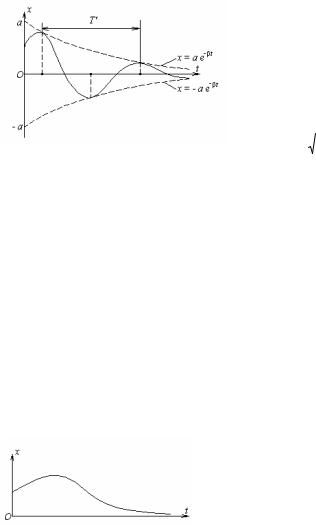
x = a e− βt sin (k1t + α), |
(52) |
причем величины а и α определяются из начальных условий.
Колебания, происходящие по закону x = a e− βt sin (k1t + α), называются затухающими, так как величина e− βt стремится к нулю с течением времени. График функции (52) представлен на рис.10. Период функции sin (k1t + α) будем называть периодом затуха-
ющих колебаний:
|
T' = |
2π |
= |
|
2π |
|
|
. (53) |
|
|
|
|
|
|
|||
|
|
k1 |
|
k 2 −β2 |
||||
Рис.10 |
Сравнивая с (36), приходим |
|||||||
|
к выводу, |
что Т’ > Т, т.е. |
||||||
при наличии сопротивления период |
колебаний увеличивается. |
|||||||
Формула (52) показывает, что за один период размах |
колебаний |
|||||||
уменьшается в e−βT ' раз. |
|
|
|
|
|
|
|
|
e−βT '
Величина называется декрементом затухающих колебаний, а величина βT’ − логарифмическим декрементом.
2.Граничный случай β = k.
Вэтом случае корни характеристического уравнения (49) вещественны и равны друг другу:
λ1 = λ2 = − β. |
|
|
Общее решение уравнения (48) имеет вид |
|
|
х = е− βt (C1 + C2 t). |
|
(54) |
Нетрудно |
проверить, |
что из |
начальных условий |
|
|
& |
при t = 0 |
(55) |
х = хо , x =Vo |
||
|
следует, что C1 = хо , C2 = Vo +βхо . |
|
Тогда уравнение движения точки |
Рис.11 |
будет выглядеть так: |
123

х = е− βt [xo + (Vo +βхо) t]. |
(56) |
График функции (56) при хо > 0 и Vo > 0 представлен на рис. 11. Из графика видно, что движение точки в этом случае вообще
не носит колебательного характера, т.е. оно является апериодическим.
Легко проверить, что оно является таковым и при других значениях
хо и Vo .
3.Случай большого сопротивления β > k.
Вэтом случае оба корня являются вещественными и отрицательными
λ1 = − β + 
 β2 − k 2 , λ2 = − β −
β2 − k 2 , λ2 = − β − 
 β2 − k 2 .
β2 − k 2 .
Общее решение дифференциального уравнения (49) представляется в следующем виде:
х = C1 exp (λ1 t) + C2 exp (λ2 t).
Определив значения постоянных интегрирования из начальных условий (55), получаем уравнения движения точки
х = |
λ2 xo −Vo |
exp (λ1 t) + |
Vo |
− λ1xo |
exp (λ2 t). |
||
λ2 |
− λ1 |
λ2 − λ1 |
|||||
|
|
|
|||||
График этой функции имеет вид, представленный на рис.11, т.е. и
в этом случае движение является апериодическим.
§8. Вынужденные колебания материальной точки. Резонанс
Пусть теперь на материальную точку действуют две силы: F - восстанавливающая и Q – периодически зависящая от времени
Q = Qo sin pt |
(57) |
( Qo − постоянная сила, направленная вдоль оси х в положительном ее направлении).
Сила Q = Qo sin pt называется возмущающей силой, а колебания
под действием такой силы называются вынужденными.
Дифференциальное уравнение движения точки в этом случае выглядит так
m&x& = −cx + Q |
o |
sin pt . |
(58) |
|
|
|
124

Разделим обе части (58) на m
&x&+ k 2 x = P sin pt |
(59) |
o |
|
(здесь Ро = Qo / m ).
Это дифференциальное уравнение вынужденных колебаний материальной точки при отсутствии сил сопротивления.
Как известно из теории дифференциальных уравнений общее решение его представляется в следующем виде:
х = х1 + х2 ,
где х1 − общее решение однородного уравнения (т.е. уравнения (59) с правой частью, равной нулю), а х2 − какое либо частное решение уравнения (59). Рассмотрим два случая.
1. Нерезонансный случай р ≠ k (частота вынуждающей силы
не равна частоте свободных колебаний).
В этом случае частное решение х2 ищется в следующем виде
x2 = A sin pt, |
(60) |
где А − искомая постоянная величина.
Подставим выражение (60) в дифференциальное уравнение (59):
− p2 A sin pt +k2 A sin pt = Po sin pt.
Это равенство должно выполняться при любом значении t, поэтому A (k2 − p2) = Po , т.е.
А = |
Po |
|
|
. |
|
k 2 − p2 |
||
Таким образом, частное решение выглядит так
Po |
|
|
х2 = k 2 − p2 |
sin pt. |
(61) |
Общее решение однородного уравнения было найдено в §5
х1 = a sin (kt + α). |
(62) |
Следовательно, общее решение уравнения (59) таково
125
х = a sin (kt + α) + |
Po |
sin pt. |
(63) |
k 2 − p2 |
Величины а и α определяются из начальных условий (55).
Формула (63) показывает, что колебания точки под действием
возмущающей силы в нерезонансном случае складываются из собственных колебаний, происходящих с частотой свободных колебаний, и вынужденных колебаний, происходящих с частотой вынуждающей силы.
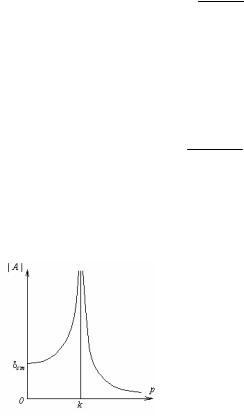
График зависимости амплитуды вынужденных колебаний
| A | = Po
| k 2 − p2 |
от частоты вынуждающей силы представлен на рис.12.
Заметим, что при р = 0 амплитуда | A | = Ро / k2 = Qo / c = δст . С увеличением р при р < k , амплитуда вынужденных колебаний
возрастает и при приближении р к k она стремится к бесконечности, затем при р > k с возрастанием р она стремится к нулю.
Заметим также, что при р < k знаки А и Ро совпадают, т.е. фазы вынужденных колебаний и вынуждающей силы совпадают, а при р > k знак А противоположен знаку Ро , т.е. фазы вынужденных колебаний и вынуждающей силы противоположны. Это значит, что когда вынуждающая сила направлена вправо, точка смещается влево, и наоборот.
Рис.12
2. Резонанс р = k (частота вынуждающей силы равна частоте
свободных колебаний).
В этом случае частное решение х2 уравнения (59) ищется в следующем виде
x2 = At сos pt. |
(64) |
Подставив его в (59), будем иметь |
|
||
A = − |
Po |
, |
(65) |
|
|||
|
2p |
|
|
126
т.е. уравнение вынужденных колебаний выглядит так
x2 = − Po t сos pt.
2p
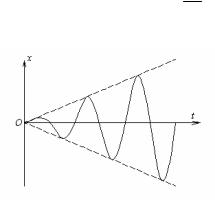
Это значит, что при резонансе с возрастанием t
амплитуда колебаний растет неограниченно по линейному закону, т.е. наблюдается «раскачка» колебаний
(рис.13). В этом и заключается явление резонанса. Поэтому оно считается опасным и во многих отраслях техники его стараются избежать.
Рис.13
§9. Вынужденные колебания материальной точки при наличии сопротивления
Пусть теперь материальная точка движется под действием трех сил: восстанавливающей силы F, определяемой формулой (31), силы сопротивления R (46) и возмущающей силы Q (57). Дифференциальное уравнение движения точки в этом случае
&& |
& |
sin pt . |
(66) |
mx |
= −cx − bx + Qo |
Разделив обе части (66) на m и учитывая принятые в предыдущих параграфах обозначения, получим
&& |
& |
2 |
x = Po |
sin pt . |
(67) |
x |
+ 2βx + k |
|
Это дифференциальное уравнение вынужденных колебаний при наличии сопротивления.
Общее решение его х (как и в предыдущем параграфе) представляется в виде
х = х1 + х2 ,
127
где х1 − общее решение однородного уравнения (т.е. уравнения (67) с правой частью, равной нулю), а х2 − какое либо частное решение уравнения (67). Заметим, что х1 определяют так называемые собственные колебания, х2 – вынужденные колебания.
Вид решения х1 при различных соотношениях параметров β и k приведен в §7, причем там было показано, что собственные колебания, определяемые этим решением, являются затухающими и спустя некоторый промежуток времени практически исчезают, т.е. общее решение для достаточно больших значений t совпадает с х2.
Частное решение х2 будем искать в следующем виде:
х2 = А sin (pt − γ), |
(68) |
где А и γ − постоянные параметры, подлежащие определению. Подставляя (68) в уравнение (67), получим
A(−p2 + k2 ) sin (pt − γ) + 2βp cos (pt − γ) = |
|
= Po [ cos γ sin (pt − γ) + sin γ cos (pt − γ)]. |
(69) |
Для того чтобы равенство (69) выполнялось при любых значениях t необходимо, чтобы коэффициенты при sin (pt − γ) и cos (pt − γ) в левой и правой частях равенства были равны:
A (k2 − p2) = Po cos γ, 2βpA = Po sin γ. |
(70) |
Возводя равенства (70) в квадрат и складывая их, получаем
A = |
|
|
Po |
|
|
|
|
. |
(71) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||||
|
|
(k 2 − p2 )2 + 4β2 p2 |
|
||||||
Разделим второе |
равенство (70) |
||||||||
на первое |
|
|
|
|
|
|
|||
|
|
tg γ = |
|
2βp |
|
. |
|
|
(72) |
|
|
|
|
|
|
|
|||
|
|
|
k 2 − p2 |
|
|||||
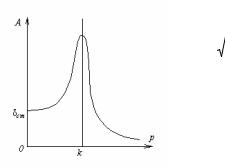
Равенства (71) и (72) определяют амплитуду и фазу вынужденных коРис.14 лебаний. График зависимости амплитуды от частоты возмущающей силы
приведен на рис.14. Как следует из зависимости (71), а также из
128
графика на рис.14, амплитуда А при любом значении р, даже при p = k, принимает конечное значение.
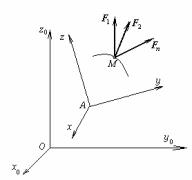
§10. Динамика относительного движения материальной точки
Рассмотрим движение материальной точки М относительно некоторой системы отсчета xyz, которая совершает произвольное движение относительно инерциаль-
|
ной системы отсчета xoyozo (рис.15). |
|||||
|
Очевидно, |
система |
отсчета xyz |
|||
|
вообще |
говоря |
не |
является |
||
|
инерциальной. |
|
|
|
||
|
Движение |
точки |
относительно |
|||
|
инерциальной |
|
системы |
отсчета |
||
|
xoyozo будем считать абсолютным, |
|||||
|
движение ее относительно системы |
|||||
|
отсчета |
xyz |
|
будем |
считать |
|
|
относительным, |
а |
движение |
|||
|
системы xyz относительно xoyozo − |
|||||
Рис.15 |
переносным. |
|
|
|
|
|
|
Составим |
основное |
уравнение |
|||
динамики точки для ее движения относительно инерциальной системы xoyozo
n
maa = ∑Fk .
k=1
По теореме Кориолиса
aa = a + ae +ak,
где через а обозначено ускорение точки относительно системы отсчета xyz. Подставив это в основное уравнение динамики, будем иметь
n
ma = ∑Fk − mae − mak .
k=1
Введем следующие определения.
Переносной силой инерции называется вектор, определяемый по формуле
Je = −mae .
129
Кориолисовой силой инерции называется вектор, определяемый по формуле
Jk = −mak .
С учетом этих определений получаем
n |
|
ma = ∑Fk + Je + Jk . |
(73) |
k=1
Равенство (73) носит название основного уравнения динамики для относительного движения точки. Таким образом, при составлении
основного уравнения динамики относительного движения точки необходимо к действующим на точку силам добавить переносную и кориолисову силы инерции.
Рассмотрим частные случаи.
1) Переносное движение поступательное. В этом случае Jk , так как ak равно нулю, и основное уравнение принимает следующий вид:
n
ma = ∑Fk + Je .
k=1
2)Переносное движение поступательное, равномерное и прямолинейное. В этом случае Jе = Jk = 0 и основное уравнение динамики
принимает такой же вид, как и при движении точки относительно инерциальной системы отсчета
n
ma = ∑Fk .
k=1
Это означает, что система отсчета, движущаяся относительно
инерциальной поступательно, равномерно и прямолинейно сама является инерциальной.
3) Точка неподвижна в подвижной системе координат (находится в состоянии относительного покоя). В этом случае
относительное ускорение а = 0, а также Jk = 0, так как Vr = 0. Основное уравнение принимает вид
n
∑Fk + Je = 0 .
k=1
Таким образом, при определении положения относительного
покоя необходимо ко всем действующим на точку силам добавить переносную силу инерции.
130
