
Курс теоретической механики 2007 (Рус)
.pdf
F = F1 + F2 |
(15) |
Резюмируя вышесказанное, можем сформулировать следующее:
равнодействующая двух параллельных сил, направленных в одну сторону, параллельна силам, направлена в ту же сторону и по величине равна сумме величин сил. Точка приложения равнодействующей на отрезке, соединяющем точки приложения сил, делит этот отрезок в отношении, обратном отношению величин этих сил.
2. Две неравные по величине параллельные силы, направ-
ленные в противоположные стороны. |
|
Повторяя построения предыдущего пункта, получаем |
в этом |
случае, что линия действия равнодействующей проходит за |
преде- |
лами отрезка АВ. Точка С пересечения ее с продолжением отрезка АВ определяется пропорцией
AC |
= |
F2 |
. |
(16) |
|
|
|||
BC F1 |
|
|||
Кроме того, так как F = R = F1 + F2, то в данном случае F = F2 – F1. Итак,
равнодействующая двух неравных по величине параллельных сил, направленных в противоположные стороны, параллельна силам, направлена в сторону большей из них и по модулю равна абсо лютной вели-
Рис.19 чине разности вели-
чин сил. Точка приложения равнодействующей на продолжении отрезка, соединяющего точки приложения сил, делит этот отрезок в отношении, обратном величинам этих сил внешним образом.
3.Пара сил.
Будем рассматривать пару сил как предельный случай предыдущей системы сил, при котором модуль силы F2 стремится к модулю силы
21

F1, т.е в пропорции (16) необходимо сделать предельный переход F2 → F1. Представим ее в следующем виде:
AB + BC = F2
BC F1
и определим из нее длину отрезка ВС:
BC = AB F1 F2 − F1
Если F2 → F1, то F = F2 – F1 → 0, а ВС→ ∞, т.е. точка приложения равнодействующей уходит в бесконечность, а величина ее стремится к нулю. Это означает, что
пара сил равнодействующей не имеет.
§ 18. Отличия равнодействующей от главного вектора
Геометрическое равенство равнодействующей и главного вектора не означает, что эти понятия тождественны. Следует их различать:
1.Главный вектор существует у любой системы сил, а равнодействующая не у любой, как показывает пример 3 предыдущего параграфа.
2.Главный вектор – это свободный вектор, а равнодействующая – скользящий,
т.е. который можно перемещать вдоль линии действия. Действительно, это можно осуществить при помощи элементарных операций.
3.Главный вектор – это понятие геометрическое, а равнодействующая - физическое.
Главный вектор определяется геометрической операцией сложения сил, а равнодействующая находится при помощи элементарных операций, которые имеют определенный физический смысл (см. следующий параграф).
§19. Аксиомы статики
Ваксиомах статики формулируются простейшие условия равновесия тел, законы взаимодействия тел при равновесии, а также приводятся простейшие действия, которые не нарушают равновесия тела. Аксиомы статики являются результатом обобщения огромного количества наблюдений в процессе практической деятельности. Кроме того, результаты теории, построенной на базе этих аксиом, также
22

подверглись многолетней опытной проверке.
Следует отметить, что аксиомы статики являются следствием более общих аксиом, формулируемых в динамике.
Аксиома 1. Для того чтобы тело под действием двух сил находилось в равновесии, необходимо и достаточно, чтобы эти силы были прямопротивоположными.
Рис.20
Аксиома 2 (физическое свойство элементарных операций).
Элементарные операции не нарушают равновесия тела. Следствие 1. Тело не может находиться в равновесии под
действием одной силы.
Доказательство (от противного). Пусть тело находится под действием одной силы F, приложенной в точке А. Предположим, что оно находится в равновесии. Используем первую элементарную операцию: добавим две прямопротивоположные силы Р1 и Р2, причем Р1
|
тоже приложена |
в точке |
А и |
|
|
имеет тоже направление, что и F. |
|||
|
Используем теперь третью элемен- |
|||
|
тарную операцию и заменим две силы |
|||
|
F и Р1 одной силой |
Q = F + P1. В |
||
|
результате |
оказывается, что |
тело |
|
|
находится под действием двух сил Q и |
|||
Рис.21 |
Р2, причем Q = F+P1 > Р2 (так как Р2 = |
|||
|
= Р1), т.е. тело находится в равновесии |
|||
под действием двух сил, которые не являются прямопротивоположными, что противоречит первой аксиоме статики. Таким образом, наше предположение о том, что тело находится в равновесии неверно.
Следствие 2. Перенос силы вдоль ее линии действия из одной точки твердого тела в другую не нарушает равновесия тела.
Такой перенос может быть осуществлен при помощи элементарных операций (§13).
23

Аксиома 3 (равенство действия и противодействия). Два тела взаимодействуют при помощи прямопротивоположных сил
(рис.22).
Аксиома 4 (принцип отвердевания). Равновесие деформируемого тела не нарушится, если оно станет абсолютно твердым.
|
|
Эта |
аксиома |
позволяет |
|
|
|
использовать |
условия |
равновесия |
|
|
|
абсолютно |
твердого |
тела |
при |
|
|
исследовании |
равновесия |
дефор- |
|
|
|
мируемых тел. |
|
|
|
|
|
Тела, на перемещения которых не |
|||
|
|
наложены ограничения, называются |
|||
|
Рис.22 |
свободными. В противном случае |
|||
|
|
тела называются несвободными. |
|||
Тела, |
ограничивающие |
перемещения несвободного |
тела, |
||
называются связями. |
|
|
|
|
|
Реакциями связей называются силы, с которыми связи действуют на несвободное тело.
Аксиома 5 (принцип освобождения от связей). Несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие на тело реакциями этих связей.
§20. Основные типы связей и их реакции.
1.Идеально гладкая поверхность.
|
Идеально гладкой называ- |
|
|
ется поверхность, |
которая |
|
не оказывает сопротивления |
|
|
перемещению тела |
вдоль |
|
поверхности. |
|
|
Реакция идеально гладкой по- |
|
|
верхности направлена по нор- |
|
|
мали к поверхности в точке |
|
Рис.23 |
соприкосновения тела и по- |
|
|
верхности (т.е. перпендику- |
|
лярно касательной плоскости к поверхности).
Это объясняется тем, что в противном случае реакция имела бы
24

составляющую в касательной плоскости, оказывающую сопротивление перемещению тела вдоль поверхности.
2. Связь с неподвижной осью вращения (неподвижный цилиндрический шарнир, подшипник).
Несвободное тело прикреплено к валу подшипника (шарнира). Соприкасающиеся поверхности вала и подшипника предполагаются цилиндрическими и идеально гладкими (рис.24а).
Рис.24
Поэтому реакция неподвижного цилиндрического шарнира
проходит |
через ось шарнира, лежит в плоскости, |
перпендикулярной оси, и раскладывается на две составляющие в этой плоскости (рис.24б).
3. Связь с неподвижным центром вращения (неподвижный сферический шарнир, подпятник).
Сферический шарнир представляет собой шар, находящийся в сферической полости (рис.25а). Такая связь оставляет неподвижным цетр шара, связанного с несвободным телом.
Соприкасающиеся Рис.25 поверхности пред-
полагаются идеально гладкими, поэтому реакция направлена вдоль нормали к сфере, т.е. вдоль ее радиуса, а значит, через центр. Кроме того, так как положение точки соприкосновения поверхностей заранее неизвестно, то неизвес-
25
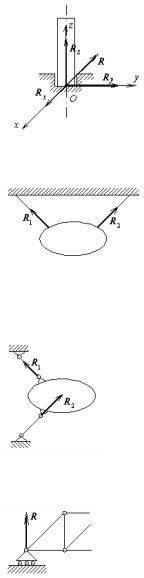
тно и направление реакции. Таким образом, |
|
|
||
|
реакция сферического шарнира проходит |
|||
|
через его центр, может иметь |
|||
|
произвольное |
направление |
в |
|
|
пространстве и поэтому раскладывается |
|||
|
на три составляющие вдоль трех осей |
|||
|
координат (рис.25б). |
|
|
|
|
Три составляющих имеет также реакция |
|||
|
подпятника |
(упорного |
подшипника), |
|
|
препятствующая смещению конца вала в |
|
||
Рис.26 |
любом направлении (рис.26). |
|
|
|
4.Идеально гибкая невесомая нерастяжимая нить.
Реакция нити направлена вдоль нити и внутрь нее, так как отклонение реакции от направления нити означало бы, что нить сопротивляется изгибу, что противоречит ее идеальной гибкости(рис.27).
Рис.27
5.Абсолютно твердый невесомый прямолинейный стержень
с шарнирами на концах.
Реакция стержня направлена вдоль его оси, так как отклонение направления реакции от оси стержня означало бы наличие сил сопротивления в шарнирах, в то время в нем соприкасающиеся поверхности идеально гладкие. При этом реакция может быть направлена как внутрь стержня, так и наружу, в зависимости от того, растянут стержень или сжат (рис.28).
Рис.28
6.Шарнирно-подвижная опора.
Представляет собой комбинацию из двух типов связей: неподвижного цилиндического шарнира и идеально гладкой поверхности, вдоль которой может перемещаться шарнир. Поэтому
реакция шарнирно-подвижной опоры проходит через ось шарнира и направлена перпендикулярно Рис.29 поверхности, вдоль которой опора может пере-
26
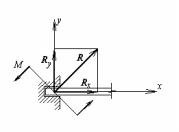
мещаться (рис.29).
7.Жесткая заделка.
|
Так как жесткая заделка препятствует |
|
|
перемещению |
конца несвободной |
|
балки как по горизонтали, так и по |
|
|
вертикали, то |
реакция жесткой |
|
заделки имеет две составляющих: |
|
|
горизонтальную и вертикальную. |
|
|
Кроме того, в жесткой заделке |
|
|
присутствует |
и реактивная пара |
|
сил с неизвестным моментом М, |
|
|
так как жесткая заделка препятствует |
|
Рис.30 |
повороту балки. |
|
27
Г Л А В А II
УСЛОВИЯ РАВНОВЕСИЯ ТЕЛА
§ 1. Основная лемма статики
Любую систему сил при помощи элементарных операций
можно привести к двум силам.
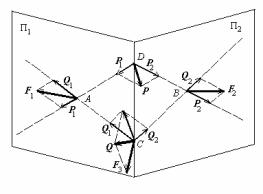
Доказательство. Докажем сначала лемму для того случая, когда
|
исходная |
система |
сил |
||
|
состоит из трех сил F1, |
||||
|
F2, F3, приложенных в |
||||
|
точках А, В и С |
||||
|
(рис.31). Будем пола- |
||||
|
гать |
при |
этом, |
что |
|
|
никакие две |
силы |
из |
||
|
этих трех (в частности, |
||||
|
F1 и F2) не лежат в |
||||
|
одной плоскости, |
по- |
|||
|
скольку иначе доказа- |
||||
|
+тельство |
тривиально. |
|||
|
Проведем |
плоскость |
|||
|
Π1 через линию дейст- |
||||
Рис.31 |
вия силы F1 и точку С. |
||||
|
Затем проведем плос- |
||||
кость Π2 через линию действия силы F2 и точку С. Эти плоскости |
|||||
пересекаются, так как они имеют общую точку С. |
Выберем |
произ- |
|||
вольную точку D (отличную от точки С) |
на линии пересечения |
||||
плоскостей и проведем две прямые в плоскости Π1: одну – через точки А и С, другую – через точки А и D. Эти две прямые задают два направления, проходящих через точку А, вдоль которых мы разложим силу F1 на две составляющие Р1 и Q1. Это можно осуществить при помощи элементарных операций (см. §13 главы I). Затем аналогично проведем в плоскости Π2 две прямые: одну – через точки В и С, другую – через точки В и D. Они задают два направления, проходящие через точку В, вдоль которых разложим силу F2 на две составляющие Р2 и Q2. Перенесем, используя элементарные операции, силы Р1 и Р2 вдоль их линий действия в точку D. Затем применим третью элементарную операцию: заменим силы Р1 и Р2, приложенные в точке
28
D, одной силой Р, приложенной в этой точке. Аналогично, перенесем, силы Q1 и Q2 вдоль их линий действия в точку С и, дважды применив третью элементарную операцию, заменим силы F3, Q1 и Q2, приложенные в точке D, одной силой Q, приложенной в этой точке. В результате остаются только две силы: Р, приложенная в этой точке D, и Q, приложенная в точке С.
Если исходная система состоит из большего, чем три, числа сил, то, выбрав любые три из них, приводим их, используя доказанный частный случай леммы, при помощи элементарных операций к двум силам. Таким образом, число сил в системе уменьшается на единицу. Так продолжаем до тех пор, пока число сил не станет равным двум.
Лемма доказана.
§ 2. Основная теорема статики (геометрические условия равновесия произвольной системы сил)
Для того чтобы тело под действием произвольной системы сил S{F1,F2,…,Fn} находилось в равновесии, необходимо и
достаточно, чтобы главный вектор и главный момент относительно произвольно выбранного полюса этой системы сил
равнялись нулю.
Докажем необходимость условий равновесия (т.е. покажем, что из равновесия тела следует равенство нулю главного вектора и главного момента системы сил, действующих на тело).
Разобьем доказательство на ряд этапов:
1. Используем основную лемму и приводим при помощи элементарных операций систему S{F1,F2,…,Fn} к системе S1{P,Q}, состоящей из двух сил. Как следует из аксиомы 2, равновесие тела при этом не нарушится.
2. Тело оказывается в равновесии под действием двух сил P и Q. Из аксиомы 1 следует, эти силы являются прямопротивоположными.
Тогда
R (S1) =P + Q = 0,
M0 (S1) = m0(P) + m0(Q) = 0
(О – произвольный полюс), причем второе равенство следует из свойства 3 момента силы относительно полюса (§4 главы I).
3.Поскольку системы S1{P,Q} и S{F1,F2,…,Fn} эквивалентны, то
29
R (S) = R (S1) = 0, M0 (S) = M0 (S1) = 0,
(что и требовалось доказать).
Докажем достаточность условий равновесия (т.е. покажем, что из равенства нулю главного вектора R системы сил, действующих на тело, и главного момента ее M0 относительно произвольно выбранного полюса О следует, что тело находится в
равновесии).
Разобьем доказательство на ряд этапов:
1. Используем основную лемму и приводим при помощи элементарных операций систему S{F1,F2,…,Fn} к системе S1{P,Q}, состоящей из двух сил. Как следует из геометрических свойств элементарных операций, главный вектор и главный момент системы сил останутся при этом неизменными, т.е.
R (S1) = R (S) = 0,
M0 (S1) = M0 (S) = 0.
2.Отсюда следует, что
P + Q =R (S1) = 0,
m0(P) + m0(Q) =M0 (S1) = 0.
Такими свойствами обладают только две прямопротивоположные силы, т.е.
S1{P,Q} – п.п.с.
3. Таким образом, тело оказалось под действием двух прямопротивоположных сил. В соответствии с аксиомой 1 оно находится в равновесии. Если осуществить обратный переход от системы S1{P,Q} к системе S{F1,F2,…,Fn} при помощи элементарных операций, то равновесие тела не нарушится, т.е. оно будет находиться в равновесии под действием системы сил S{F1,F2,…,Fn}.
Теорема доказана.
§ 3. Аналитические условия равновесия произвольной системы сил
Для того чтобы тело под действием произвольной системы сил находилось в равновесии, необходимо и достаточно, чтобы
30
