
Курс теоретической механики 2007 (Рус)
.pdf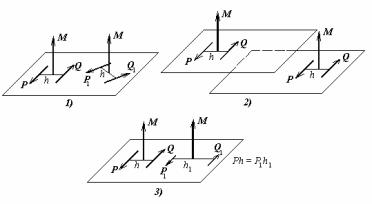
ные силы.
§ 2. Эквивалентные преобразования пар
Из следствия 1 предыдущего параметра вытекает, что любые преобразования одной пары сил в другую, оставляющие ее момент неизменным, приводят к паре, эквивалентной исходной.
Преобразования пар, не изменяющие ее момента, называются эквивалентными.
Приведем некоторые примеры эквивалентных преобразований:
1.перемещение пары в своей плоскости без изменения величины сил, плеча и направления вращения,
2.перенос пары из своей плоскости в параллельную ей плоскость без изменения величины сил, плеча и направления вращения,
3. одновременное изменение величины сил, образующих пару, и ее плеча, при котором остается неизменным произведение величины сил на плечо.
Нетрудно убедиться, что во всех трех случаях не меняется ни направление момента, ни его величина (рис.38).
Рис.38
§ 3. Теорема Пуансо о приведении системы сил к заданному центру
Любая система сил S эквивалентна системе S1{F,P,Q} из трех
сил, первая из которых F геометрически равна главному вектору R
41

системы S и приложена в любой заранее выбранной точкеO
(именуемой центром приведения), а остальные две образуют а) пару сил с моментом М, равным главному моменту Мо
системы S относительно центра приведения О, если этот главный
момент отличен от нуля; б) две прямопротивопложные силы, если главный момент Мо
системы S относительно центра O приведения равен нулю.
Доказательство.
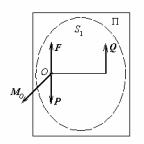
Случай а). Найдем главный вектор системы S1, изображенной на рис.39:
|
R(S1) = F + P + Q = F. |
|
|
Но F = R(S) по условию. Тогда оказыва- |
|
|
ется, что |
|
|
R(S1) = R(S). |
(29) |
|
Аналогично, |
|
Рис.39 |
Mo(S1) = mo(F) + mo(P) +mo(Q) |
|
Но mo(F) = 0, так как сила F приложена прямо в центре приведения О,
а
mo(P) +mo(Q) =М,
который по условию равен Мо(S1). Таким образом, |
|
|
|
Mo(S1) = Mo(S). |
(30) |
Из (29) и (30), а |
также из общего признака эквивалентности |
|
систем сил получаем |
|
|
|
S ~ S1. |
|
Случай б). Очевидно, что и в этом случае |
|
|
|
R(S1) = F + P + Q = R(S), |
(31) |
|
а |
|
|
Mo(S1)=mo(F)+mo(P+mo(Q)=0=Mo(S), (32) |
|
|
так как mo(P) +mo(Q) = 0, поскольку {P,Q} – |
|
Рис.40 |
п.п.с. Из (31), (32) и общего признака эквива- |
|
42
лентности систем сил следует
S ~ S1.
Теорема Пуансо доказана.
§4. Частные случаи теоремы Пуансо
1.R(S) = 0, Mo(S) = 0.
Вэтом случае F = 0, и система S эквивалентна двум
прямопротивоположнным силам S1{P,Q}.
2.R(S) = 0, Mo(S) ≠ 0.
Вэтом случае также F = 0, но из-за того, что Mo(S) ≠ 0, система S
эквивалентна паре сил S1{P,Q}.
3.R(S) ≠ 0, Mo(S) = 0.
Вэтом случае F ≠ 0, но из того, что Mo(S) = 0, следует {P,Q} –
п.п.с. (рис.39). Используя вторую элементарную операцию, удаляем их. В результате получаем
S ~ S1{F},
т.е. система S приводится к одной силе – равнодействующей.
4.R(S) ≠ 0, Mo(S) ≠ 0, R(S) Mo(S).
Так как плоскость пары сил перпендикулярна ее моменту, то в этом случае оказывается, что сила F, равная R(S), параллельна плоскости пары {P,Q}. Путем переноса пары в параллельную плоскость (см. §2) можно добиться того , чтобы F, P и Q оказались в одной плоскости Π. Затем перемещая ее в этой плоскости и меняя величины сил и плечо так, чтобы момент остался неизменным, можно добиться того,
Рис.41 чтобы одна из сил P пары стала прямопротивоположной силе F (рис.41). Используя теперь вторую элементарную операцию, отбросим две
прямопротивоположные силы F и P. В результате в системе S1 останется только одна сила Q, которая и будет равнодействующей
43
системы сил S. Таким образом, в этом случае |
система |
S |
||
приводится к одной силе – равнодействующей. |
|
|
||
5. R(S) ≠ 0, Mo(S) ≠ 0, R(S) не перпендикулярен Mo(S). Разложим |
|
|||
Mo(S) на две составляющие |
Mo/ и |
Mo// , причем |
Mo/ R(S) , |
а |
Mo// || R(S) (рис.42а). Эта |
процедура |
соответствует |
представлению |
|
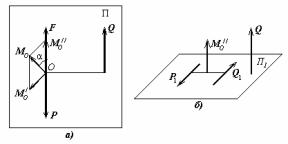
пары с моментом Mo(S) в виде двух пар: одну с моментом Mo/ , а вторую - с моментом Mo// . По тео-
реме о сложении пар эти пары эквивалентны исходной. Поскольку Mo/ (S) F (так как F = R(S)), то пара {P,Q}с таким
Рис.42 моментом может быть аналогично предыдущему случаю построена так, что F и Р окажутся
прямопротивоположными силами. После удаления их из трех сил F, Р и Q останется только сила Q. Однако есть еще пара сил {P1,Q1} с
моментом Mo// (рис.42б). Поскольку Mo// || Q (так как Q = F), то пара {P1,Q1} лежит в плоскости Π1, перпендикулярной Q. Система трех
сил {Q, P1, Q1}, две из которых P1, Q1 образуют пару, лежащую в плоскости, перпендикулярной третьему вектору Q, называется динамой. Таким образом, в этом случае система S приводится к
динаме.
§ 5. Простейшие системы сил
Поскольку частные случаи 1 – 5 теоремы Пуансо исчерпывают все логически возможные варианты значений R и Mo , можно сделать заключение о том, какие существуют типы простейших систем сил, к которым может быть приведена система сил S при помощи элементарных операций:
1.две прямопротивоположные силы (если R(S) = 0, Mo(S) = 0),
2.пара сил( если R(S) = 0, Mo(S) ≠ 0),
3.одна сила (равнодействующая) (если R(S) ≠ 0, Mo(S) = 0 либо
44
R(S) ≠ 0, Mo(S) ≠ 0, R(S) Mo(S)),
4.динама (если R(S) ≠ 0, Mo(S) ≠ 0, R(S) не перпендикулярен
Mo(S)).
Остается открытым вопрос: не может ли одна и та же система сил быть приведена к различным простейшим системам за счет выбора центра приведения? Для выяснения этого вопроса вводятся специальные величины, связанные с системами сил, именуемы инвариантами.
Инвариантами систем сил, называются величины (скалярные или векторные), которые не зависят от центра приведения этих систем к простейшему виду (т.е. являются характеристиками самих этих систем).
Таких инвариантов три:
1. первый инвариант I1 (S) = R (т.е. главный вектор системы
сил),
2.второй инвариант I2 (S) = (R, Mo) (т.е. скалярное произведение главного вектора на главный момент относительно центра приведения О),
3.третий инвариант I3 (S) = Mo, если R = 0 (т.е. главный момент системы сил, главный вектор которой равен нулю).
То, что I1 (S) действительно является инвариантом, очевидно. Убедимся, что I2 (S) является инвариантом. Для этого
воспользуемся формулой 13 параграфа 11 главы I:
|
|
|
|
|
|
|
Mo' |
= Mo +[O1O, R] . |
(32) |
||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
||
(R, Mo |
) = (R, Mo ) + (R,[O1O, R]) . |
(33) |
||||
1 |
|
|
|
|
|
|
Так как векторное произведение двух векторов представляет собой
вектор, |
перпендикулярный |
перемножаемым |
векторам, |
то |
||||
|
|
|
|
|
|
|
||
[O1O, R] R , а следовательно, |
(R,[O1O, R]) = |
0 как скалярное |
||||||
произведение двух взаимно перпендикулярных векторов. Из (33) получаем (R, Mo1 ) = (R, Mo ) для любых центров приведения О1 и О,
откуда и следует требуемое.
То, что I3 (S) является инвариантом, следует из формулы (32).
Теорема. Эквивалентные системы сил имеют равные инварианты.
Доказательство следует из того, что эквивалентные системы сил
45
имеют геометрически равные главные векторы и главные моменты относительно одного и того же полюса.
Следствие. Если система сил приводится при помощи элементарных операций к одной из простейших систем сил, то
она не может быть приведена к другой простейшей системе.
Доказательство. Найдем значения инвариантов простейших систем сил, используя частные случаи теоремы Пуансо и вышеприведенную теорему:
1.две прямопротивоположные силы:
I1 = R = 0, I2 = (R, Mo) = 0, I3 = Mo = 0;
2.пара сил:
I1 = R = 0, I2 = (R, Mo) = 0, I3 = Mo ≠ 0;
2.одна сила (равнодействующая):
I1 = R ≠ 0, I2 = (R, Mo) = 0 (так как либо Mo = 0, либо R Mo), I3 не существует, так как R ≠ 0,
3.динама:
I1 = R ≠ 0, I2 = (R, Mo) ≠ 0 (так как R ≠ 0, Mo ≠ 0 и R не перпендикулярен Mo), I3 не существует, так как R ≠ 0.
Просмотрев приведенные выше значения инвариантов простейших систем сил, можно отметить, что у любых двух из этих систем имеются несовпадающие значения по крайней мере одного инварианта. Отсюда следует, что одна и та же система сил не может быть приведена к двум различным простейшим системам , так как это значило бы, что они эквивалентны друг другу, что противоречит теореме.
Пользуясь приведенными выше значениями инвариантов простейших систем сил, легко сформулировать признаки приведения системы сил к равнодействующей и к динаме.
Признак приведения системы сил к равнодействующей. Для того чтобы система сил имела равнодействующую, необходимо и достаточно, чтобы R ≠ 0, (R, Mo) = 0, т.е. чтобы главный вектор
системы был отличен от нуля, а скалярное произведение главного вектора на главный момент равнялось нулю.
Признак приведения системы сил к динаме. Для того чтобы система сил приводилось к динаме, необходимо и достаточно, чтобы (R, Mo) ≠ 0, т.е. чтобы скалярное произведение главного
вектора на главный момент было отлично от нуля.
Здесь учтено, что из неравенства (R, Mo) ≠ 0 следует, что R ≠ 0.
46
Г Л А В А IV
ЦЕНТР ПАРАЛЛЕЛЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ
§ 1. Условие существования равнодействующей параллельных сил
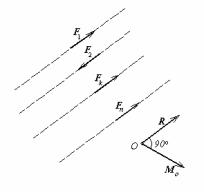
Рассмотрим систему |
параллельных сил S{F1,F2,…,Fn} (т.е. |
||||||
F1||F2||…||Fn) |
(рис.43). |
Главный |
вектор |
этой |
системы |
||
|
|
|
n |
|
|
|
|
|
|
R = ∑Fk |
параллелен |
линиям |
|||
|
|
k=1 |
|
|
|
|
|
|
|
действия сил, если он отличен от |
|||||
|
|
нуля. |
Момент |
каждой |
из сил |
||
|
|
mo(Fk) (k=1,2,…,n) перпендику- |
|||||
|
|
лярен линиям действия сил, так |
|||||
|
|
как он перпендикулярен плоскос- |
|||||
|
|
ти, |
проходящей |
через |
линии |
||
|
|
действия силы и полюс. Отсюда |
|||||
|
|
следует, |
что |
главный |
момент |
||
|
|
|
|
|
|
n |
|
|
|
системы сил Mo |
= ∑mo (Fk ) |
||||
|
|
|
|
|
|
k=1 |
|
|
Рис.43 |
перпендикулярен линиям дейст- |
|||||
|
|
вия сил. Таким образом, R Mo, |
|||||
а значит, (R , Mo) =0. Тогда признак существования равнодействующей (§5 предыдущей главы) для параллельных сил выглядит так:
Для того чтобы система параллельных сил имела равнодействующую, необходимо и достаточно, чтобы R ≠ 0, т.е.
чтобы ее главный вектор не равнялся нулю.
§ 2. Центр параллельных сил
Начнем с примера. Рассмотрим две параллельные силы F1 и F2, направленные в одну сторону (рис.44). Как показано в §17 главы I, положение точки приложения равнодействующей на отрезке АВ определяется равенством
AC |
= |
F2 |
. |
(34) |
|
|
|||
CB F1 |
|
|||
47

Повернем силы F1 и F2 вокруг их точек приложения А и В на один и тот же угол α с сохранением их величины и параллельности. Тогда равнодействующая также повернется на угол α , причем точка ее приложения на отрезке АВ останется неизменной, так как соотношение (34) остается справед-
Рис.44 ливым и для повернутых сил. Оказывается, подобная точка сущест-
вует и в более общем случае параллельных сил.
Центром параллельных сил называется точка приложения равнодействующей этих сил, вокруг которой равнодействующая поворачивается при повороте всех сил вокруг их точек приложения на один и тот же угол с сохранением параллельности.
Теорема. Если система параллельных сил имеет равнодействующую, то она имеет и центр параллельных сил, радиус-вектор которого определяется по формуле
|
|
n |
|
|
|
∑Fk rk |
|
r |
= |
k=1 |
(35) |
|
|||
c |
|
n |
|
|
|
∑Fk |
|
k=1
(здесь rk – радиус-вектор точки приложения силы Fk, а Fk = ±| Fk |, где знак выбирается в соответствии с правилом, приведенным в
доказательстве теоремы).
Доказательство.
|
|
Fk = Fk e (k = 1,2,…,n), (36) |
|
|
где |
Fk = ± | Fk |, где знак + выбирается |
|
|
в |
случае |
совпадения направлений |
|
векторов Fk |
и е, и знак – в противном |
|
|
случае. |
|
|
|
|
Пусть система S имеет равнодейст- |
|
|
вующую F. Тогда, используя представ- |
||
Рис.45 |
ление (36), можем записать |
||
48
n
где F = ∑Fk
k=1
F = F e, |
(37) |
, так как |
|
n |
n |
F = R = ∑Fk = |
∑Fk e . |
k=1 |
k=1 |
В соответствии с обобщенной теоремой Вариньона (§16 главы I) можно записать следующее равенство
n |
|
mo (F) = ∑mo (Fk ) |
(38) |
k=1 |
|
Используя представление момента силы относительно полюса в виде векторного произведения (§5 главы I), а также (36) и (37), можно представить (38) так:
n |
|
[rc , Fe] = ∑[rk , Fk e] |
(39) |
k=1 |
|
Перенося правую часть (39) налево и используя свойства |
|
векторного произведения, получаем |
|
n |
|
[Frc − ∑Fk rk , e] = 0 |
(40) |
k=1 |
|
Будем теперь поворачивать вектор е. Вследствие равенств (36) и |
|
(37) это приведет к повороту векторов |
Fk (k=1,2,…,n) и F с |
сохранением их параллельности. Будем |
полагать, что векторы Fk |
(k=1,2,…,n) поворачиваются вокруг их точек приложения, т.е. точки приложения этих сил, а значит, и радиус-векторы rk (k=1,2,…,n) останутся неизменными. Кроме того, так как мы разыскиваем центр параллельных сил, т.е. точку приложения равнодействующей, остающуюся неименной при поворотах сил, то и вектор rc тоже должен оставаться неизменным. Таким образом, левый множитель векторного произведения в (40) остается неизменным, в то время как правый множитель может поворачиваться произвольно. Отсюда следует, что сохранение равенства (40) при этом может соблюдаться только при
n |
|
Frc − ∑Fk rk = 0 |
(41) |
k=1 |
|
Из условия существования равнодействующей параллельных сил следует
49
n |
|
F = ∑Fk ≠ 0 |
(42) |
k=1
Сучетом этого неравенства из (41) получаем (35). Это равенство показывает, что центр параллельных сил существует, если выполнено неравенство (42), т.е. если существует равнодействующая.
Теорема доказана.
Спроектируем векторное равенство (35) на оси координат. Из соотношений
|
|
x = прx r, |
y = прy r, z = прz r |
|
||||||||
( r – радиус-вектор точки; x, y, z – ее координаты) получаем |
|
|||||||||||
|
|
n |
|
|
|
n |
|
|
|
n |
|
|
|
|
∑Fk xk |
|
|
|
∑Fk yk |
|
|
|
∑Fk zk |
|
|
xc |
= |
k=1 |
, |
yc |
= |
k=1 |
, |
zc |
= |
k=1 |
|
(43) |
n |
n |
n |
||||||||||
|
|
∑Fk |
|
|
|
∑Fk |
|
|
|
∑Fk |
|
|
|
|
k=1 |
|
|
|
k=1 |
|
|
|
k=1 |
|
|
Формулы (43) позволяют найти координаты центра параллельных сил.
§ 3. Центр тяжести
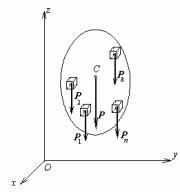
Центром тяжести тела называется центр параллельных сил тяжести элементарных масс, образующих тело, т.е. центр тяжести тела – это такая точка приложения равнодействующей сил тяжести элементарных масс, которая остается неизменной при любых поворотах тела. Под элементарными массами
понимаются массы |
малых частей (элементарных объемов),из |
||
|
которых состоит тело. |
|
|
|
На рис.46 изображено некоторое |
||
|
тело. Разобьем его на элементарные |
||
|
объемы (некоторые из них показаны |
||
|
на рисунке). Веса этих элементарных |
||
|
объемов |
(элементарных |
масс) |
|
образуют систему параллельных сил. |
||
|
Очевидно, они имеют равнодейству- |
||
|
ющую, так как они направлены в |
||
|
одну сторону, и их сумма не может |
||
|
равняться нулю. Следовательно, су- |
||
|
ществует |
центр этих параллельных |
|
|
сил, т.е. центр тяжести тела. Его ко- |
||
Рис.46 |
ординаты могут быть найдены из |
||
50
