
Курс теоретической механики 2007 (Рус)
.pdfвыполнялись уравнения равновесия:
n |
n |
n |
|
|
1) ∑прx Fk = 0, 2) |
∑прy Fk |
= 0, 3), ∑прz Fk = 0, |
|
|
k=1 |
k=1 |
k=1 |
(17) |
|
n |
n |
n |
||
|
||||
4) ∑mx Fk = 0, 5) |
∑my Fk = 0, 6) ∑mz Fk = 0. |
|
||
k=1 |
k=1 |
k=1 |
|
|
Доказательство.
Найдем проекции главного вектора и главного момента на оси координат
n |
n |
|
Rx = прx R = прx ∑Fk = ∑прx Fk , |
|
|
k=1 |
k=1 |
|
n |
|
|
Ry = ∑прy Fk , |
|
|
k=1 |
|
|
n |
|
|
Rz = ∑прz Fk , |
|
|
k=1 |
|
(18) |
|
|
|
n |
n |
n |
M ox = прx Mo = прx ∑mo (Fk ) = ∑прx mo (Fk ) = ∑mx (Fk ), |
||
k=1 |
k=1 |
k=1 |
n
M oy = ∑my (Fk ), k=1
n
M oz = ∑mz (Fk ). k=1
При выводе последних трех равенств мы воспользовались теоремой о проекции суммы векторов на ось (см. Добавление 1), а также зависимостью между моментами силы относительно полюса и оси.
Равенство нулю главного вектора и главного момента эквивалентно равенству нулю их проекций на все оси координат. Тогда из основной теоремы статики вытекает, что для того чтобы тело находилось в равновесии, необходимо и достаточно, чтобы выполнялись следующие равенства:
Rx = 0, Ry = 0, Rz = 0, Mox = 0, Moy = 0, Moz = 0. |
(19) |
31
Подставив сюда выражения для проекций главного вектора и главного момента из (18), получаем требуемое. Теорема доказана.
§ 4. Аналитические условия равновесия для частных случаев системы сил
1. Сходящиеся силы. Силы называются сходящимися, если
линии действия сил пересекаются в одной точке, называемой точкой схода (рис. 32).
Выберем начало координат О в точке схода. Тогда моменты всех сил относительно полюса О будут равны нулю (см. §4 главы I), а следовательно, будет равен нулю главный момент системы сил относительно этого полюса. Отсюда вытекает, что три последних уравнения (17) удовлетворяются тождественно, и
уравнениями равновесия для сходящихся сил являются следующие уравнения:
n |
|
1) ∑прx Fk |
= 0, |
k=1 |
|
n |
|
2) ∑прy Fk |
= 0, (20) |
k=1 |
|
n |
|
3) ∑прz Fk |
= 0. |
k=1
Равенства (20) выражают равенство нулю проекций главного вектора R на оси
Рис.32 координат, а значит и равенство нулю самого
главного вектора. Таким образом, для того чтобы тело под
действием сходящихся сил находилось в равновесии, необходимо и достаточно, чтобы главный вектор этих сил равнялся нулю.
2.Параллельные силы.
Рассмотрим систему параллельных сил (рис.33). Выберем систему координат следующим образом:
ось z направим параллельно линиям действия сил, тогда оси x и y окажутся им перпендикулярными. Тогда проекции всех сил на оси x и y будут равны нулю, т.е. первых два уравнения (17) удовлетворяются тождественно. Кроме того, моменты всех сил относительно оси z
32
также равны нулю, так как их линии действия параллельны этой оси. Поэтому и шестое уравнение (17) удовлетворяется тождественно.
Таким образом,
уравнениями равновесия параллельных сил являются следующие уравнения:
n |
|
1) ∑прz Fk |
= 0, |
k=1 |
|
n |
|
2) ∑mx Fk |
= 0, (21) |
k=1 |
|
n |
|
3) ∑my Fk |
= 0. |
k=1
Рис.33
3.Плоская система сил.
Пусть система сил расположена в плоскости Π. Проведем оси x и y в этой плоскости, а ось z – перпендикулярно ей. Очевидно, линии действия всех сил перпендикулярны оси z, поэтому проекции всех сил на ось z равны нулю, т.е. третье уравнение (17) удовлетворяется тождественно. Кроме того, моменты всех сил относительно осей x и y
Рис.34 равны нулю, так как эти оси лежат в одной плоскости с силами, а следовательно, линии действия сил либо параллельны этим
осям, либо их пересекают. Таким образом, четвертое и пятое уравнения (17) также удовлетворяются тождественно, и уравнениями
равновесия плоской системы сил являются следующие уравнения:
33
n |
n |
n |
|
1) ∑прx Fk |
= 0, 2) ∑прy Fk |
= 0, 3) ∑mz Fk = 0, |
(22) |
k=1 |
k=1 |
k=1 |
|
Пример 1. Определение опорных реакций балки, находящейся
|
под |
действием |
|
плоской системы |
|
|
сил. |
|
|
На рис.35 изоб- |
|
|
ражена |
изогнутая |
|
балка, |
находяща- |
|
яся под действием |
|
|
сил Р1 и Р2 , а |
|
|
также пары сил с |
|
|
моментом М. Все |
|
Рис.35 |
эти силы лежат в |
|
|
одной |
плоскости, |
совпадающей с плоскостью чертежа. Заданы следующие величины: Р1 =10 кН, Р2 =4 кН, М = 5 кНм, α = 30о. Необходимо найти реакции неподвижного шарнира А и стержня В (ось шарнира перпендикулярна
плоскости, в которой лежат силы).
Решение. В параграфе 20 главы I было показано, что реакция неподвижного шарнира RA раскладывается на две составляющие RAx и RAy в плоскости, перпендикулярной оси шарнира, т.е. в плоскости чертежа. Реакция стержня RВ направлена вдоль оси стержня, т.е. в данном случае вертикально. В результате добавления этих сил к заданным, получаем систему сил, показанную на рис. 34. Балка находится в равновесии под действием этой системы сил. Поэтому выполняются уравнения равновесия для плоской системы сил. Для того, чтобы упростить их составление, разложим силу Р2 на две
составляющие: |
P/ |
= Р2 sin α и P// = Р2 cos α. Составим уравнения: |
|
2 |
2 |
n |
|
|
∑прx Fk |
=RAx + P2 sin α = 0 |
|
k=1 |
|
|
n |
|
|
∑прy Fk |
= RAy − P1 + RB − P2 cos α = 0 |
|
k=1 n
∑mz (Fk ) = M − 4P1 + 5RB −8P2 cos α − 2P2 sin α = 0
k=1
34
При составлении последнего уравнения было учтено, что ось z перпендикулярна плоскости чертежа, т.е. все силы лежат в плоскости, перпендикулярной этой оси, и при вычислении моментов относительно этой оси можно использовать упрощенное правило (см. свойство 3 из §3 главы I).
Из последнего уравнения находим
RB = |
−M + 4P1 + 8P2 |
cos α + 2P2 |
sin α |
= 13,34 кН. |
|
5 |
|
||
|
|
|
|
Из первого уравнения получаем
RAx = - P2 sin α =- 2 кН,.
А из второго
RAy = P1 – RB + P2 cos α = 0,12 кН.
Так как RA = RAx +RAy , то RA = 
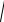 RAx2 + RAy2 = 2,004 кН.
RAx2 + RAy2 = 2,004 кН.
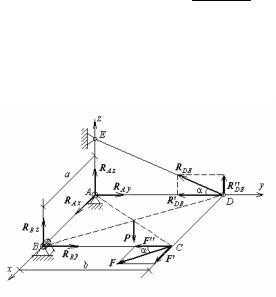
Пример 2. Определение опорных реакций плиты, находящейся под действием пространственной системы сил.
Однородная прямоугольная плита ABCD весом Р = 10 кН опирается на неподвижный сферический шарнир в точке А (рис.36). В точке В ее поддерживает неподвижный цилиндрический шарнир, ось которого совпадает с осью х, а в точке D – стержень DE. В точке С на нее действует сила F = 20 кН в плоскости плиты под углом α к
Рис.36 ребру ВС. Необходимо найти реакции
опор плиты, если α = 30о и b/a = 2.
35
Решение. В §20 главы I было показано, что реакция сферического шарнира RA имеет три составляющие RAx , RAу , RAz вдоль трех осей координат х,у и z, а реакция RВ – две составляющие RВу и RВz в плоскости, перпендикулярной оси шарнира, т.е. оси х. Реакция RDE стержня DE должна быть направлена вдоль оси стержня. Разложим
реакцию стержня RDE на две составляющие RDE/ = RDE cosα и RDE// =
=RDE sinα, параллельные осям y и z. Аналогично раскладывается сила F: на силу F/ = F sinα, параллельную оси х, и силу F// = F cosα, параллельную оси у. Таким образом, плита находится в равновесии под действием пространственной системы сил, показанной на рис 36. Составляем уравнения равновесия:
n |
|
|
|
|
|
∑прx Fk |
=RAx + F sin α = 0, |
||||
k=1 |
|
|
|
|
|
n |
|
|
|
|
|
∑прy Fk = RAy + RBy − RDE cos α − F cos α = 0, |
|||||
k=1 |
|
|
|
|
|
n |
|
|
|
|
|
∑прz Fk |
=RAz + RBz + RDE sin α − P = 0, |
||||
k=1 |
|
|
|
|
|
n |
|
|
|
|
|
∑mx |
(Fk ) = bRDE sin α − |
b |
P = 0, |
||
|
|||||
k=1 |
2 |
|
|||
|
|
|
|
|
|
n |
|
|
|
|
|
∑my |
(Fk ) = − aRBz + |
a |
P = 0, |
||
|
|||||
k=1 |
2 |
|
|
|
|
|
|
|
|
|
|
n
∑mz (Fk ) = aRBy − aF cos α − bF sin α = 0.
k=1
Из первого уравнения находим
RAx = - F sinα = -10 кН.
Из четвертого уравнения:
RDE = Р = 10 кН.
Из пятого уравнения:
36

RBz = Р/ 2 = 5 кН.
Из шестого уравнения:
RВу = F cosα + b F sin α = 37,3 кН. a
Подставив найденные значения реакций во второе и третье уравнения, находим
RAy = - RBy +RDE cosα +F cosα = 8,67 кН, RAz = - RBz - RDE sinα +P = 0.
Так как RA = RAx + RAy + RAz , то
RA = 
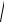 RAx2 + RAy2 + RAz2 = 13,23 кН.
RAx2 + RAy2 + RAz2 = 13,23 кН.
Так как RВ = RВy + RВz , то
RB = 
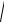 RBy2 + RBz2 = 37,63 кН.
RBy2 + RBz2 = 37,63 кН.
37
Г Л А В А III
ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
§ 1. Общий признак эквивалентности систем сил
Теорема. Для того чтобы две системы сил S1{F1,F2,…,Fn} и S2{Р1,Р2,…,Рm} были эквивалентными, необходимо и достаточно,
чтобы их главные векторы и главные моменты относительно одного и того же полюса были геометрически равны.
Необходимость условий эквивалентности (т.е. то, что из эквивалентности двух систем сил следует равенство их главных векторов и главных моментов относительно одного и того же полюса ) следует непосредственно из свойства 3 эквивалентных систем сил (§15 главы I).
Докажем достаточность условий эквивалентности (т.е. что из равенств
R(S1) = R(S2), Mo(S1) = Mo(S2) |
(23) |
следует S1 ~ S2 ).
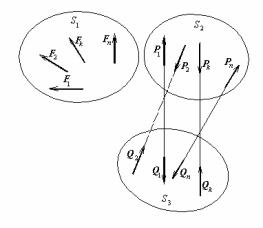
|
Введем дополни- |
||
|
тельную |
систему |
|
|
сил S3{Q1,Q2,…,Qm}, |
||
|
силы которой |
прямо- |
|
|
противоположны |
си- |
|
|
лам |
системы |
|
|
S2{Р1,Р2,…,Рm} и рас- |
||
|
смотрим систему S, со- |
||
|
стоящую из сил, вхо- |
||
|
дящих во все три сис- |
||
|
темы S1 , S2 и S3, т.е. |
||
|
S = S1 U S2 U S3 . (24) |
||
|
Поскольку системы |
||
|
S2 и S3 с остоят |
из |
вза- |
Рис.37 |
имно прямопротиво- |
||
|
положных сил, то |
ис- |
|
пользуя m раз вторую элементарную операцию, их можно удалить. В результате от системы S останется только система сил S1, т.е. эта сис-
38
тема была получена из системы S при помощи элементарных операций. Это значит, что
S1 ~ S. |
(25) |
Рассмотрим теперь систему S4, состоящую из сил, входящих в |
|
системы S1 и S3, т.е. |
|
S4 = S1 U S3 . |
(26) |
Заметим, что при этом из (24) следует, что |
|
S = S2 U S4 . |
(27) |
Найдем главный вектор системы S4: |
|
R(S4) = R(S1) + R(S3), |
(28) |
Так как {Pk,Qk} – п.п.с., т.е. Pk = − Qk (k = 1,2,…,n) , то |
R(S3) = |
=−R(S2). Но по условию R(S2) = R(S1) . Таким образом, R(S3) = − R(S1), и из (28) получаем
R(S4) = 0.
Совершенно аналогично доказывается, что
Mo(S4) = 0.
Используем теперь основную лемму статики и при помощи элементарных операций приведем систему S4 к двум силам P и Q. Из свойства 3 эквивалентных систем сил (§15 главы I) следует, что
P + Q = R(S4) = 0,
mo(P) +mo(Q) = Mo(S4) = 0.
Такими свойствами обладают только две прямопротивоположные силы, т.е. {P,Q} – п.п.с. Используем теперь вторую элементарную операцию и удалим эти силы. Напомним, они были получены из S4 при помощи элементарных операций. Таким образом, система S4 исчезает и от системы S (см.(26)) остается только система S2. Это значит, что
S ~ S2 .
39
Сопоставляя это соотношение с (25) и используя свойство 2 эквивалентных систем сил (§15 главы I), получаем
S1 ~ S2
(что и требовалось доказать).
Следствие 1 (признак эквивалентности пар). Для того чтобы две пары сил были эквивалентными, необходимо и достаточно,
чтобы их моменты были геометрически равны.
Доказательство. Главный вектор пары сил равен нулю, таким образом условие геометрического равенства главных векторов любых пар сил выполнено. Отсюда вытекает, что необходимым и достаточным условием эквивалентности пар сил является геометрическое равенство их моментов.
Следствие 2 (теорема о сложении пар). Система пар сил эквивалентна а) паре сил, момент которой равен геометрической сумме
моментов пар, входящих в систему, в том случае, когда эта геометрическая сумма отлична от нуля; б) двум прямопротивоположным силам, если геометрическая
сумма моментов пар равна нулю.
Доказательство.
Случай а). Главный вектор системы пар сил S{P1,Q1,P2,Q2,…,Pm,Qm} равен нулю, так как главный вектор каждой из них равен нулю, т.е. Pi+Qi = 0 (i=1,2,…,m). Таким образом главные векторы системы пар и одной пары сил геометрически равны всегда. Поэтому для эквивалентности системы пар сил S{P1,Q1,P2,Q2,…,Pm,Qm}одной паре S1{P,Q}достаточно выполнение условия геометрического равенства их главных моментов, т.е. равенства геометрической суммы моментов пар, входящих в систему S{P1,Q1,P2,Q2,…,Pm,Qm}, моменту пары S1{P,Q}, который отличен от нуля (см. §12 главы I).
Случай б). Если геометрическая сумма моментов пар, образующих систему S{P1,Q1,P2,Q2,…,Pm,Qm}, равна нулю, то тем самым выполняются два условия
R(S)=0, M(S)=0.
Но таким же условиям удовлетворяют и две прямопротивополож-
40
