Курс теоретической механики 2007 (Рус)

движение ее относительно подвижной системы координат хАу – относительным, а движение подвижной системы координат хАу

как и ось, проходящая через эту точку и перпендикулярная плоскости По. Таким образом, плоскопараллельное движение тела

представлено в виде суперпозиции (наложения) двух движений : переносного - поступательного и относительного – вращения вокруг неподвижной оси. Точка А плоской фигуры, являющаяся началом подвижной системы координат, называется полюсом разложения плоскопараллельного движения тела на поступательное и вращательное.

Для записи уравнений плоскопараллельного движения тела необходимо, очевидно, составить уравнения переносного и относительного движений. Поступательное движение определяется движением одной точки тела (например, точки А), а вращение – угловой координатой, которую можно задать как угол между осью х и каким либо отрезком АВ плоской фигуры (рис.30). Таким образом,

§ 2. Независимость угловой скорости относительного вращения от выбора полюса разложения

Теорема. Угловая скорость относительного вращения не

зависит от выбора полюса разложения.

Доказательство. Возьмем два различных полюса разложения А1 и А2 , затем – некоторую точку плоской фигуры В (рис.31). При выборе

92

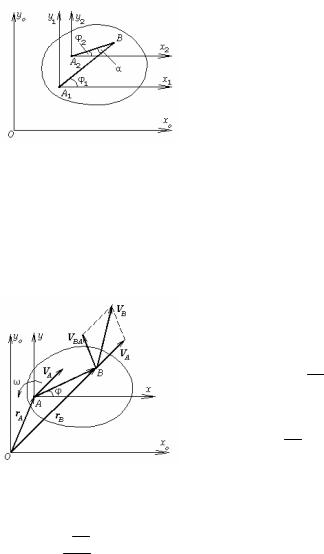
полюса А1 относительное вращение определяется углом φ1 между осью х1 и отрезком А1В, а при выборе полюса А2 – углом φ2 между осью х2 и отрезком А2В. Из чертежа следует,

что

где α – угол между отрезками А1В и А2В. Заметим, что α = const, так как точки А1 , А2 и В являются точками плоской фигуры, полученной пересечением абсолютно твердого тела плоскостью По. Дифференцируя (82) по времени, получим

Рис.31

ω1 = ω2,

что и требовалось.

§ 3. Вторая формула Эйлера

Пусть А – полюс разложения плоскопараллельного движения на поступательное и вращательное, а В – точка плоской фигуры (рис.32). Из рисунка следует, что

Здесь rA и rB – радиус-векторы точек А и В в неподвижной системе

координат, а AB – радиус-вектор точки В в подвижной системе коор -

Рис.32 динат. Продифференцировав (83) по времени получим

где VBA = d AB , что представляет собой скорость точки В в относи- dt

93

тельном вращении плоской фигуры вокруг оси Аz, перпендикулярной плоскости чертежа и проходящей через точку А.

Таким образом, скорость любой точки плоской фигуры равна

скорости произвольно выбранного полюса, геометрически сложенной со скоростью этой точки в относительном вращении плоской фигуры вокруг оси, перпендикулярной фигуре и проходящей через полюс.

Используя первую формулу Эйлера (§5 главы II), можем записать

так как ω AB .

Замечание. Скорость VBA = [ω, AB ] перпендикулярна AB , так

как векторное произведение перпендикулярно каждому из перемножаемых векторов.

Тогда (84) можно записать так:

Формула (87) (или же две формулы (84) и (85)) и представляет собой вторую формулу Эйлера.

Следствия.

Если скорости двух точек плоской фигуры геометрически равны в какой-то момент времени, то скорости всех точек плоской

фигуры геометрически равны в этот момент времени.

Доказательство. Пусть VB = VA . Из (84) и (86) имеем ω = 0. Возьмем теперь произвольную точку С плоской фигуры и запишем для нее вторую формулу Эйлера (87):

VС = VA + [ω, AC ] = VA ,

откуда и следует справедливость следствия.

Если скорости всех точек плоской фигуры становятся геометрически равными в какой-то момент времени, то говорят, что фигура совершает мгновенно поступательное движение в этот

94

момент.

1)Проекции скоростей двух точек плоской фигуры на ось,

проходящую через эти точки, равны.

Доказательство. Спроектируем равенство (84) на направление вектора AB . Учитывая, что VBA AB , получаем

npAB VA = npAB VB ,

что и требовалось.

§ 4. Мгновенный центр скоростей (мгновенный центр вращения)

Теорема. Если угловая скорость относительного вращения отлична от нуля в какой-то момент времени, то существует точка, причем единственная, скорость которой равна нулю в этот

момент времени.

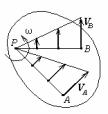
Доказательство. Пусть скорость некоторой точки А плоской фигуры равна VA (рис.33). Проведем перпендикуляр к VA через точку

Вектор VPA перпендикулярен отрезку АВ, а значит, параллелен вектору VA . Учитывая направление относительного вращения (см.

Эйлера для нахождения скорости точки Р:

Рис.33

VP = VA + VPA = 0

Докажем, что точка плоской фигуры, скорость которой равна нулю в данный момент времени единственна. Допустим противное, т.е. что существует еще одна точка Р/ плоской фигуры, скорость которой также равна нулю в этот момент времени, т.е. VP’ = 0. Тогда

95

оказывается, что VP’ = VP = 0 , и по первому следствию из второй формулы Эйлера получаем, что скорости всех точек плоской фигуры обратились в нуль, т.е. фигура остановилась и угловая скорость ω в этот момент времени также оказалась равной нулю, что противоречит условию теоремы. Это значит, что наше допущение о неединственности точки с нулевой скоростью неверно.

Теорема доказана. Введем определение:

Точка плоской фигуры , скорость которой равна нулю в данный момент времени называется ее мгновенным центром скоростей (при условии, что эта точка единственна).

§ 5. Картина распределения скоростей точек плоской фигуры

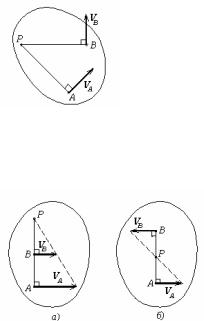
Возьмем в качестве полюса разложения мгновенный центр скоростей Р. Тогда вторая формула Эйлера для произвольной точки А плоской фигуры запишется так:

VА = VР + VAР = VAР ,

так как VР = 0. Таким образом, скорость точки Рис.34 плоской фигуры совпадает со скоростью относи-

тельного вращения фигуры вокруг мгновенного центра скоростей. Учитывая замечание в §3 и формулу (86), приходим к заключению, что имеют место два утверждения:

1)скорости точек плоской фигуры перпендикулярны отрезкам, соединяющих их с мгновенным центром скоростей;

2)величины скоростей точек плоской фигуры пропорциональны длинам отрезков, соединяющих их с мгновенным центром скоростей.

Всоответствии с этими правилами построена картина

распределения скоростей точек плоской фигуры (рис.34). Она совпадает с картиной распределения скоростей точек фигуры, вращающейся вокруг оси, перпендикулярной плоскости фигуры и проходящей через мгновенный центр скоростей. Поэтому мгновенный центр скоростей носит еще название мгновенного центра вращения.

96

§ 6. Построение мгновенного центра скоростей

Рассмотрим построение мгновенного центра скоростей в различных частных случаях.

1. Скорости двух точек плоской фигуры не параллельны. Используя утверждение 1 предыдущего параграфа, приходим к

выводу, что мгновенный центр скоростей находится в точке пересечения перпендикуляров к скоростям. Таким образом,

если скорости двух точек плоской фигуры не паралллельны, то для нахождения мгновенного центра скоростей необходимо провести перпендикуляры к ско-

2.Скорости двух точек плоской фигуры перпендикулярны отрез

ных в некотором масштабе.

3. Скорости двух точек плоской фигуры геометрически равны (т.е. VA = VB). Как вытекает из первого следствия из второй формулы Эйлера, в этом случае фигура совершает мгновенно поступательное движение и мгновенный центр скоростей не существует (рис.37).

97

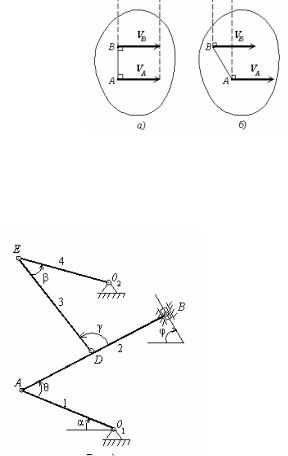
Рис.37

§7. Определение скоростей точек плоского механизма

Задача. Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и опорами О1 и О2 шарнирами (рис. 38).

Дано α=60ο, β=150ο, γ=90ο, φ=60ο,

θ=30ο, l1=0,4м, l2=1,2м, l2=1,4м, l3=1,4м, l4=0,6м, ω1=2с-1.

Необходимо найти ωАВ, VВ, VE.

Решение.

Решение начинаем с построения положения механизма в соответствии с заданными углами. Построение начинаем с угла α – откладываем его от горизонтали против часовой стрелки. Вдоль полученного направления откладываем в масштабе l1. В результате получаем положение точки А. От полученного направления стерж-

Рис.38 ня 1 откладываем против часовой стрелки (как указано на чертеже) угол β и получаем направление стержня 2. Отложив в этом

направлении длину l2, находим положение точки В и так далее (заметим только, что точка D – середина стержня 2). Результат этого построения приведен на рис. 39).

Стержень О1А вращается вокруг неподвижной оси, перпендикулярной плоскости чертежа и проходящей через точку О1. Скорость точки А направлена перпендикулярно стержню О1А, так как она движется по окружности, центр которой находится в точке О1.

98

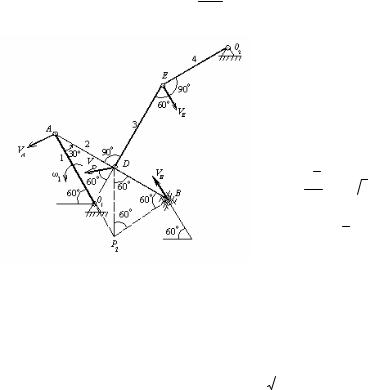
Величина определяется по формуле для скорости точки вращающегося тела

VA = ω1l1 = 0,8 м/с2.

Скорость точки В направлена вдоль оси ползуна, т.е. под углом 30о к горизонтали. Таким образом, известны направления скоростей двух точек стержня АВ. Они не параллельны друг другу. Поэтому мгновенный центр скоростей этого стержня Р2 находится на пересечении перпендикуляров к скоростям точек А и В. Угловая скорость стержня АВ определяется по формуле

ωAB = VA

AP2

Длина отрезка АР2 может быть найдена из треугольника АВР2. Он прямоугольный, так как отрезок ВР2 проведен перпендикулярно VB, а она параллельна АР2.

Тогда

AP2 = AB cos300 =

3

= l2 2 = 0,6 3м

Следовательно, ωAB = 4 / 33 с-1.

Заметим, что треугольник DBP2 равносторон-

Рис.39 ний, так как DB=l2 / 2, поскольку точка D –

середина отрезка АВ, и ВР2=l2 / 2 как катет, противолежащий углу 30о. Кроме того, угол между этими отрезками равен 60о. Отсюда следу-

ет, что

Нетрудно выяснить, что вектор VD образует угол 60о с направлением отрезка ЕD. Кроме того, вектор VE также образует угол 60о с отрезком ED, так как VE O2 E , а угол O2ED равен 150о. Тогда

99

из следствия из второй формулы Эйлера, которое заключается в том, что проекции скоростей двух точек плоской фигуры на прямую, проходящую через эти точки, равны, следует

VD cos600 = VE cos600 , т.е. VE = VD = 0,462 м/с2

100