
Курс теоретической механики 2007 (Рус)
.pdf
кинетическая энергия произвольно движущегося твердого тела равна кинетической энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг оси мгновенного вращения, проходящей через центр масс.
§17. Пример решения задачи с использованием теоремы об изменении кинетической энергии
Задача. Эпициклический механизм |
состоит из трех зубчатых |
|||||
|
колес одинакового радиуса R = 1 м |
|||||
|
(рис.43), |
одно |
из |
|
которых |
|
|
неподвижно, |
и |
кривошипа, |
|||
|
вращающегося |
|
вокруг |
оси, |
||
|
проходящей |
|
через |
|
центр |
|
|
неподвижного |
колеса. |
Движущиеся |
|||
|
колеса прикреплены к |
кривошипу |
||||
|
при помощи осей, проходящих через |
|||||
|
центры колес. В процессе движения |
|||||
|
механизма |
под |
действием сил |
|||
|
тяжести из начального вертикального |
|||||
|
положения |
покоя |
кривошип |
|||
|
приобретает |
угловую |
|
скорость, |
||
|
зависящую от угла φ между верти- |
|||||
Рис.43 |
калью и осью кривошипа. |
Опреде- |
||||
|
лить угловую скорость, которую |
|||||
приобретет кривошип в тот момент, когда угол φ станет равным 90о. Масса кривошипа m1 = 5 кг, а масса колес m2 = 2 кг. Колеса считать однородными дисками.
Решение. Для решения задачи используем теорему об |
измене- |
нии кинетической энергии механической системы: |
|
T1 − T0 = Ae + Ai. |
(147) |
Будем полагать, что связи, образующие систему из отдельных тел, а также образующие тела из отдельных частиц, идеальны (более подробно об идеальных связях см. следующую главу). Они характерны тем, что работа их реакций равна нулю. В нашем случае это означает, что работа внутренних сил равна нулю:
161
Аi = 0. |
(148) |
Кроме того, из условия следует, что
Т0 = 0. |
(149) |
Для нахождения кинетической энергии системы в конечном положении необходимо выяснить, какое движение совершает каждое из тел.
Кривошип вращается вокруг неподвижной оси, проходящей через точку О. Поэтому его кинетическая энергия определяется по формуле
T (1) = |
J (1) |
ω2 |
||
z |
1 |
. |
||
2 |
||||
|
|
|||
Так как кривошип представляет собой стержень, то его момент инерции равен
J z(1) = |
m l 2 |
|
m |
(4R)2 |
|
|
16m R2 |
|
|||||
1 |
|
= |
|
|
1 |
|
|
= |
1 |
. |
|
||
3 |
|
|
|
|
3 |
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T (1) |
= |
8m R2 |
ω2 |
|
|
|
|
||||
|
|
|
1 |
1 |
|
. |
|
(150) |
|||||
|
|
|
3 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скорость центра колеса II можно выразить через угловую скорость кривошипа, так как точка С2 является одновременно точкой кривошипа
VC |
= ω1 2R . |
(151) |
|
2 |
|
Колесо II катится по неподвижному колесу I. Так как проскальзывание при этом отсутствует, то скорость точки D колеса II, находящаяся в соприкосновении с колесом I, равна нулю: VD = 0. Это значит, что точка D является мгновенным центром скоростей колеса II. Угловая скорость колеса равна:
ω2 = |
VC |
2 |
= 2ω1 . |
(152) |
|
R |
|||||
|
|
|
|||
Так как колесо совершает плоское движение, то его кинетическая энергия определяется по формуле
162
T (2) = |
m2VC2 |
JC(2)ω |
22 |
|
|
|
2 |
+ |
2 |
|
. |
(153) |
|
2 |
2 |
|
||||
|
|
|
|
|
||
Колесо является однородным сплошным диском, поэтому
J (2) = |
m2 R2 |
. |
(154) |
C |
2 |
2 |
|
|
Подставляя (151), (152) и (154) в (153), будем иметь
T (2) = 2m2ω12 R2 + m2ω12 R2 = 3m2ω12 R2 . |
(155) |
Найдем скорость точки Е колеса II. Так как мгновенный центр скоростей находится в точке D, то
VE = ω2 2R = 4ω1R . |
(156) |
Рассмотрим теперь движение колеса III. Скорость центра колеса равна:
VC |
= ω1 4R . |
(157) |
|
3 |
|
Так как проскальзывание между колесами II и III отсутствует, то скорость точки Е колеса III также определяется из (156). Сопоставляя формулы (156) и (157), а также используя следствие из второй формулы Эйлера для плоскопараллельного движения, приходим к выводу, что колесо III совершает поступательное движение. Поэтому его кинетическая энергия определяется по формуле
2 |
|
|
|
T (3) = |
m2VC3 |
= 8ω12 R2 . |
(158) |
|
|||
2 |
|
|
|
Складывая Т(1), Т(2) и Т(3), получаем кинетическую энергию системы в конечном положении
Т1 |
= ( |
8m1 |
+11m2 ) ω12 R2 . |
(159) |
|
||||
|
3 |
|
|
|
Перейдем к определению работы внешних сил. Поскольку это силы тяжести, то для вычисления работы используем формулу (126). Вес кривошипа и вес колеса II приложены в точке С2 . Легко выяснить, что перемещение этой точки по вертикали (см. рис.43) равно
h2 = 2R .
Вес колеса III приложен в точке С3 , перемещение которой по вертикали равно
163

h3 = 4R .
Отсюда следует, что работа внешних сил равна:
Ae = (P1 + P2 ) 2R + P3 4R = (2m1 +6m2 ) gR. |
(160) |
Подставляя (148), (149), (159) и (160) в (147), получаем
(8m1 +11m2 )ω12 R2 = 2(m1 + 3m2 )gR , 3
откуда находим
ω1 = 2(m1 + 3m2 )g = 2,47 с−1. (8m1 +11m2 )R
3
164

Г Л А В А III
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
§1. Связи
Механическая система называется свободной, если на перемещения ее точек и их скорости не наложены никакие ограничения. В противном случае система называется несвободной.
Ограничения, накладываемые на перемещения и скорости точек несвободной механической системы, называются связями.
Математически связи могут быть выражены при помощи равенств или неравенств (что будет видно из примеров, приведенных ниже).
Приведем классификацию связей.
а) Связи делятся на удерживающие и неудерживающие. Удерживающими называются связи, математическое
выражение которых представляет собой равенство. В противном случае связи называются неудерживающими.
Пример 1. Приведем пример удерживающей связи. Пусть две материальные точки соединены друг с другом при помощи абсолютно твердого стержня длиной l (рис.44).
Как известно из курса аналитической геометрии, расстояние между двумя точками определяется по формуле
|
| M1M2 | = |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.44 |
= (x |
2 |
− x )2 |
+ (y |
2 |
− y )2 |
+ (z |
2 |
− z |
1 |
)2 |
, |
|
|
|
|
1 |
|
1 |
|
|
|
|
||||
где xj , yj , zj − координаты точки Mj (j = 1,2).
Тогда математическое выражение стержня будет выглядеть так
| M1M2 | = l ,
т.е.
(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2 = l2 . |
(161) |
165
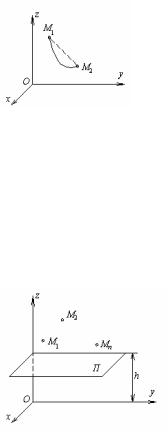
Таким образом, стержень являет собой пример удерживающей связи.
Пример 2. Приведем пример неудерживающей связи. Пусть теперь две материальные точки соединены при помощи нерастяжимой нити, длина которой равна l (рис.45).
Очевидно, математическое выражение связи в этом случае выглядит так
| M1M2 | ≤ l ,
или
(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2 ≤ l2 . (162)
Таким образом, нить является неудерживающей связью.
Рис.45
б) Связи делятся на стационарные и нестационарные. Стационарными называются связи, математическое
выражение которых не содержит времени t явно. В противном
случае связи называются нестационарными.
Очевидно, вышеприведенные примеры связей представляют собой
стационарные связи.
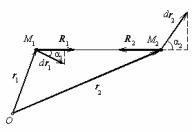
Пример 3. Приведем пример нестационарной связи. Пусть перемещения точек M1,M2,…,Mп механической системы ограничены снизу плоскостью П, высота которой h над координатной плоскостью хОу
меняется с течением времени
|
h = 2 t2 . |
|
|
Очевидно, математическое |
выражение |
|
связи выглядит так |
|
|
zi ≥ 2 t2 (I = 1,2,…,n) |
(163) |
Рис.46 |
( zi – аппликаты точек механичес |
|
|
кой системы). Неравенства (163) |
|
показывают, что плоскость П является нестационарной связью.
в) Связи делятся на геометрические и кинематические. Геометрическими называются связи, ограничивающие только
перемещения точек. В противном случае (т.е. когда связи
166
ограничивают еще и скорости точек) связи называются кинематическими.
Признаком геометрической связи является отсутствие производных координат точек механической системы по времени. Таким образом, все вышеприведенные примеры связей являются геометрическими. Приведем пример кинематической связи.
Пример 4. В автомобиле начинающего водителя установлено устройство, отключающее двигатель всякий раз, когда скорость автомобиля достигает некоторой заданной величины Vд. Таким образом, для скорости автомобиля выполняется неравенство
V ≤ Vд. |
(164) |
Полагая, что автомобиль является материальной точкой, перемещающейся в плоскости хОу, неравенство (164) можно записать так
& 2 |
& 2 |
2 |
, |
(165) |
x |
+ y |
≤ Vд |
т.е. в этом случае математическое выражение связи содержит производные координат точки по времени.
§2. Идеальные связи
Связи называются идеальными, если элементарная работа реакций связей на любом бесконечно малом перемещении механической системы, допускаемом этими связями, равна нулю.
Примеры идеальных связей.
1.Стержень. Покажем, что абсолютно твердый невесомый
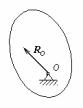
стержень является идеальной связью. Пусть две материальные точки М1 и М2 соединены при помощи стержня. Реакции стержня R1 и R2 являются прямопротивопо-
ложными силами: R2 = − R1. Очевидно,
|
|
|
|
|
|
M1M2 = r2 − r1 (166) |
|
|
( rj − радиус-вектор точки Мj , |
||
Рис.47 |
j =1,2). Умножим равенство (166) |
||
|
скалярно само на себя |
||
167
|
|
2 |
|
|
|
||
(r2 − r1, r2 − r1 ) =| M1M 2 | . |
(167) |
||
Так как стержень М1М2 абсолютно твердый, то правая часть равенства (167) является постоянной величиной. Возьмем дифференциал от левой и правой частей этого равенства:
|
|
|
|
|
|
(r2 − r1, dr2 − dr1) = 0 |
|
|
|
|
||||||||||
или если учесть (166) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
(M1M 2 , dr1 ) − (M1M 2 , dr2 ) = 0 . |
|
(168) |
|||||||||||||
Равенство (168) можно записать так |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| M |
1 |
M |
2 |
|| dr |
| cos α |
1 |
− | M |
1 |
M |
2 |
|
|| dr |
2 |
| cos α |
2 |
= 0 или |
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|dr1| cos α1 − |dr2| cos α2 = 0. |
|
|
(169) |
|||||||||||||
Найдем элементарную работу реакций
(R1 , dr1) + (R2 , dr2) = (R1 , dr1) − (R1 , dr2) =
= R1 |dr1| cos α1 − R1 |dr2| cos α2 = R1 ( |dr1| cos α1 − |dr2| cos α2) = 0.
Таким образом, стержень является идеальной связью.
Заметим, что абсолютно твердое тело можно представлять как совокупность материальных точек , попарно соединенных абсолютно твердыми стержнями. Отсюда следует, что работа внутренних сил на любом перемещении тела равна нулю.
2.Неподвижный цилиндрический шарнир без трения. Пусть
ктелу прикреплен неподвижный цилиндрический шарнир (рис.48). Как известно из курса статики, реакция шарнира проходит через ось
шарнира. Поэтому элементарная работа реакции RO шарнира
dA = (RO , dro) = 0,
так как ось шарнира неподвижна и dro равно нулю. Таким образом, неподвижный цилиндрический шарнир является идеальной связью.
Рис.48 Совершенно аналогично можно доказать, что неподвижный сферический шарнир является идеальной
168

связью.
3. Абсолютно твердая идеально шероховатая поверхность.
Пусть по такой поверхности катится абсолютно твердый каток (рис.49). Так как проскальзывание в точке соприкосновения Р катка и поверхности отсутствует, то перемещение drp точки Р катка равно нулю и работа реакции
dA = (R , drp ) = 0,
т.е. абсолютно твердая идеально Рис.49 шероховатая поверхность явля-
ется идеальной связью.
§3. Принцип возможных перемещений (принцип Лагранжа)
Бесконечно малые перемещения механической системы, допускаемые мгновенно остановленными связями, называются возможными.
Если связи, наложенные на механическую систему стационарны, то возможными являются бесконечно малые перемещения, допускаемые этими связями.
Возможные перемещения точек системы будем обозначать символом δrk (k = 1,2,…,n).
Теорема (принцип возможных перемещений). Для того чтобы механическая система, подчиненная идеальным, стационарным, геометрическим, удерживающим связям, находилась в равновесии, необходимо и достаточно, чтобы скорости точек системы в начальный момент равнялись нулю и сумма элементарных работ активных сил на любом возможном перемещении равнялась нулю, т.е.
n
Vk (0) = 0 (k= 1,2,…,n), δA = ∑(Fk , δrk ) = 0 . (170)
k=1
169
Доказательство.
Необходимость. Вышеуказанная механическая система находится в равновесии, необходимо доказать, что выполнены условия (170). Очевидно, что равенство нулю скоростей выполнено. Убедимся, что выполнено и второе условие (170). Каждая из точек системы находится в равновесии, следовательно, выполнены равенства
Fk + Rk = 0 (k = 1,2,…,n). |
(171) |
Здесь Fk − сумма активных сил, действующих на точку Мk , Rk − сумма реакций связей, приложенных к этой точке. Придадим системе возможное перемещение, при котором каждая из точек получает перемещение δrk . Умножим скалярно каждое из равенств (171) на δrk и просуммируем по всем точкам системы. В результате будем иметь
n |
n |
|
∑(Fk , δrk ) + ∑(Rk , δrk ) = 0 . |
(172) |
|
k=1 |
k=1 |
|
Так как связи, наложенную на систему идеальны, то вторая сумма в
левой части (172) равна нулю, и из (172) следует (170). Достаточность. Допустим, что несмотря на выполнение условий
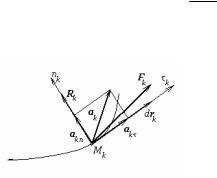
(170), система пришла в движение. При этом каждая из точек получает перемещение drk . Направим ось τk по направлению этого вектора. Так как в начальный момент скорости точек равнялись нулю, а связи, наложенные на систему стационарные и геометрические, то предположение о том, что система пришла в движение означает, что скорость точки Mk начинает возрастать, а следовательно, касательное ускорение точки
akτ = dVkτ > 0. dt
Тогда
(ak , drk ) = (akτ , drk ) > 0. |
(173) |
|
По третьему закону динамики |
|
mk ak = Fk + Rk . |
|
Из (173) следует |
|
(Fk + Rk , drk ) = mk (ak , drk ) > 0. |
Рис.50 |
Суммируя эти равенства по всем |
170
