Курс теоретической механики 2007 (Рус)

точки называется скорость (ускорение) точки относительно подвижной системы координат.

Переносной скоростью Ve (переносным ускорением ae) движущейся точки называется скорость (ускорение) той точки подвижной среды, с которой в данный момент времени совпадает движущаяся точка.

Таким образом, переносная скорость (переносное ускорение) точки М равно скорости (ускорению) точки µ подвижной среды относительно неподвижной системы отсчета:

Ve =Vµ , ae = aµ .

§ 2. Теорема о сложении скоростей

Абсолютная скорость точки равна геометрической сумме ее относительной и переносной скоростей, т.е.

Доказательство.

Будем называть абсолютной траекторию точки относительно неподвижной системы отсчета, а относительной – ее траекторию относительно подвижной системы отсчета (или относительно подвижной среды).

Рассмотрим два положения подвижной среды – в момент времени t и в момент времени t+ t (рис.23). Положение движущейся точки в момент времени t обозначим буквой М, а в момент времени t+ t символом М/.

Пусть в момент времени t движущаяся точка совпадает с точкой µ подвижной среды, а в момент t+ t – с точкой ν этой

вывод, что

Рис.23

81

Вектор MM / соединяет два положения точки относительно неподвижной системы координат, поэтому мы будем называть его

вектором абсолютного перемещения. Вектор µ/ ν соединяет два

положения движущейся точки относительно подвижной среды, поэтому мы его будем называть вектором относительного

где Vµ - скорость точки µ подвижной среды, с которой совпадает точка М в момент времени t. По определению скорость этой точки и является переносной скоростью точки М. Поэтому (60) тождественно (57).

Теорема доказана.

§ 3. Теорема о сложении ускорений (теорема Кориолиса)

Пусть некоторый переменный вектор (вектор-функция) и = и(t) задан в подвижной системе отсчета. Вследствие движения подвижной системы отсчета относительно неподвижной этот вектор будет иметь, вообще говоря, другое аналитическое выражение в неподвижной системе отсчета, а значит, и его производные в подвижной и неподвижной системах отсчета, вообще говоря, тоже будут разными.

Производную переменного вектора в неподвижной системе

82

отсчета будем называть абсолютной и обозначать символом

da u . dt

Производную переменного вектора в подвижной системе отсче-

та будем называть относительной и обозначать символом dr u . dt

Лемма 1 (о связи между абсолютной и относительной производными переменного вектора). Абсолютная производная

переменного вектора равна относительной производной этого вектора, сложен ной с векторным произведением угловой скорости подвижной среды на этот вектор, т.е.

Доказательство. Пусть подвижная система отсчета совершает поступательное движение относительно неподвижной. Тогда приращения и вектора и в обеих системах отсчета будут одинаковыми, а значит, будут одинаковыми и

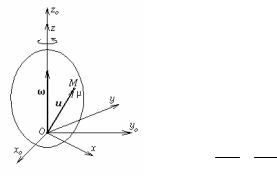
Пусть теперь подвижная среда вращается вокруг неподвижной оси. Направим оси zо и z неподвижной и подвижной систем отсчета вдоль этой оси (рис.25). Движение точки М, положение которой в каждый момент времени определяется радиус-вектором и, будем рассматривать как сложное. Запишем для нее теорему о сложении скоростей:

Вектор и является радиус-вектором точки М, поэтому

83

Переносная скорость точки М равна скорости точки µ подвижной среды, которая определяется по первой формуле Эйлера (52):

Подставляя (64) и (65) в (63), получаем

da u = dr u +[ωe , u] .

dt dt

(62)как частный случай, если положить

ω= 0 при поступательном движении.

Таким образом, лемма доказана.

Лемма 2 (об абсолютной производной переносной скорости).

Абсолютная производная переносной скорости точки по времени равна переносному ускорению, геометрически сложенному с векторным произведением угловой скорости подвижной среды на относительную скорость точки, т.е.

Доказательство. Из определения производной вектор-функции

Здесь µ – точка подвижной среды, с которой совпадает точка М в момент времени t, а ν – точка этой среды, с которой точка М совпадает в момент времени t+ t (рис.26). Отнимем и добавим в числителе

84

Для преобразования первого слагаемого в правой части (68) используем первую формулу Эйлера:

Vν −Vµ' =[ωe , Oν] – [ωe , Oµ/ ] =

=[ωe , Oν − Oµ / ] = [ωe , µ/ ν ]. (69)

положения точки М на относительной траектории – в моменты времени t и t+ t, т.е. он является вектором относительного перемещения.

Поэтому

Воспользовавшись определением производной вектор функции, второе слагаемое в правой части (68) записываем следующим образом:

(так как ускорение точки µ подвижной среды является переносным ускорением точки М).

Таким образом, с учетом (71) и (72) равенство (68) записывается

так

daVe = ае + [ωe , Vr ] , dt

что и требовалось.

Нетрудно доказать, что если переносное движение поступательное,

то

85

daVe = ае .

dt

Как было отмечено в доказательстве предыдущей леммы, можно считать, что этот результат содержится в формуле (66), если при поступательном переносном движении ωe = 0.

Лемма 2 доказана. Введем определение:

кориолисовым ускорением движущейся точки называется

удвоенное векторное произведение угловой скорости подвижной среды на относительную скорость точки:

Теорема о сложении ускорений (теорема Кориолиса).

Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений:

Доказательство. Запишем теорему о сложении скоростей (§2)

и найдем абсолютную производную левой и правой частей равенства (75)

Затем, подставив в формулу (61) вместо и относительную скорость Vr , будем иметь

86

3)полученный вектор Vr/ поворачиваем на 90о в этой плоскости

всторону переносного вращения и умножаем его на 2|ωе|.

Рис.27

§ 6. Пример решения задачи на сложное движение точки

Равнобедренный прямоугольный треугольник АВС вращается из состояния покоя вокруг катета АС с постоянным угловым ускорением ε=1с-2. По стороне АВ движется точка М по закону s=4t3 (м). Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t=2с, если ωο=0.

88

Точка µ треугольника, с которой совпадает точка М в этот момент времени, описывает окружность в плоскости, перпендикулярной оси вращения, радиус

которой h= ssin 450 = 162 м. Скорость точки µ является переносной скоростью точки М и определяется по формуле для скорости точки вращающегося тела:

Ve = ωh .

Угловую скорость вращения треугольника находим из формулы для равноускоренного вращения

ω = εt + ω0 = 2 c−1 ( ω0 = 0) . Тогда Ve = 322 м/с.

Абсолютная скорость точки М равна геометрической сумме относительной и переносной скоростей:

Va = Vr +Ve

и так как угол между Vr и Vе равен 90о , то абсолютная величина Va определяется по формуле

Va = Vr2 +Ve2 = 65,97м/с

Переходим к определению абсолютного ускорения. Так как относительное движение точки М прямолинейное, то нормальное относительное ускорение равно нулю и полное относительное ускорение совпадает с касательным:

ar = ar,τ = dVr = 24t dt

При t=2с получаем ar=48м/с2. Направлено относительное ускорение вдоль стороны АВ.

Переносное ускорение точки М, т.е. ускорение точки µ, состоит из двух составляющих – касательного и нормального ускорений, так как точка µ является точкой равноускоренно вращающегося тела. Касательное переносное ускорение равно

ae,τ = εh = 162 м/с2

инаправлено вдоль касательной к окружности, по которой движется точка µ, а нормальное переносное ускорение равно

ae,n = ω2h = 642 м/с2

89

и направлено вдоль радиуса этой окружности к ее центру.

Для построения кориолисова ускорения используем правило Жуковского. Сначала необходимо спроектировать вектор относительной скорости на плоскость перпендикулярную оси вращения подвижной среды, т.е. на плоскость треугольника АВС. Таковой плоскостью является плоскость окружности, которую описывает точка µ. В результате проектирования Vr на эту плоскость

получаем вектор Vr/ , который направлен вдоль радиуса окружности

плоскости на 90о в сторону вращения треугольника. Таким образом получаем направление вектора кориолисова ускорения ак. Величина кориолисова ускорения определяется так:

ak = 2ωVr/ = 2 2 242 = 962 м/с2

Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений, и так как переносное ускорение само равно сумме касательной и нормальной составляющих, то приходим к следующей формуле:

aa=ar+ae,τ+ae,n+ak

Выберем систему прямоугольных координат следующим образом:

ось y направим параллельно оси вращения; тогда оси x и z будут лежать в плоскости окружности, описываемой точкой µ, причем ось x горизонтальна, а z вертикальна.

Приведенное выше равенство спроектируем на оси координат. В результате получим

aa,x = ae,τ + ak = 1122 м/с2

aa,y = ar cos450 = 242 м/с2

aa,z = ar cos450 − ae,n = −402 м/с2

Тогда модуль абсолютного ускорения может быть найден из формулы

aa = aa2,x + aa2, y + aa2,z = 171,58 м/с2

90