Курс теоретической механики 2007 (Рус)

k=1

n

m&z& = ∑Fk,z (x, y, z, x&, y&, z&,t).

k=1

Если силы, действующие на точку, известны, то выражения в правых частях (11) представляют собой заданные функции своих аргументов, и нахождение уравнений движения

x = f1 (t), y = f2 (t), z = f3 (t)

сводится к интегрированию дифференциальных уравнений (11). Поэтому последовательность решения второй задачи динамики

материальной точки состоит из следующих операций:

1)составление дифференциальных уравнений движения

точки;

2)интегрирование дифференциальных уравнений;

3)определение постоянных интегрирования из заданных начальных условий;

4)нахождение искомых величин и исследование полученных результатов.

§4. Примеры решения второй задачи динамики

1. Прямолинейное движение точки под действием силы, зависящей от времени.

Задача. Тело массой m = 2 кг начинает двигаться из состояния покоя вдоль горизонтальной шероховатой плоскости, коэффициент трения которой равен f = 0.1, под действием силы F = 4t2 (Н). Найти

закон движения тела.

Решение. Выберем начало отсчета в начальном положении тела и направим ось х в сторону движения. Тогда начальные условия движения тела запишутся так:

Рис.3

112

Показываем на чертеже все силы, действующие на тело. Это вес Р, заданная сила F, нормальная реакция поверхности N и сила трения Fтр. Составляем основное уравнение динамики

ma = F+P+N+Fтр

и проектируем его на ось х

Разделив (13) на m и учитывая, что по закону Кулона Fтр = fP, получаем

После подстановки заданных значений m, f и F уравнение (14) принимает следующий вид:

(g принято равным 9,8 м/с2).

Это и есть дифференциальное уравнение движения точки. Умножив его на dt и проинтегрировав, получим

Значение постоянной интегрирования С1 найдем из начальных условий (12), учитывая, что V = Vx = x& = 0 при t = 0. Подставляя это равенство в (16), находим, что С1 = 0. Умножая теперь (16) на dt и интегрируя еще раз, приходим к следующему равенству:

Постоянную интегрирования С2 находим из условия х = 0 при t = 0. Подставляя это в (17), находим, что С2 = 0. Таким образом, уравнение движения тела имеет следующий вид:

x = 1 t 4 − 0.49t 2 . 6

2.Прямолинейное движение точки под действием силы,

зависящей от скорости.

Задача. Некоторое тело массой m = 2 кг опускается внутри гладкой наклонной трубы, заполненной жидкостью, без начальной скорости

113

(рис.4). Полагая, что сила сопротивления жидкости движению груза определяется соотношением R = 0,4V (Н) и пренебрегая выталкивающей силой жидкости, найти скорость тела спустя 10 с после

начала движения.

Решение. Показываем на чертеже силы, действующие на тело, и состав-

Рис.4 ляем основное уравнение динамики точки

Направляем ось х вдоль направления движения и проектируем (18) на эту ось. Учитывая, что V = Vx = x& , находим

Подставляя сюда исходные данные, получаем дифференциальное уравнение:

dV = 4,9 − 0,2V . dt

Это уравнение с разделяющимися переменными. Приводим его к следующему виду:

и интегрируем левую часть по t, а правую по V. В результате будем иметь

Используем начальное условие: V = 0 при t = 0. Из (20) получаем

С = 5 ln 4,9.

Подставим это в (20) и произведем потенцирование:

114

Из (21) следует, что с течением времени V возрастает от нуля постепенно приближаясь 24,5 м/с, но теоретически ни при каком конечном t этого значения не достигает. Поэтому знак абсолютной величины в (21) может быть опущен. В результате получаем

Равенство (22) показывает, что практически уже через несколько секунд после начала движения V неуловимо мало отличается от своего предельного значения. При t =10 с V = 24,5 м/с.

3.Баллистическая задача.

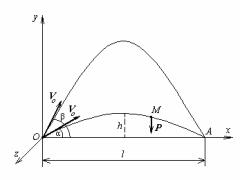
Рассмотрим движение тела (снаряда), выброшенного с начальной скоростью Vo из точки О горизонтальной плоскости под углом α к этой плоскости. Сопротивлением воздуха пренебрегаем, кроме того, будем считать, что сила тяжести снаряда всюду одна и та же, т.е. что высота полета снаряда не очень велика. Необходимо при заданных α и Vo найти дальность полета снаряда l и время его полета Т, а также при заданных Vo и l найти угол выстрела α (т.е. решить задачу

прицеливания).

Решение. Проведем вертикальную плоскость через вектор Vo. В этой плоскости через точку проводим горизонтальную ось Ох и вертикальную ось Оу. Ось Оz проводим перпендикулярно плоскости Оху. На снаряд, который мы считаем материальной точкой, действует только одна сила тяжести. Поэтому основное уравнение динамики выглядит так:

Проектируя его на оси координат, получаем

115

Умножим равенства (24) на dt и проинтегрируем:

Начальные условия задачи выглядят так:

x = 0, y = 0, z = 0, Vx = Vo cos α, Vy = Vo sin α, Vz = 0 при t = 0. (26)

Из (25) и последних трех равенств (26) следует

C1 = Vo cos α, C2 = Vo sin α, C3 = 0.

Тогда (25) запишется так:

x& = Vo cos α, y& = Vo sin α− gt, z& = 0 .

Умножая эти равенства на dt и интегрируя, находим

x = Vo t cos α +C4, y = Vo t sin α − gt2 / 2 + C5, z = C6 . (27)

Подставляя сюда значения x, y и z из первых трех равенств (26) и t= 0,

получаем, что

С4 = С5 = С6 = 0.

При этих значениях произвольных постоянных равенства (27) представляют собой уравнения движения снаряда:

Последнее равенство означает, что снаряд движется в плоскости Оху.

1. Найдем уравнение траектории снаряда. Для этого необходимо исключить время t из первых двух уравнений (28):

116

gx2

y = x tg α − . (29) 2Vo2 cos2 α

Таким образом, снаряд, выпущенный под углом к горизонту, при отсутствии сопротивления воздуха движется по параболе.

2.Определим горизонтальную дальность полета снаряда.

Для этого в уравнении (29) положим у = 0. Не совпадающая с началом координат точка траектории с такой ординатой имеет абсциссу

g

3. Определим время полета снаряда. Для этого в первом равенстве (28) положим х равным правой части (30). В результате будем иметь

4.Осталось решить задачу прицеливания. Заметим, что из (30)

следует , что максимальная дальность полета снаряда достигается при α = 45о:

постоянно направленная к неподвижному центру О и пропорциональная расстоянию от материальной точки М до

этого центра, т.е.

117

( c – положительная постоянная).

Подобная сила создается растянутой или сжатой пружиной (рис.6). Здесь lo − длина недеформированной пружины. При смещении груза от точки О в любую сторону пружина стремится вернуть груз в исходное положение, при этом упругая сила пружины F пропорциональ-

Рис.6 на величине смещения ОМ с коэффициентом пропорциональ-

ности с, носящим название коэффициента жесткости пружины.

Прямолинейное движение материальной точки под действием только одной восстанавливающей силы называется свободными колебаниями Точка О (центр восстанавливающей силы)

называется центром колебаний.

Заметим, что центр колебаний является положением равновесия точки М. Действительно, в соответствии с формулой (31), если материальная точка М находится в положении О, то F оказывается равной нулю, и на точку М в этом положении вообще не действуют силы.

Проведем ось Ох из центра колебаний вдоль прямой, по которой движется точка (рис.7). Составим основное уравнение динамики точки

ma = F

и спроектируем его на ось х, учитывая, что проекция восстанавливающей силы равна

В результате будем иметь

Разделив (32) на m и введя обозначение

получаем дифференциальное уравнение свободных колебаний

материальной точки

118

Это линейное однородное дифференциальное уранение второго порядка с постоянными коэффициентами. Составим его характеристи-

ческое уравнение :

λ2 + k2 = 0.

Так как кони его чисто мнимые λ1,2 = ± ικ, то общее решение дифференциального уравнения (34) имеет следующий вид:

x = C1 sin kt + C2 cos kt.

Выражение (35) представляет собой уравнение свободных колебаний материальной точки.

Прямолинейное движение точки, совершаемое по закону x = a sin (kt + α), называется гармоническими колебаниями.

Таким образом, свободные колебания материальной точки

являются гармоническими.

Величина а, являющаяся наибольшим отклонением точки от

центра колебания, называется амплитудой.

Величина φ = kt + α называется фазой колебания, а α = φ (0)

называется начальной фазой.

Величина k называется круговой или циклической частотой

колебаний.

Промежуток времени Т, в течение которого точка совершает

одно полное колебание, называется периодом колебаний.

Это означает, что если время в формуле (35) увеличивается на Т, то аргумент синуса в этой формуле изменяется на 2π. Отсюда следует,

т.е. круговая частота равна числу полных колебаний, совершаемых

119

за 2π единиц времени.

Число ν полных колебаний, совершаемых в единицу времени,

1)амплитуда и начальная фаза колебаний зависят от начальных условий,

2)круговая частота и период не зависят от них.

§6. Влияние постоянной силы на свободные колебания материальной точки

Пусть теперь на материальную точку помимо восстанавливающей силы действует еще постоянная сила Р (рис.8).

Найдем новое положение равновесия О1 точки М. Очевидно, в этом положении F + P = 0, т.е.

120