
Курс теоретической механики 2007 (Рус)
.pdf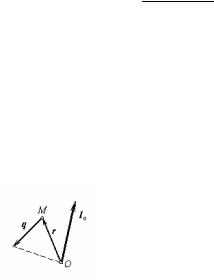
Vг = V1 + V, |
(94) |
где V1 − относительная скорость груза, а V − искомая скорость призмы. Количество движения механической системы определяется по формуле
Q = m1Vг + m2V = m1 (V1 + V) + m2V. |
(95) |
Проектируя равенство (95) на ось х и используя (93), получаем
m1 V1 cos 30o − (m1 + m2) V = 0,
откуда находим
V = m1V1 cos300 = 0,29 м/с m1 + m2
§6. Теорема об изменении кинетического момента материальной точки
Кинетическим моментом lo материальной точки относительно полюса О называется момент вектора q количества
движения точки относительно этого полюса:
lo = mo (q). |
(96) |
Момент вектора количества движения относительно полюса определяется аналогично моменту силы относительно полюса (см. §4 главы I части I). Поэтому для кинетического момента имеет место следующее представление:
Рис.24 |
lo = [r , q], т.е. |
(97) |
кинетический момент точки относительно полюса равен векторному произведению радиус-вектора точки на ее количество движения.
141
Кинетическим моментом lz материальной точки относительно оси z называется момент вектора q количества
движения точки относительно этой оси:
lz = mz (q). |
(98) |
Момент вектора количества движения относительно оси определяется аналогично моменту силы относительно оси (см. §3 главы I части I).
Между кинетическими моментами относительно полюса и оси существует зависимость, аналогичная зависимости между моментами силы относительно полюса и оси (см. §8 главы I части I):
lz = прz l o , |
(99) |
т.е. кинетический момент точки относительно оси, проходящей
через полюс, равен проекции на эту ось кинетического момента точки относительно полюса.
Теорема (об изменении кинетического момента точки относительно полюса). Геометрическая производная
кинетического момента материальной точки относительно полюса по времени равна главному моменту сил, приложенных к точке, относительного этого полюса:
|
|
|
|
|
|
|
dt |
n |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
dlo |
= |
|
|
mo (Fk ) . |
(100) |
||||||||
|
|
|
|
|
|
|
|
|
k=1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Продифференцируем формулу (97) по времени |
|||||||||||||||||||
|
dlo |
= |
d |
[r, mV ] = [ |
dr |
, mV ]+[r, m |
dV |
] . |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
dt |
dt |
|
|
|
dt |
|
dt |
|||||||||||
Пользуясь тем, что |
|
dr |
=V , |
|
dV |
= a , а |
также тем, что векторное |
||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
dt |
|
dt |
|
|
|
||||||||||
произведение двух коллинеарных векторов равно нулю, получаем |
|||||||||||||||||||
|
|
|
|
|
|
|
|
dlo |
|
= [r, ma] . |
(101) |
||||||||
|
|
|
|
|
|
|
|
dt |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Используем теперь третий закон динамики и подставим равенство
n
ma = ∑Fk
k=1
в формулу (101):
142
|
dlo |
|
n |
|
n |
|
|
= |
∑ |
[r, F ] = |
∑ |
m (F ) . |
|
|
|
|||||
|
dt |
k |
o k |
|||
|
|
|
|
|
||
|
|
|
k=1 |
|
k=1 |
|
Теорема доказана. |
|
|
|
|
||
§7. Теорема об изменении кинетического момента механической системы
Кинетическим моментом механической системы относительно полюса называется вектор, приложенный в этом полюсе и равный геометрической сумме кинетических моментов точек системы относительно этого полюса:
n |
|
Lo = ∑lok |
(102) |
k=1
(lok = mo(qk) − кинетический момент точки Мk механической системы относительно полюса О).
Кинетическим моментом |
механической системы относи- |
||
тельно оси |
называется скаляр, |
равный сумме |
кинетических |
моментов точек системы относительно этой оси: |
|
||
|
n |
|
|
|
Lz = ∑lzk |
(103) |
|
|
k=1 |
|
|
(lzk = mz(qk) |
− кинетический момент точки Мk |
механической |
|
системы относительно оси z).
Пользуясь соотношением (99), легко доказать следующее утверждение:
кинетический момент механической системы относительно оси, проходящей через полюс, равен проекции на эту ось кинетического момента механической системы относительно полюса, т.е.
Lz = прz L o |
(104) |
Теорема (об изменении кинетического момента механической системы относительно полюса). Геометрическая производная
кинетического момента механической системы относительно полюса по времени равна главному моменту внешних сил, приложенных к системе, относительно этого полюса:
143

dLo |
= Moe . |
(105) |
|
||
dt |
|
|
Доказательство. Для каждой из точек механической системы может быть записана теорема об изменении кинетического момента относительно полюса (рис.25)
dlok |
= mo (Fke ) + mo (Fki ) (k =1,2,..., n) . |
(106) |
|
||
dt |
|
|
Суммируя равенства (106) по k, получаем
n |
dlok |
= |
n |
mo (Fke ) + |
|
|
∑ |
||
∑ dt |
|
|||
k=1 |
|
|
k=1 |
|
n
+ ∑mo (Fki ). k=1
Меняя местами дифференцироРис.25 вание и суммирование и учитывая, что главный момент внут-
ренних сил относительно любого полюса равен нулю, получаем (105). Теорема доказана.
Следствия.
1)Внутренние силы не влияют на изменение кинетического момента механической системы относительно полюса.
2)(закон сохранения кинетического момента) Если главный момент внешних сил относительно полюса равен нулю в течение некоторого промежутка времени, то кинетический момент механической системы относительно этого полюса не изменяется ни по величине, ни по направлению в течение указанного промежутка.
Доказательство. Если M oe = 0, то из теоремы следует, что
dLo = 0 , а значит, Lo = const. dt
3) (теорема об изменении кинетического момента механической системы относительно оси). Производная кинетического момента механической системы относительно оси по времени равна сумме моментов внешних сил, приложенных к системе, относительно этой оси:
144
n
dLz = ∑mz (Fke ) . (107) dt r=1
Доказательство. Запишем равенство (105) в следующем виде:
dLo |
|
n |
|
|
= |
∑ |
mo (Fke ) |
||
|
||||
dt |
|
|||
|
|
k=1 |
|
|
и спроектируем его на ось z. Пользуясь формулой (104), а также зависимостью между моментами силы относительно полюса и оси, получаем (107).
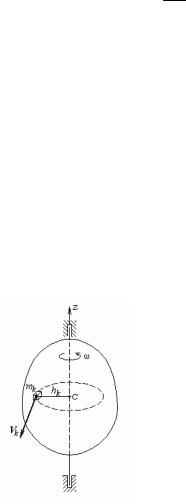
§8. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси
Рассмотрим твердое тело, вращающееся вокруг неподвижной оси (рис.26). Мысленно разобьем тело на элементарные объемы (элементарные массы). Одна из таких элементарных масс показана на рисунке. Количество движения такой элементарной массы равно
qk = mk Vk ,
|
а кинетический момент относительно оси z: |
|
|
lzk = qk hk = mk Vk hk . |
(108) |
|
Скорость точки вращающегося |
тела |
|
определяется по формуле |
|
|
Vk = ωhk . |
|
|
Подставив это в (108), будем иметь |
|
|
lzk = mk ω hk2 . |
(109) |
Рис.26 |
Суммируя (109) по всем элементарным мас- |
|
|
сам, образующим тело, получим формулу |
|
для кинетического момента твердого тела, вращающегося вокруг неподвижной оси, относительно оси вращения
n |
|
Lz = ω∑mk hk2 . |
(110) |
k=1
145

Введем обозначение
n |
|
J z = ∑mk hk2 |
(111) |
k=1
иназовем Jz моментом инерции тела относительно оси z. Таким образом, моментом инерции тела относительно оси называется
сумма произведений элементарных масс, образующих тело, на квадрат их расстояний от оси.
Тогда (110) запишется так
Lz = Jz ω, |
(112) |
т.е. кинетический момент тела, вращающегося вокруг
неподвижной оси, относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость вращения.
§9. Моменты инерции некоторых тел
1.Полый цилиндр.
Будем называть полым цилиндр, масса которого распределена по его поверхности.
Так как масса цилиндра распределена по его поверхности, то элементарные массы расположены также на его поверхности (рис.27) и расстояние их от оси одинаково и равно радиусу цилиндра R. Тогда
n |
|
J z = ∑mk R2 = MR2 . |
(113) |
k=1
(М − масса цилиндра).
Рис.27
2.Сплошной однородный цилиндр.
Выделим из сплошного цилиндра полый цилиндр радиуса r < R , толщина стенок которого бесконечно мала и равна dr (рис.28). Его
момент инерции dJz может быть вычислен по формуле (113) dJz = dM r2.
146

Здесь dM − масса полого цилиндра. Ее нетрудно определить следующим образом: находим сначала плотность цилиндра
|
ρ = |
|
M |
|
|
||
|
πR2H |
|
|||||
|
|
|
|||||
|
(М − масса сплошного цилиндра, R − его |
||||||
|
радиус, Н − высота). Затем находим объем |
||||||
|
полого цилиндра |
|
|
|
|
|
|
|
dV = 2πrdrH. |
|
|||||
|
Тогда |
|
|
|
|
|
|
|
dM = ρdV = |
2Mrdr |
, |
||||
|
R2 |
||||||
|
|
|
|
|
|||
Рис.28 |
dJz = |
|
2Mr3dr |
|
|||
|
|
. |
|
||||
|
|
||||||
|
|
|
R2 |
|
|||
Будем полагать, что сплошной цилиндр состоит из бесконечного множества вложенных друг в друга полых цилиндров, радиусы которых меняются от 0 до R . Тогда
R |
|
|
|
R |
|
|
3 |
|
|
J z = ∫dJ z |
= ∫ |
2Mr |
dr . |
||||||
2 |
|
||||||||
0 |
|
|
0 |
|
R |
|
|
||
|
|
|
|
|
|
|
|||
После интегрирования получаем |
|
|
|
|
|
|
|
||
J |
|
= |
MR2 |
. |
|
(114) |
|||
z |
|
|
|||||||
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|||
3.Стержень.
Определим момент инерции прямолинейного однородного стержня
|
относительно |
оси, |
|
перпендикулярной стержню и |
|
|
проходящей через один из его |
|
|
концов (рис.29). |
|
|
Выделим элемент |
стержня |
|
длиной dx, находящийся на |
|
|
расстоянии х от оси z. Его масса |
|
Рис.29 |
равна: |
|
dM = M dx l
(М − масса стержня, l − его длина). Тогда
147

J = |
∑ |
x |
2dM = l |
Mx2 |
dx . |
|
l |
||||||
z |
|
∫ |
|
|||
|
|
|
|
|
||
|
|
|
0 |
|
|
После интегрирования получаем
J = |
M l 2 |
. |
(115) |
z |
3 |
|
§10. Моменты инерции относительно параллельных осей (теорема Гюйгенса – Штейнера)
Теорема. Момент инерции Jz тела относительно некоторой оси z равен моменту инерции тела Jz’ относительно z’, проходящей
через центр масс тела параллельно данной оси, сложенному с произведением массы тела на квадрат расстояния между осями:
Jz = Jz’ + Мd2. |
(116) |
Доказательство. Выделим элементарную массу mk тела (рис.30). Обозначим через hk расстояние от элементарной массы до оси z, а че-
рез hk/ - расстояние от нее до оси z’. Используя теорему косинусов,
можно записать |
|
|
|
|
|
|
(hk)2 = (hk/ )2 |
+ d 2 |
− 2d hk/ |
cos α . |
|
|
Но h/ cos α = y/ , где y/ |
- ордината |
|||
|
k |
k |
k |
|
|
|
массы mk , т.е. |
|
|
|
|
|
(hk)2 = (hk/ )2 |
+ d 2 |
− 2d yk/ . (117) |
|
|
|
Умножим (117) |
на |
mk |
и |
|
|
просуммируем по всем элементарным |
|
|||
|
массам, образующим тело. В резуль- |
|
|||
Рис.30 |
тате получим |
|
|
|
|
n
Но ∑mk
k=1
J z = J z'
n
равно массе тела М, а ∑mk yk/
k=1
nn
+d 2 ∑mk − 2d∑mk yk/ .
k=1 |
k=1 |
= M yC/ = 0 по формуле (75)
148

для ординаты центра масс, причем ось y’ проходит через центр масс С. Таким образом, имеем
Jz = Jz’ + Мd2,
что совпадает с (116).
§11. Пример решения задачи с применением теоремы об изменении кинетического момента механической системы
Задача. На однородный барабан массой m1 = 10 кг и радиусом r = 0,5 м (рис.31) намотана веревка с грузом массой m2 = 5 кг на конце. Пренебрегая массой веревки и трением на оси барабана, определить угловое ускорение барабана.
Решение. Ось z вращения барабана перпендикулярна плоскости чертежа и проходит через центр барабана О. Применим теорему об изменении кинетического момента механической системы относительно оси z, полагая, что механическая система состоит из барабана и груза, внешними силами по отношению к которой являются вес барабана
Р1 , вес груза Р2 и реакция оси барабана R :
|
|
dLz |
= P r . |
(118) |
|
|
|
||
|
|
dt |
2 |
|
|
|
|
|
|
кинетический момент системы состоит из |
||||
кинетического |
момента |
барабана, |
||
определяемого по формуле |
|
|||
Рис.31 |
|
L(z1) |
= J z ω, |
|
и кинетического момента груза |
|
|||
lz(2) |
= m2V2 r . |
|
|
|
Момент инерции барабана как однородного цилиндра определяется следующим образом:
|
m r 2 |
|
J z = |
1 |
, |
|
||
2 |
|
|
а скорость груза можно выразить через угловую скорость барабана
149

|
V2 = ω r. |
|
||
Тогда |
|
|
|
|
Lz |
= L(z1) + lz(2) = ( |
m1 |
+ m |
2 ) r 2ω. |
|
||||
|
2 |
|
|
|
Подставив это в (118), будем иметь
(m1 + m2 )r 2 dω = m2 gr , 2 dt
откуда находим
ε = |
m2 g |
= 9,8 с−2 . |
|
(m1 + m2 )r
2
§12. Работа силы
Напомним, что элементарным перемещением точки (см. §5 главы I
части II) называется бесконечно малый вектор |
|
dr = Vdt, |
(119) |
направленный по касательной к траектории точки. Из (119) следует, что
|dr| = V dt = ds,
т.е. длина элементарного перемещения точки равна бесконечно малому отрезку дуги траектории.
Элементарной работой силы F (т.е. работой силы на элементарном перемещении dr) называется скалярная величина
dA = F ds cos α , |
(120) |
где α − угол между направлением силы и касательной к траектории (рис.32). Заметим, что (120) может быть записано и так
dA = Fτ ds , |
(121) |
|
так как проекция силы F на |
направление |
касательной равна |
Fτ = F cos α. Кроме того, из (119) следует |
|
|
dA = F |dr| cos α = (F, dr), |
(122) |
|
150
