
Прикладна механіка_ЛЕКЦІЇ
.pdf
|
|
|
|
71 |
|
|
|
|
|
точок |
A |
і |
B |
опускаємо на цю площину перпендикуляри, отримуючи на |
площині проекцію Pxy . Отриману проекцію можна розкласти на складові
Px і Py . Тепер визначимо момент сили P відносно осі |
z |
(за теоремою |
Варіньона), як суму моментів, що створюють складові |
Px |
і Py відносно |
точки O . Як бачимо з рисунка, цей момент дорівнює |
|
|
mz
Py
x Px
y
.
(1.58)
Рис. 1.31
Таким же чином можна визначити моменти сили P відносно двох інших осей. Для визначення моменту сили P відносно осі x необхідно спроектувати її на площину yOz . Отриману проекцію розкласти на

72
складові Pz і Py і визначити момент сили |
P |
моментів її складових відносно точки O : |
|
mx Pz y Py z . |
|
І, нарешті, відносно осі y : |
|
відносно осі
x
, як суму
(1.59)
my Px z Pz x .
Таким чином, значення моментів сил визначаються виразами:
(1.60)
m |
x |
yP |
zP |
, |
|
z |
y |
|
|
m |
y |
zP |
xP |
, |
|
x |
z |
|
|
m |
z |
xP |
yP . |
|
|
y |
x |
||
(1.61)
Тобто, для розрахунку моменту сили відносно координатних осей необхідно задати координати точки прикладання сили і проекції сили на осі координат.
§ 4.6. Головний вектор і головний момент просторової
системи довільних сил
Подібно до плоскої системи просторову систему довільно розташованих сил можна звести до любої точки простору. Порядок зведення такий самий, як і для плоскої системи довільно розташованих сил, при цьому від кожної сили отримаємо силу і пару сил в центрі зведення.
Таким чином, будь-яка просторова система довільних сил, що діє на тіло, може бути зведена до однієї сили – головного вектора системи і однієї пари – головного моменту системи просторових сил.

73
Головним вектором називається геометрична сума
P |
P |
гл. |
1 |
просторової всіх сил даної
P |
... P |
|
2 |
n |
|
системи системи:
n
Pk . k 1
довільних сил
(1.62)
Проекції головного вектора просторової системи довільних сил на
координатні осі |
x, y,z |
можна визначити аналітичним способом, як |
алгебраїчну суму проекцій всіх сил системи ці осі:
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
P |
P |
P |
... P |
|
|
P |
, |
|
|
гл.x |
1x |
2 x |
3 x |
nx |
|
|
kx |
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
P |
P |
P |
... P |
|
n |
|
|
|
|
P |
P |
|
, |
|||||||
гл.y |
1 y |
2 y |
3 y |
ny |
|
|
ky |
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
P |
P |
P |
... P |
|
|
n |
|
|
|
P |
|
P . |
|
|
||||||
гл.z |
1z |
2 z |
3 z |
nz |
|
kz |
|
|
||
|
|
|
|
|
|
k 1 |
|
|
|
|
(1.63)
Тоді модуль головного вектора просторової системи довільних сил визначається через його проекції як діагональ паралелепіпеда,
побудованого на цих проекціях:
|
|
n |
|
2 |
|
n |
|
2 |
|
n |
|
2 |
|
Pгл. |
|
|
|
|
|||||||||
|
Pkx |
|
|
Pky |
|
|
Pkz . |
(1.64) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
k 1 |
|
|
k 1 |
|
|
|
|||
На відміну від плоскої системи сил моменти сил просторової системи відносно центру зведення діють в різних площинах.
Тому головний момент просторової системи довільно розташованих сил визначається як геометрична сума моментів всіх сил системи відносно центра зведення:
n |
|
M гл. m1 m2 ... mn mk . |
(1.65) |
k 1

74
Проекції головного моменту просторової системи довільних сил на координатні осі x, y,z , що проходять через дану точку зведення системи,
можна визначити аналітично як алгебраїчну суму моментів всіх сил системи відносно цих осей x, y,z :
|
|
|
P |
m |
P |
m |
P |
... m |
|
P |
|
|
n |
|
|
P |
|
, |
|
||||
M |
гл.x |
m |
|
|
|
m |
|
|
|||||||||||||||
|
x |
1 |
x |
2 |
x |
|
3 |
|
x |
|
n |
|
|
|
x |
|
k |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
m |
P |
m |
P |
m |
|
P |
|
... m |
|
|
P |
n |
|
|
|
P |
|
||||
M |
гл.y |
|
|
y |
|
m |
|
, |
|||||||||||||||
|
y |
1 |
y |
2 |
y |
3 |
|
n |
|
y |
|
k |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
P |
m |
P |
m |
P |
... m |
|
P |
|
|
n |
|
|
P |
|
. |
|
||||
M |
гл.z |
m |
|
|
m |
|
|
||||||||||||||||
|
z |
1 |
z |
2 |
z |
|
3 |
|
z |
|
|
n |
|
|
z |
|
k |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
(1.66)
Абсолютне значення головного моменту заданої системи сил відносно центра зведення системи через знайдені проекції дорівнює:
|
|
|
|
n |
|
|
2 |
|
n |
|
|
2 |
|
n |
|
|
2 |
M |
|
|
m |
|
m |
|
m |
|
|||||||||
гл. |
|
|
P |
|
|
|
P |
|
|
|
P |
|
|||||
|
|
|
x |
k |
|
|
y |
k |
|
|
z |
k |
|
||||
|
|
|
k 1 |
|
|
|
k 1 |
|
|
|
k 1 |
|
|
|
|||
. (1.67)
Слід відмітити, що у загальному випадку головний вектор |
R не |
|
залежить від положення центра зведення |
O , а головний момент |
M , |
навпаки, залежить від його положення, |
тому що змінюються плечі |
|
"приєднаних" пар, або плечі заданих сил відносно центра зведення.
§ 4.7. Умови рівноваги тіла, що перебуває під дією
просторової системи довільних сил
Оскільки будь-яку просторову систему довільних сил можна звести до однієї сили – головного вектора Pгл. та однієї пари – головного моменту
M гл. , які прикладені до тіла, то для рівноваги тіла необхідно і достатньо,

75
щоб головний вектор нулю:
Pгл.
і головний момент
P |
|
0, |
|
|
гл. |
|
|
|
|
M |
|
|
|
|
гл. |
0. |
|||
|
|
|
||
M гл.
одночасно дорівнювали
(1.68)
M гл.
Причому,
0 |
то M гл.x |
якщо
0, M
P |
|
0 |
гл. |
|
|
гл.y |
0 |
|
|
|
|
,
і
то
M гл.z
Pгл.x
0
0
.
,
Pгл.y 0 і
Pгл.z
0
,
а якщо
Проекції головного вектора системи координат дорівнюють:
Pгл.
на осі просторової декартової
|
|
n |
|
|
|
|
|
|
|
P |
|
P |
, |
|
гл.x |
|
kx |
|
|
|
|
k 1 |
|
|
|
|
n |
|
|
P |
P |
, |
||
гл.y |
|
ky |
|
|
|
|
k 1 |
|
|
|
|
n |
|
|
P |
P . |
|
||
гл.z |
|
kz |
|
|
|
|
k 1 |
|
|
Проекції головного моменту на ці ж осі координат дорівнюють:
n |
|
|
|
M гл.x mx |
Pk , |
||
k 1 |
|
|
|
n |
|
|
|
M гл.y my Pk , |
|||
k 1 |
|
|
|
n |
|
|
|
M гл.z mz |
Pk . |
||
k 1 |
|
|
|
(1.69)
(1.70)
Тоді, з урахуванням (1.68) та (1.69), вираз (1.70) можна остаточно подати у вигляді аналітичних рівнянь рівноваги тіла під дією просторової системи довільних сил:

76
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
0, |
|
||
kx |
|
|
|
|||
k 1 |
|
|
|
|
|
|
n |
P |
|
|
0, |
|
|
|
|
|
||||
ky |
|
|
|
|||
k 1 |
|
|
|
|
|
|
n |
|
|
|
|
|
|
kz |
0, |
|
||||
|
P |
|
|
|||
k 1 |
|
|
|
|
|
|
n |
|
|
P |
|
|
|
|
|
|
0, |
|||
|
m |
x |
|
|||
|
k |
|
|
|||
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
P |
|
|
|
|
|
|
0, |
|||
|
m |
y |
|
|||
|
k |
|
|
|||
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
m |
|
P |
|
|
|
|
|
0. |
||||
|
|
z |
k |
|
|
|
k 1 |
|
|
|
|
|
|
(1.71)
На підставі цих рівнянь складаються конкретні рівняння рівноваги тіл під дією просторової системи, що складається із зовнішніх сил і реакцій в’язей.
Таким чином, для рівноваги тіла, яке перебуває під дією просторової системи довільних сил, необхідно і достатньо, щоб алгебраїчні суми проекцій всіх сил на осі просторової декартової системи координат і алгебраїчні суми моментів всіх сіл відносно цих осей дорівнювали нулю.
§ 4.8. Умови рівноваги тіла, що перебуває під дією
просторової системи паралельних сил
Якщо сили, що прикладені до тіла, розташовані у просторі, але паралельні, то можна вибрати систему координат так, щоб одна з осей
(наприклад, вісь z ) була паралельна даним силам (рис. 1.32ё). Тоді дві інші осі x, y будуть утворювати площину, яка буде перпендикулярною цим силам. Проекції заданих сил на осі x та y дорівнюють нулю. Задані сили

77
також не створюють моментів відносно осі осі.
Рис. 1.32
z
, так як вони паралельні цій
Тоді для просторової системи паралельних сил три умови рівноваги з загальної системи рівнянь рівноваги (1.71) випадають, а залишаються три інші. Отже, для рівноваги просторової системи паралельних сил маємо наступні рівняння рівноваги:
n |
|
|
|
Pkz 0, |
|
|
|
k 1 |
|
|
|
n |
|
|
|
mx |
Pk 0, |
(1.72) |
|
k 1 |
|
|
|
n |
|
|
|
my |
Pk |
0. |
|
k 1 |
|
|
|
Таким чином, для рівноваги тіла, що перебуває під дією просторової системи паралельних сил, необхідно і достатньо, щоб алгебраїчна сума проекцій всіх сил на вісь, яка паралельна силам, і алгебраїчні суми моментів відносно двох інших осей дорівнювали нулю.

78
§ 4.9. Теорема Варіньона про момент рівнодійної сили
відносно осі
|
Розглянемо |
тіло під |
|
дією |
просторової системи |
довільних |
|
сил |
||||||||||
1, 2 , |
3 |
,..., n , що зведена до рівнодійної |
R , яка прикладена до тіла в точці |
|||||||||||||||
P P |
P |
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C (рис. 1.33). Прикладемо до цієї точки |
C |
зрівноважувальну силу R |
|
, яка |
||||||||||||||
|
|
|||||||||||||||||
по модулю дорівнює рівнодійній силі |
|
|
і розташована з нею на одній |
|||||||||||||||
R |
||||||||||||||||||
прямій, але має протилежний напрямок. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
У |
цьому випадку |
тіло |
під |
дією |
системи |
сил |
1 , 2 , |
3 ,... |
|
n |
і |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P P |
P |
|
,P |
|
|
зрівноважувальної |
сили |
R |
|
, |
буде |
знаходитись у |
стані |
рівноваги. |
Це |
|||||||||
|
||||||||||||||||||
означає, що алгебраїчна сума моментів всіх цих сил відносно будь-якої осі декартової системи координат повинна дорівнювати нулю.
Запишемо дану умову рівноваги спочатку відносно осі |
x : |
n |
|
P |
m |
R |
|
m |
|||
x |
k |
x |
|
|
k 1 |
|
|
|
|
0
.
(1.73)
Рис. 1.33

79
Знайдемо з цього виразу момент сили дорівнювати:
R
відносно осі
x
. Він буде
|
|
|
|
n |
|
|
|
|
mx Pk . |
|
(1.74) |
||
mx R |
|
|||||
|
|
|
|
k 1 |
|
|
Оскільки модуль сили |
R |
|
дорівнює модулю |
сили |
R , але |
|
|
||||||
протилежний за напрямком, то |
R R . Це означає, що |
mx R mx R . |
||||
Підставимо значення цього моменту у (1.74) і матимемо: |
|
|
||||
mx R |
|
|
n |
|
|
|
mx Pk . |
|
(1.75) |
||||
|
|
|
|
k 1 |
|
|
Такі умови можна скласти відносно двох інших осей.
Теорема доведена.
Таким чином, якщо просторова система довільних сил зводиться до рівнодійної, то момент рівнодійної сили відносно довільної осі дорівнює алгебраїчній сумі моментів складових сил відносно цієї ж осі.
§ 4.10. Приклад рівноваги тіла під дією просторової системи
довільних сил
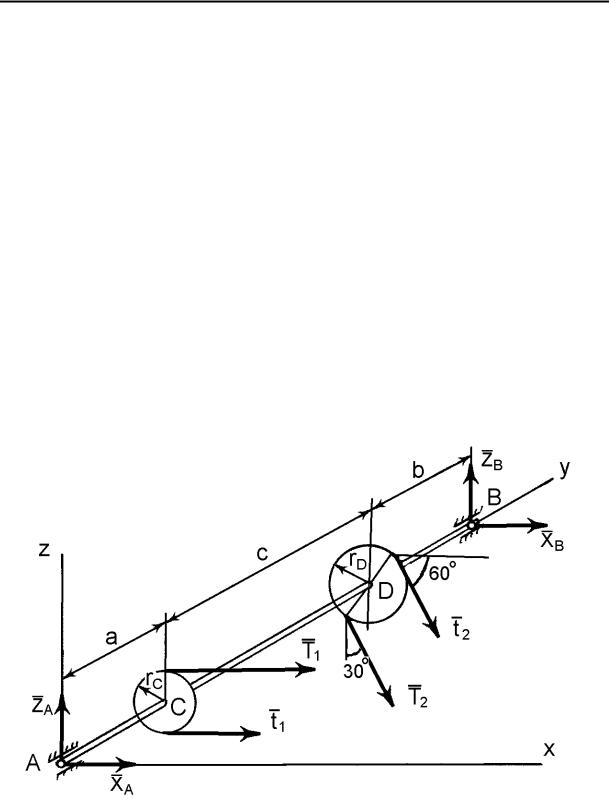
Горизонтальний вал трансмісії (рис. 1.34) несе пасової передачі і може обертатися у підшипниках A
дорівнюють rC = 0,2 м , rD = 0,25 м . Натяги гілок
два |
шківи C |
і |
D |
і B . Радіуси шківів |
|||
паса |
на шківі |
C |
– |
горизонтальні T1
і |
t1 |
, причому, T1 2t1 = 4905 Н . Натяги гілок паса на
шківі D
– |
T2 |
і
t2
, причому,
T2
2t2
, із вертикаллю вони утворюють кут
30o . Розміри вала дорівнюють:
перебуває у рівновазі.
a
= b = 0,5
м
,
с
= 1
м
. Система
80
Визначити натяги
T2
і
t2
та реакції підшипників
A
і
B
.
Розв'язання |
|
|
|
|
|
Розглянемо рівновагу вала |
AB |
із шківами |
C |
і |
D . Звільнимо вал від |
в'язей, замінивши їх відповідними реакціями. У підшипниках реакції
розташовані у площині, яка |
перпендикулярна до осі вала AB . Таким |
чином, реакції підшипників A |
і B розташовані відповідно у площині xAz |
та у площині, що паралельна до неї і проходить крізь точку B . Невідомий
вектор кожної реакції підшипників у площині визначається двома проекціями на осі x і z , як це показано на рис. 1.34. Після зроблених припущень, отримана просторова система довільних сил, що перебуває у стані рівноваги.
Рис. 1.34
