Прикладна механіка_ЛЕКЦІЇ

11

Рис. 1.4

Таким чином, ІІІ аксіома статики дає можливість геометрично додати дві сили, що прикладені в одній точці

З курсу геометрії відомо, що діагональ паралелограма, тобто модуль рівнодійної, дорівнює

V аксіома встановлює, що не існує односторонньої дії сили.

Два взаємодіючих тіла діють одне на одне з рівними за модулем, але протилежними за напрямком силами.

Ця аксіома носить назву закону дії та протидії.

Слід зауважити, що сили взаємодії ніколи не зрівноважуються, тому що вони прикладені до різних тіл.

§1.3. Вільне і невільне тіло. В'язі та їх реакції

Утеоретичній механіці тверді тіла і матеріальні системи поділяються на вільні та невільні.

Тіло вважається вільним, якщо воно має можливість рухатись у

12

просторі в будь – якому напрямку і невільним – якщо рух його у просторі чимось обмежується.

Тіла, або перешкоди, що обмежують рух даного тіла, називаються

в'язями. Вважається, що на невільне тіло накладені в'язі.

Механічна дія в'язі на дане тіло називається реакцєюї в'язі. У статиці

розглядаються найпростіші в'язі у формі різних твердих та гнучких тіл.

Розглянемо основні типи в'язей як розрахункові моделі. Кожна з цих

в'язей має свою назву, графічне зображення і свої реакції.

нормалі. Гладенька площина накладає одну в'язь – неможливість рухатись по нормалі від поверхні, тому буде одна реакція, яка напрямлена проти напрямку втраченого переміщення за рахунок накладення в'язі.

крізь центри сфер О і О1 по нормалі п (перпендикулярно до дотичної ).

по перпендикуляру до лінії (поверхні) тіла, яке утримується в даній точці.

3. Шарнірно – нерухома опора або нерухомий шарнір (підшипник) (рис. 1.5, в). Реакція шарнірно – нерухомої опори прикладена у центрі шарніра і заздалегідь невідома за напрямком. Невідомий вектор реакції розкладається на дві складових вздовж осей координат Rx і Ry . З другого боку, ця опора накладає дві в'язі – неможливість вертикального і горизонтального переміщень, тому і буде дві відповідні складові реакції у площині, яка перпендикулярна до осі шарніра.

4. Шарнірно – рухома опора або коток (рис. 1.5, г). Реакція цієї в'язі

R спрямована перпендикулярно до площини, по якій рухається коток.

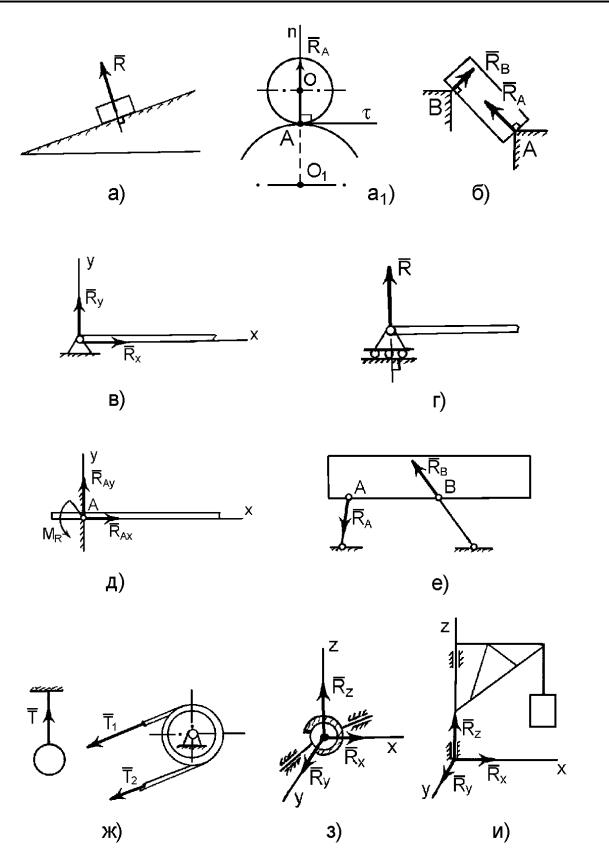
13

Рис. 1.5

14

5. Жорстке закріплення (рис. 1.5, д). Реакція цієї в'язі представлена складовими у вигляді сил RAx , і RAy та моменту реакції M R . Це відповідає кількості в'язей, які накладає ця опора: неможливість вертикального і

горизонтального лінійних переміщень та повороту у площині.

6. Ідеальний стержень, тобто невагомий тонкий стержень, на кінцях якого встановлені циліндричні, точкові шарніри і який працює тільки на розтяг або на стиск (рис. 1.5, е). Реакція цієї в'язі R спрямована вздовж

стержня і прикладена у центрі шарніра.

7. Гнучка нитка або в'язь, яка здійснюється ідеальними гнучкими тілами, тобто невагомими, нерозтяжними нитками: канатами, пасами,

ланцюгами (рис. 1.5, ж). Реакція цієї в'язі T напрямлена вздовж нитки і прикладена у точці закріплення А. У пасовій передачі натяги в її гілках T1 і

T2 також вважаються реакціями гнучких в'язей.

8. Сферичний шарнір або його частковий випадок – підп'ятник

(рис. 1.5, з, и). Реакція цієї в'язі зображена трьома складовими у вигляді

підп'ятника.

У зв'язку з введенням поняття в'язей вводиться VI та VII аксіоми статики, які носять назви аксіоми про звільнення від в'язей та аксіоми про накладання нових в'язей.

VІ аксіома. Рівновага невільного матеріального тіла не порушиться якщо відкинути в'язі, що накладені на нього, а замість них прикласти сили,

які дорівнюють їх реакціям.

VІІ аксіома. Рівновага невільного матеріального тіла не порушиться якщо на нього накласти нові в'язі.

16

попередньої сили (рис.1.6). Тоді вектор рівнодійної з'єднує початок першої сили з кінцем останньої сили. Це можна записати так:

Тобто, рівнодійна плоскої системи збіжних сил дорівнює векторній сумі цих сил і є замикаючою стороною силового багатокутника,

побудованого на векторах сил цієї системи.

Величина рівнодійної сили не зміниться, якщо буде змінено порядок приєднання (додавання) сил до багатокутника, але конфігурація силового багатокутника буде іншою.

§1.5. Умова рівноваги плоскої системи збіжних сил

угеометричній формі

Якщо до вільного матеріального тіла прикладена одна сила певної величини, то про рівновагу цього тіла мови бути не може. Тобто, якщо розглядати плоску систему збіжних сил, яка зведена до рівнодійної, то тіло не може бути у рівновазі.

Тільки у випадку, коли рівнодійна системи дорівнює нулю (рис. 1.7),

ця система буде знаходитись у стані рівноваги.

Таким чином, для рівноваги тіла під дією плоскої системи збіжних сил необхідно і достатньо, щоб рівнодійна всіх сил дорівнювала нулю.

Ця умова виражається векторним рівнянням:

або скорочено:

17

Рівнодійна такої системи сил буде дорівнювати нулю, коли силовий багатокутник буде замкненим, тобто коли початок вектора першої сили буде співпадати з кінцем вектора останньої сили.

Рис. 1.7

Геометричну умову рівноваги можливо застосовувати при розв’язанні деяких задач статики графічним методом. При цьому:

1)вибирають тіло, рівновагу якого будуть розглядати;

2)відкидають в’язі, замінюючи їх реакціями;

3)користуючись умовою рівноваги, будують замкнений силовий багатокутник і визначають невідомі величини (у більшості випадків – це реакції в’язей).

Розв’язання задач на рівновагу за допомогою графічної побудови силових багатокутників має певні незручності, пов’язані з відкладанням векторів на площині і точністю отриманих результатів. Доцільніше при розв’язанні таких задач користуватись не геометричною, а аналітичною умовою рівноваги, яка базується на методі проекцій сил на осі координат.

18

§ 1.6. Проекція сили на осі координат

Проекцією сили на вісь – називається напрямлений відрізок на осі,

утворений між перпендикулярами, які опущені із початку і кінця вектора сили на цю вісь.

Правило знаків для проекції наступне:

якщо напрямок проекції сили на вісь співпадає з позитивним напрямком осі, то така проекція буде додатною, якщо ні – то від’ємною.

Рис. 1.8

19

Цілком зрозуміло, якщо цей кут дорівнює 90о , то проекції Px =0,

Py = P . Тобто, сила, яка направлена паралельно осі, проектується на цю

вісь в натуральну величину, а її проекція на перпендикулярну вісь дорівнює нулю.

можна визначити його проекції на осі координат.

Але справедливим буде і зворотне ствердження. По величині

а також його напрямок.

Модуль сили P , як діагональ прямокутника, побудованого на його проекціях, визначається з наступного виразу:

Знаючи напрямні косинуси, через арккосинуси можна знайти і самі

кути.

20

§ 1.7. Визначення рівнодійної плоскої системи збіжних сил

аналітичним способом

дорівнює векторній сумі цих сил і є замикаючою стороною силового багатокутника, побудованого на векторах сил цієї системи (рис. 1.9).

напрямлені відрізки, які і є проекціями всіх сил на цю вісь. Кожна проекція, відповідно, дорівнює: