
big_doc_LKG
.pdf


|
|
|
Випадкові процеси та їх статистичні характеристики |
181 |
|||||||||
|
|
|
|
|
|
|
; |
......................................... |
|
|
; |
|
|
|
|
|
|
|
|
|
; |
|
|
|
. |
|
|
|
Отримані таким чином результати представлені в табл. 3.9. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Таблиця 3.9 |
||
|
|
Результати обчислень нормованої кореляційної функції |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
1 |
|
0,74 |
0,81 |
0,72 |
0,76 |
0,65 |
0,74 |
0,53 |
0,81 |
1,00 |
|
2 |
|
|
1 |
0,92 |
0,99 |
0,94 |
0,91 |
0,86 |
0,77 |
0,89 |
0,89 |
|
|
3 |
|
|
|
1 |
0,94 |
0,91 |
0,95 |
0,98 |
0,90 |
0,92 |
0,91 |
|
|
4 |
|
|
|
|
1 |
0,96 |
0,96 |
0,76 |
0,82 |
0,92 |
0,84 |
|
|
5 |
|
|
|
|
|
1 |
0,94 |
0,89 |
0,72 |
0,99 |
0,89 |
|
|
6 |
|
|
|
|
|
|
1 |
0,97 |
0,90 |
0,93 |
0,83 |
|
|
7 |
|
|
|
|
|
|
|
1 |
0,94 |
0,91 |
0,84 |
|
|
8 |
|
|
|
|
|
|
|
|
1 |
0,70 |
0,71 |
|
|
9 |
|
|
|
|
|
|
|
|
|
1 |
0,81 |
|
|
Для отримання середніх значень нормованої кореляційної функції (останній стовпець табл. 3.9) необхідно знайти суму значень діагональних елементів матриці  вздовж паралелей головної діагоналі і поділити її на кількість елементів в цій діагоналі:
вздовж паралелей головної діагоналі і поділити її на кількість елементів в цій діагоналі:
;
;
;
..................................................................................
 ;
;  .
.
Обчислені середні значення нормованої кореляційної функції  занесемо до табл. 3.9 та побудуємо графіки (рис. 3.6) емпіричних характеристик процесу доставки вантажів.
занесемо до табл. 3.9 та побудуємо графіки (рис. 3.6) емпіричних характеристик процесу доставки вантажів.

182 |
Розділ 3 |
Рис. 3.6. |
Графіки характеристик випадкового процесу доставки вантажів |
Проаналізуємо отримані результати з точки зору передбачуваної стаціонарності випадкового процесу  . Судячи із графіків, можна зробити висновок, що випадковий процес
. Судячи із графіків, можна зробити висновок, що випадковий процес  не є стаціонарним, так як
не є стаціонарним, так як  не має постійного значення, дисперсія
не має постійного значення, дисперсія  змінюється у часі, значення нормованої кореляційної функції
змінюється у часі, значення нормованої кореляційної функції  уздовж паралелей головної діагоналі також мають різні значення.
уздовж паралелей головної діагоналі також мають різні значення.
Однак, приймаючи до уваги дуже обмежену кількість реалізацій ( ), ці видимі відхилення від стаціонарності можна враховувати несуттєвими. Тому цілком доцільним буде припущення про стаціонарність випадкового процесу
), ці видимі відхилення від стаціонарності можна враховувати несуттєвими. Тому цілком доцільним буде припущення про стаціонарність випадкового процесу  .
.
Метод Фостера-Стюарта.
Цей метод дає можливість визначити стаціонарність за середніми і дисперсією. Реалізація методу здійснюється за чотири етапи.
На першому етапі виконується порівняння випадкової функції у кожному перерізі, починаючи з другого, із всіма попередніми. При цьому визначаються дві числові послідовності:

Випадкові процеси та їх статистичні характеристики |
183 |
де  – дискретні моменти часу.
– дискретні моменти часу.
На другому етапі розраховуються величини  і
і  :
:
; |
. |
(3.17) |
Величина  характеризує змінювання функції і приймає значення від 0 (всі значення функції однакові між собою) до
характеризує змінювання функції і приймає значення від 0 (всі значення функції однакові між собою) до  (функція змінюється монотонно). Величина
(функція змінюється монотонно). Величина  характеризує змінювання дисперсії значень функції і змінюється від
характеризує змінювання дисперсії значень функції і змінюється від  (функція монотонно спадає) до
(функція монотонно спадає) до  (функція монотонно зростає).
(функція монотонно зростає).
Третій етап полягає у перевірці таких гіпотез:
1)випадковості відхилення величини  від математичного очікування
від математичного очікування  ;
;
2)випадковості відхилення величини  від нуля.
від нуля.
Ця перевірка виконується з використанням розрахункових значень t-критерію Стьюдента для середнього та для дисперсії :
 ;
;  . (3.18)
. (3.18)
При  значення
значення 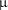 та
та  приймаються за табл. 3.10.
приймаються за табл. 3.10.
Таблиця 3.10 Значення 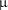 та
та  критерію Фостера-Стюарта
критерію Фостера-Стюарта
|
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
1,964 |
2,153 |
2,279 |
2,373 |
2,447 |
2,509 |
2,561 |
2,606 |
2,645 |
|
1,288 |
1,521 |
1,677 |
1,791 |
1,882 |
1,956 |
2,019 |
2,072 |
2,121 |
При  величини
величини  та
та  обчислюються за формулами
обчислюються за формулами


Випадкові процеси та їх статистичні характеристики |
185 |
Необхідно перевірити вантажопотік на стаціонарність.
Розв’язок.
1. Розраховуємо (табл. 3.12) величини  ,
,  і знаходимо
і знаходимо  і
і  .
.
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 3.12 |
|
|
|
|
Результати розрахунку значень |
, , |
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
76 |
– |
– |
– |
– |
26 |
92 |
|
1 |
|
0 |
1 |
1 |
2 |
78 |
1 |
0 |
1 |
1 |
27 |
94 |
|
1 |
|
0 |
1 |
1 |
3 |
79 |
1 |
0 |
1 |
1 |
28 |
99 |
|
1 |
|
0 |
1 |
1 |
4 |
77 |
0 |
0 |
0 |
0 |
29 |
98 |
|
0 |
|
0 |
0 |
0 |
5 |
76 |
0 |
0 |
0 |
0 |
30 |
100 |
|
1 |
|
0 |
1 |
1 |
6 |
75 |
0 |
1 |
1 |
–1 |
31 |
97 |
|
0 |
|
0 |
0 |
0 |
7 |
75 |
0 |
0 |
0 |
0 |
32 |
94 |
|
0 |
|
0 |
0 |
0 |
8 |
73 |
0 |
1 |
1 |
–1 |
33 |
95 |
|
0 |
|
0 |
0 |
0 |
9 |
74 |
0 |
0 |
0 |
0 |
34 |
100 |
|
0 |
|
0 |
0 |
0 |
10 |
74 |
0 |
0 |
0 |
0 |
35 |
104 |
|
1 |
|
0 |
1 |
1 |
11 |
74 |
0 |
0 |
0 |
0 |
36 |
113 |
|
1 |
|
0 |
1 |
1 |
12 |
65 |
0 |
1 |
1 |
–1 |
37 |
111 |
|
0 |
|
0 |
0 |
0 |
13 |
66 |
0 |
0 |
0 |
0 |
38 |
114 |
|
1 |
|
0 |
1 |
1 |
14 |
67 |
0 |
0 |
0 |
0 |
39 |
110 |
|
0 |
|
0 |
0 |
0 |
15 |
71 |
0 |
0 |
0 |
0 |
40 |
109 |
|
0 |
|
0 |
0 |
0 |
16 |
71 |
0 |
0 |
0 |
0 |
41 |
115 |
|
1 |
|
0 |
1 |
1 |
17 |
67 |
0 |
0 |
0 |
0 |
42 |
119 |
|
1 |
|
0 |
1 |
1 |
18 |
73 |
0 |
0 |
0 |
0 |
43 |
123 |
|
1 |
|
0 |
1 |
1 |
19 |
81 |
1 |
0 |
1 |
1 |
44 |
119 |
|
0 |
|
0 |
0 |
0 |
20 |
88 |
1 |
0 |
1 |
1 |
45 |
123 |
|
0 |
|
0 |
0 |
0 |
21 |
90 |
1 |
0 |
1 |
1 |
46 |
131 |
|
1 |
|
0 |
1 |
1 |
22 |
89 |
0 |
0 |
0 |
0 |
47 |
147 |
|
1 |
|
0 |
1 |
1 |
23 |
89 |
0 |
0 |
0 |
0 |
48 |
151 |
|
1 |
|
0 |
1 |
1 |
24 |
85 |
0 |
0 |
0 |
0 |
49 |
147 |
|
0 |
|
0 |
0 |
0 |
25 |
91 |
1 |
0 |
1 |
1 |
50 |
141 |
|
0 |
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
∑ |
22 |
16 |
2. За табл. 3.10 для  знаходимо:
знаходимо:
 ;
;  ;
;
3. Використовуючи формули (3.18), обчислюємо статистики для випадкових величин r і d:


Випадкові процеси та їх статистичні характеристики |
187 |
або
, (3.20)
де  – середній ранг для кожної випадкової величини
– середній ранг для кожної випадкової величини  ;
;
 – середній ранг за всією послідовністю.
– середній ранг за всією послідовністю.
Якщо всі  мають один і той же закон розподілу, то
мають один і той же закон розподілу, то 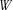 набуває невеликих значень, при різних законах розподілу
набуває невеликих значень, при різних законах розподілу  (тобто при від-
(тобто при від-
сутності стаціонарності)  набуває великих значень.
набуває великих значень.
При збігу законів розподілу випадкової величини  статистика
статистика  має
має  -розподіл з кількістю ступенів вільності
-розподіл з кількістю ступенів вільності  . Для
. Для
перевірки стаціонарності (однаковості розподілів випадкових величин  ) необхідно:
) необхідно:
1)задатися рівнем значимості  (зазвичай 0,05 або 0,01);
(зазвичай 0,05 або 0,01);
2)за таблицею  -розподілу для рівня значимості
-розподілу для рівня значимості  та кількості ступенів вільності
та кількості ступенів вільності  знайти квантиль
знайти квантиль  розподілу;
розподілу;
3)якщо 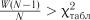 , то гіпотезу щодо стаціонарності слід відхилити і вважати потік вимог нестаціонарним.
, то гіпотезу щодо стаціонарності слід відхилити і вважати потік вимог нестаціонарним.
Приклад 4. Аналізується робота транспортної системи металургійного комбінату. В табл. 3.13 наведені статистичні дані кількості повідомлень  з вузлової станції про прибуття вантажів на адресу підприємства, що надійшли погодинно за 10 год. (
з вузлової станції про прибуття вантажів на адресу підприємства, що надійшли погодинно за 10 год. (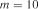 ) робочого часу (з 8:00 до 18:00 год.) за три доби (
) робочого часу (з 8:00 до 18:00 год.) за три доби ( ).
).
Таблиця 3.13
Статистичні дані про кількість повідомлень
Доба |
|
|
Погодинна кількість повідомлень |
|
|
|
|||||
(реалізація) |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
2 |
5 |
5 |
0 |
5 |
6 |
|
4 |
2 |
4 |
2 |
1 |
3 |
5 |
8 |
4 |
3 |
3 |
|
2 |
4 |
2 |
3 |
2 |
4 |
1 |
5 |
7 |
2 |
8 |
|
6 |
8 |
7 |
Для обґрунтування виду математичної моделі потоку повідомлень необхідно перевірити його на стаціонарність.
Розв’язок.
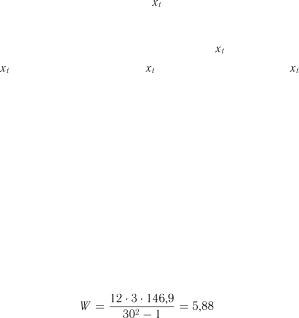

 . Наприклад,
. Наприклад, ;
; ;
; .
. ;
;

 -критерію Стьюдента за прийнятим рів-
-критерію Стьюдента за прийнятим рів- і
і  .
. і
і  .
. знаходяться
знаходяться  та
та  .
. і
і  .
. в залежності від вибраного рівня
в залежності від вибраного рівня ) і кількості ступенів вільності
) і кількості ступенів вільності  .
. і
і  , то процес вважається
, то процес вважається  і
і  , то процес вважається
, то процес вважається  ;
; і
і  , то процес вважається
, то процес вважається  навіть приблизно не може вважатися стаціонарним;
навіть приблизно не може вважатися стаціонарним; і
і  , то процес вважається
, то процес вважається  ) за час перебування транспортних засобів в наряді
) за час перебування транспортних засобів в наряді 
 ;
; .
. і для кількості ступенів вільності
і для кількості ступенів вільності  знаходимо критичне значення
знаходимо критичне значення  .
. і
і  , то процес вважаємо
, то процес вважаємо  мають
мають  (
( ).
). випадкових величин в
випадкових величин в  реалізаціях необхідно:
реалізаціях необхідно: значень
значень  випадкової величини
випадкової величини чисел є
чисел є  однакових, то кожному із них присвоюється ранг, який дорівнює
однакових, то кожному із них присвоюється ранг, який дорівнює  ;
; спостережень величин
спостережень величин  (
( );
); (табл. 3.15). Значення рангу для
(табл. 3.15). Значення рангу для  дорівнює
дорівнює ; для
; для  :
:  і т. д. Отримаємо
і т. д. Отримаємо . Із таблиці квантилей розподілу
. Із таблиці квантилей розподілу  (додаток Д3) для кількості ступенів вільності
(додаток Д3) для кількості ступенів вільності  знаходимо
знаходимо  .
. .
. , то потік повідомлень вважаємо
, то потік повідомлень вважаємо