Mat_Analiz_Prokhorov

Рассмотрим случай f (x0) > 0. В случае f (x0) < 0 рассуждения симметричны. Запишем определение бесконечной малости функции

> 0 > 0 x x0 x x0 < (x) <

и положим = f (x0)/2 > 0. Тогда для всех x x0, x x0 < , справедливо неравенство

f ' '(x0 ) (x), 2

которое вместе с предыдущим неравенством приводят к выводу, что для таких x f(x) f(x0) > 0,

что означает минимальность значения f(x0) среди остальных значений f(x) в -окрестности точки x0 и заканчивает доказательство теоремы 4.

181

Лекция 18

1. Выпуклые множества

2. Выпуклые функции

3. Критерий выпуклости функции

4. Точка перегиба функции

5. Необходимое условие точки перегиба

1. Выпуклые множества

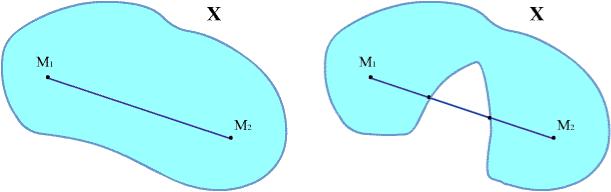
Дадим геометрическое определение выпуклого множества на плоскости.

Определение 1. Множество X R2 называется выпуклым, если отрезок, соединяющий произвольные точки M1 X и M2 X, целиком содержится в Х.

Как известно из курса аналитической геометрии, всякая прямая на плоскости задается линейным уравнением. То же относится к отрезкам на прямой.

182

Если = 0, то M = M2, а если = 1, то M = M1. Когда пробегает значения от 0 до 1, точка М пробегает все точки отрезка M1M2 от M2 до M1.

Рис. 3. Иллюстрация задания отрезка внутри множества линейным уравнением

Векторное линейное уравнение (1) можно записать в координатах. Пусть OM 1,OM 2 и OM имеют координаты (x1, y1), (x2, y2) и (x, y). Тогда векторное уравнение (1) эквивалентно системе двух координатных уравнений в параметрическом виде

0 1.

183

Рис. 4. Иллюстрация задания отрезка внутри множества в параметрическом виде

2. Выпуклые функции

Применим геометрическое определение выпуклого множества к функциям на отрезке, используя понятие графика и выпуклости множества, расположенного выше графика. Сначала формально определим понятие графика функции.

Определение 2. Пусть функция y = f(x) определена на отрезке [a, b]. Тогда множество {(x, y): a x b, y = f(x)} точек на плоскости называется графиком функции y = f(x) на [a, b].

Теперь определим множество, расположенное выше графика функции.

Определение 3. Пусть функция y = f(x) определена на отрезке [a, b]. Тогда множество {(x, y): a x b, y f(x)} точек на плоскости называется надграфиком функции y = f(x) на [a, b].

184

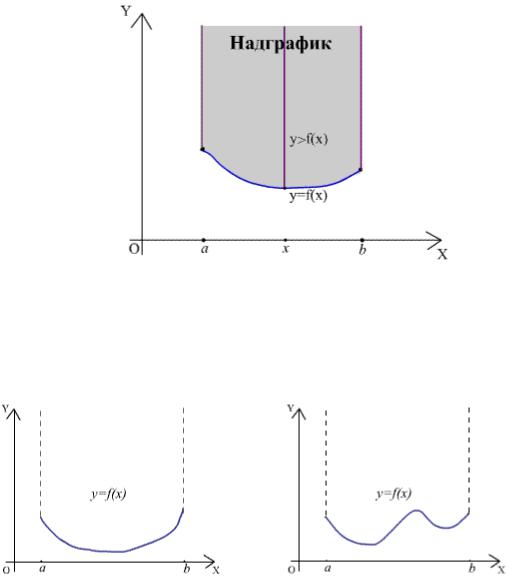
Рис. 5. Надграфик функции.

Выпуклые функции определим как функции с выпуклым надграфиком.

Определение 4. Пусть функция y = f(x) определена на отрезке [a, b] и ее надграфик является выпуклым множеством. Тогда функция f называется выпуклой на [a, b].

Рис. 6. Пример выпуклой функции Рис. 7. Пример невыпуклой функции

Таким образом, функция y = f(x) выпукла, если отрезок, соединяющий любые две точки M1 и M2 ее надграфика, целиком содержится в надграфике. Покажем, что для проверки выпуклости надграфика функции достаточно установить

185

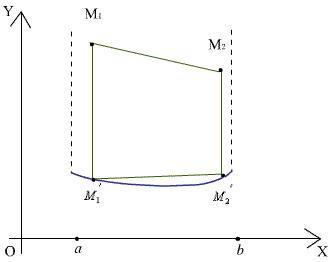
справедливость следующего условия: отрезок, соединяющий любые две точки M 1 и M 2 ее графика, целиком содержится в надграфике.

Рис. 8. Иллюстрация критерия выпуклости надграфика функции

Действительно, выберем в надграфике произвольно точки M1 и M2 и найдем их проекции M 1 и M 2 на график функции. Если

отрезок M 1M 2 содержится в надграфике, то и трапеция M 1M1M2M 2 вместе со стороной M1M2 также содержится в надграфике.

Следовательно, определение 4 эквивалентно следующему определению.

Определение 5. Пусть функция y = f(x) определена на отрезке [a, b]. Эта функция называется выпуклой, если отрезок, соединяющий любые две точки ее графика, расположен не ниже той части графика, которую он стягивает.

Отрезок, соединяющий две точки графика, называется хордой графика. Все определения 1-5 сформулированы геометрически. Однако определение 5 допускает адекватное аналитическое выражение.

186

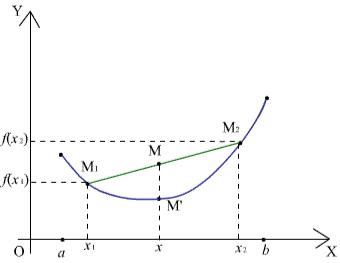
Рис. 9. Иллюстрация определения выпуклой функции

Действительно, пусть функция y = f(x) выпукла. Выберем произвольно точки x1, x2 [a, b], x1 < x2. Тогда точки M1 с

координатами (x1, f(x1)) и M2 с координатами (x2, f(x2)) принадлежат графику функции. Выберем произвольно точку x [x1, x2]. Согласно (2) x можно представить в виде

x= x1 + (1 - )x2

снекоторым параметром [0, 1]. На графике функции точке x соответствует точка M с координатами

( x1 + (1 - )x2, f( x1 + (1 - )x2)).

Кроме того, на хорде, соединяющей M1 и M2, согласно (2) точке x соответствует точка M с координатами ( x1 + (1 - )x2, f(x1) + (1 - )f(x2)).

Тот факт, что точки M и M находятся на одной вертикальной прямой, причем M находится не ниже M , выражается аналитическим неравенством

f( x1 + (1 - )x2) f(x1) + (1 - )f(x2).

187

Следовательно, геометрические определения 4 и 5 эквивалентны следующему аналитическому определению.

Определение 6. Пусть функция f определена на отрезке [a, b]. Эта функция называется выпуклой, если для любых x1, x2 [a, b], x1 < x2, и любого [0, 1] выполняется неравенство

3. Критерий выпуклости функции

Аналитическое определение 6 выпуклости функции на отрезке позволяет применить средства дифференциального исчисления для ее исследования.

Теорема 1. (Критерий выпуклости дифференцируемой функции).

Пусть функция f дифференцируема на отрезке [a, b]. Эта функция является выпуклой тогда и только тогда, когда ее производная f не убывает на [a, b].

Доказательство. Зафиксируем произвольно точки x1, x2 [a, b] и обозначим

( ) = f( x1 + (1 - )x2).

Очевидно, что

Функция является композицией линейной функции относительно и дифференцируемой на [x1, x2] функции f. Поэтому дифференцируема на [0, 1] и ее производная вычисляется по формуле

Докажем сначала необходимость теоремы 1. Предположим, что функция f выпукла на отрезке [a, b], и докажем, что f не убывает. Используя функцию , перепишем неравенство (3) в виде

188

Вычитая (0) из обеих частей неравенства (6) и деля на x1 - x2 < 0, получим

( ) (0) (1) (0) f (x1 ) f (x2 )

Правая часть последнего неравенства не зависит от , а предел при 0 левой части равен (0). Поэтому(0) f(x1) - f(x2)

и ввиду (5) после деления на x1 - x2 < 0 получаем неравенство

(7) f '(x2 ) f (x1) f (x2 ) . x1 x2

Аналогично, вычитая (1) из обеих частей неравенства (6) и деля на x1 - x2 < 0 получим

( ) (1) (1) (0) f (x1 ) f (x2 ).

1

Правая часть последнего неравенства не зависит от , а предел при 1 левой части равен (1). Поэтому

Сравнение (7) и (8) приводит к заключению, что для всех x1, x2 [a, b], x1 < x2, справедливо неравенство f (x1) f (x2),

которое означает, что f не убывает на [a, b]. Теперь докажем достаточность теоремы. Предположим, что f не убывает на [a, b] и докажем, что f выпукла. Выберем (0, 1) и применим к функции на отрезке [0, ] теорему Лагранжа, согласно которой существует точка 1 (0, ) такая, что

(9)

189

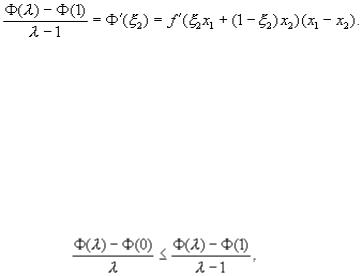
Аналогично применим к функции на отрезке [ , 1] теорему Лагранжа, согласно которой существует точка 2 ( , 1) такая, что

(10)

Поскольку

0 < 1 < < 2 < 1,

то

1x1 + (1 - 1)x2 2x1 + (1 - 2)x2,

и из монотонности f следует, что

f( 1x1 + (1 - 1)x2) f( 2x1 + (1 - 2)x2). Умножая последнее неравенство на x1 - x2 < 0, из (9) и (10) выводим неравенство

которое после элементарных преобразований приводит к неравенству( ) (1) + (1 - ) (0),

эквивалентному (3). Следовательно, функция f выпукла на [a, b], что заканчивает доказательство теоремы 1.

Следствие 1. Пусть функция f дважды дифференцируема на отрезке [a, b]. Эта функция является выпуклой тогда и только тогда, когда для всеx [a, b] справедливо неравенство f (x) 0.

Доказательство. Утверждение следует из того, что производная f дважды дифференцируемой функции f не убывает тогда и

только тогда, когда f (x) 0. В случае дифференцируемых функций дадим другую геометрическую интерпретацию выпуклости.

190